Chapter 6

These are functions with degrees higher than 2

What are polynomial functions?

These are functions with a degree of 3

f(x)=ax³+bx²+cx+d

What are cubic functions?

These are functions with a degree of 4

f(x)=ax^4 +bx³ +cx²+dx+e

What are quartic functions?

These are points on Poly functions where the curve is increasing or decreasing. Also called turning points

What are local extrema points?

This is a point where the curve changes decreasing to increasing

What are local minimum point?

This a point where the curve changes from increasing to decreasing

What is a local maximum point?

This is the highest point on an interval

What is the absolute maximum point?

This is the lowest point on a graph over an interval

What is the absolute minimum point?

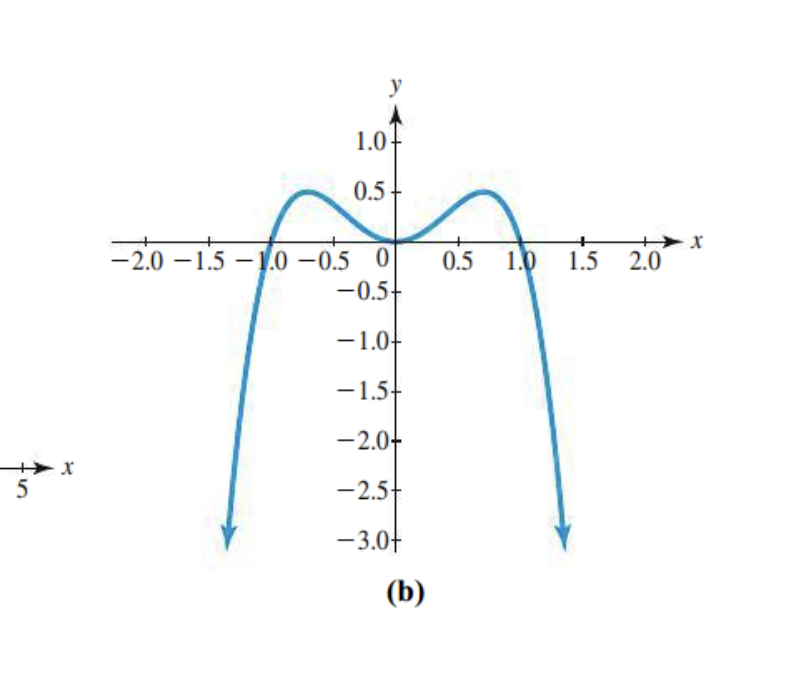
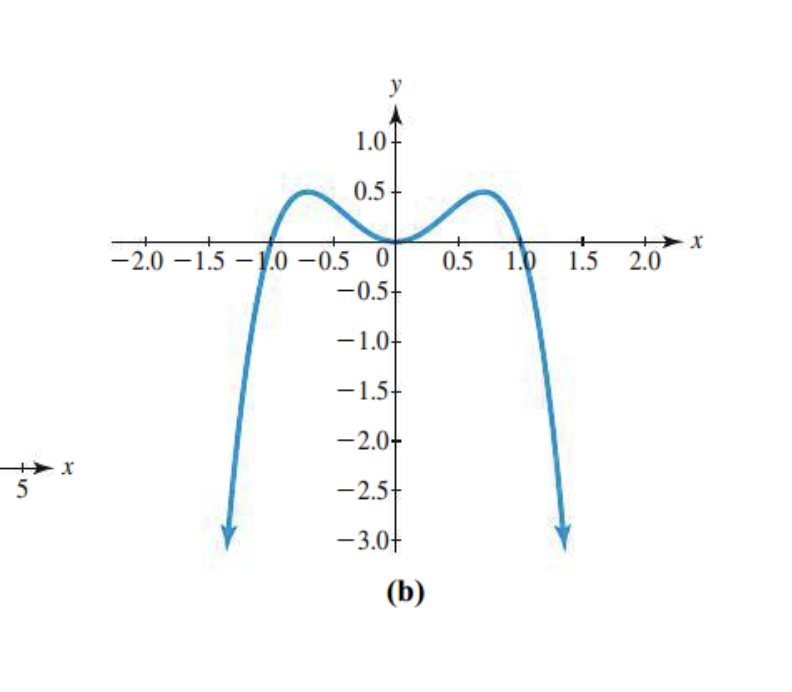
These are functions with either 0 or 2 turning points and the end behavior is one opening up and the other opening down

What are cubic functions?

These are functions with either 1 or 3 turning points and the end behavior is both opening up or opening down.

What are quartic functions?

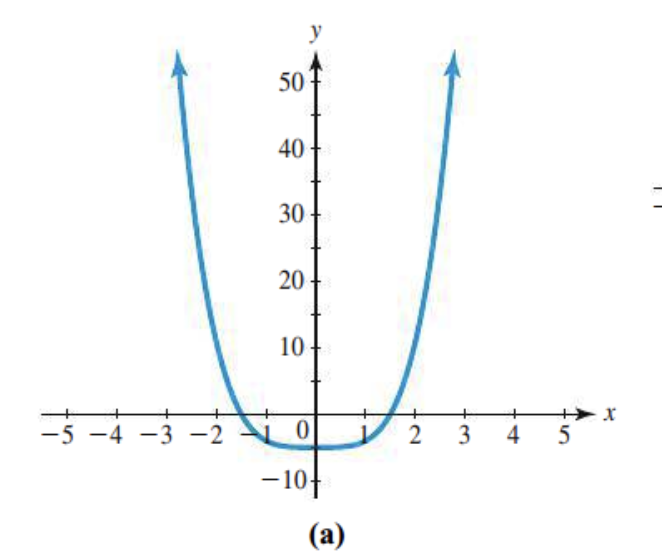
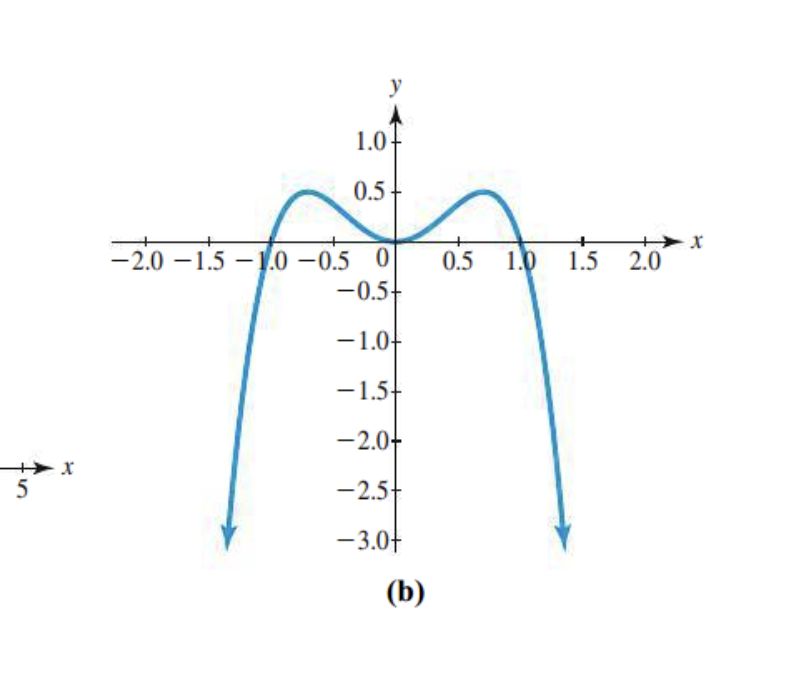
The number of x-intercepts

There are two x-intercepts that are crossing the graph

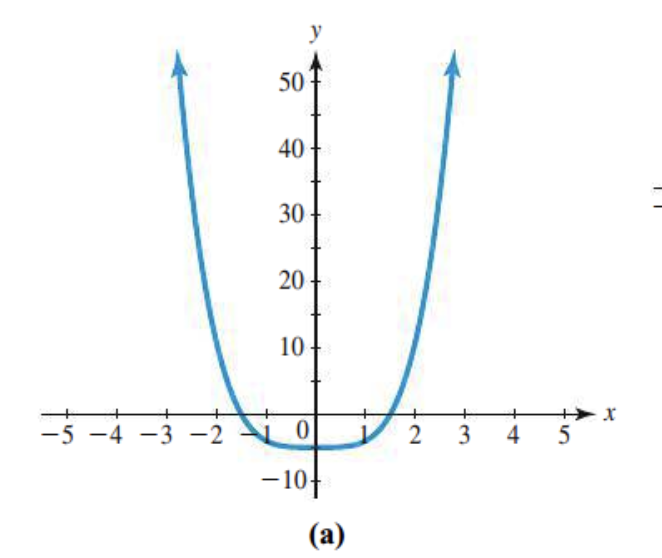
Number of turning points

Only 1, its going from decrease to increasing

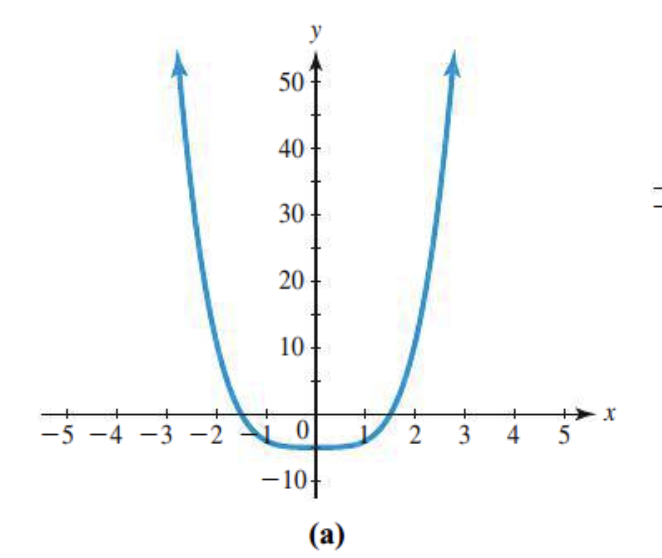
Leading coefficient?

Finish up- Positive

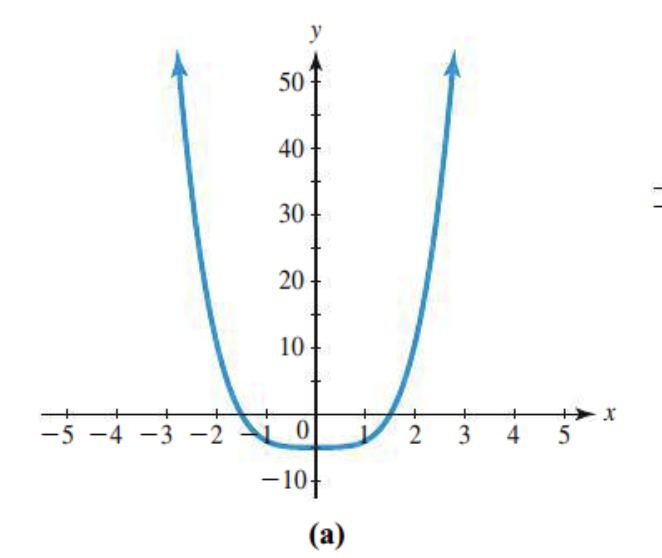
Odd or even degree?

The degree is even as both end behaviors are the same

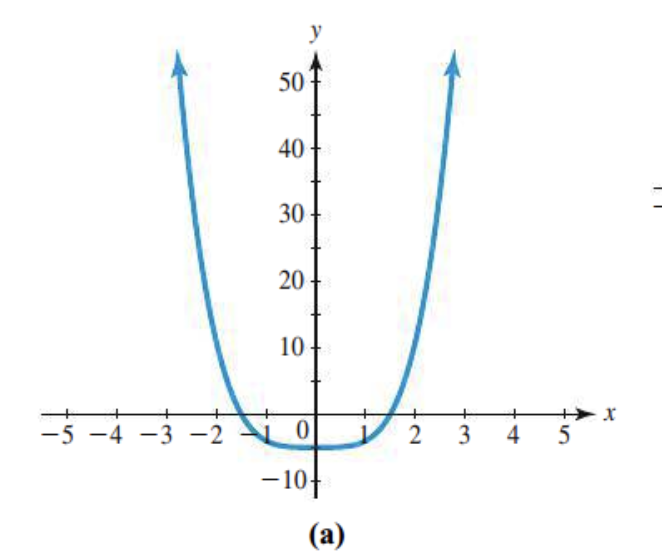
End behavior?

Positive/ same

Number of x-intercepts

One x-intercept

Number of turning points

Didnt change direction: 0

The leading coefficient

It finishes down, its negative

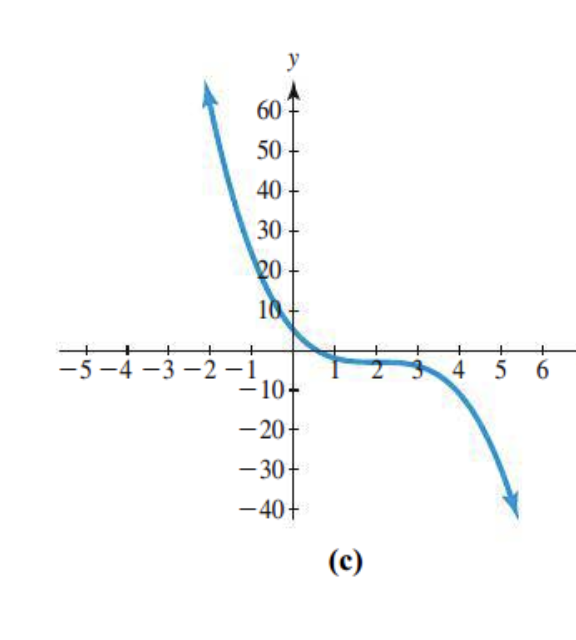
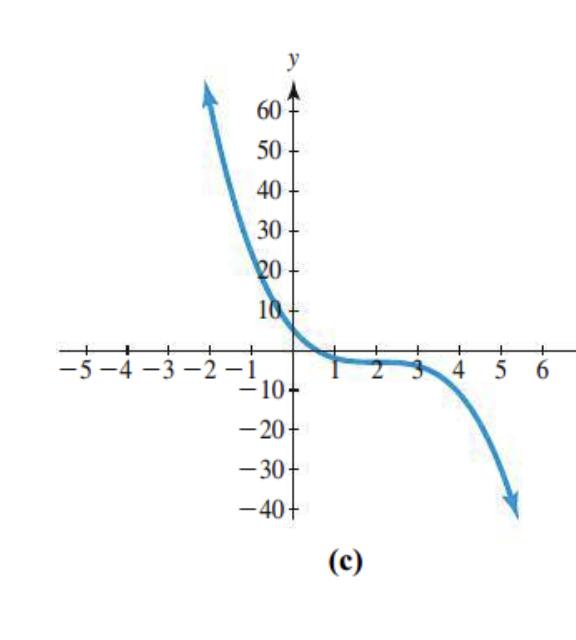
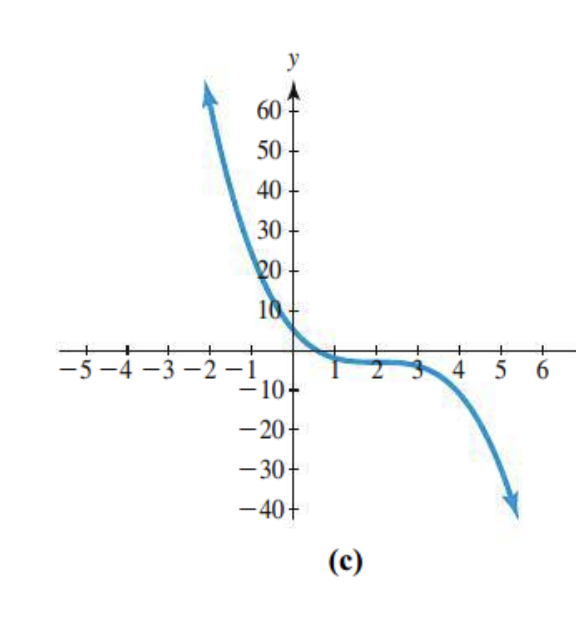
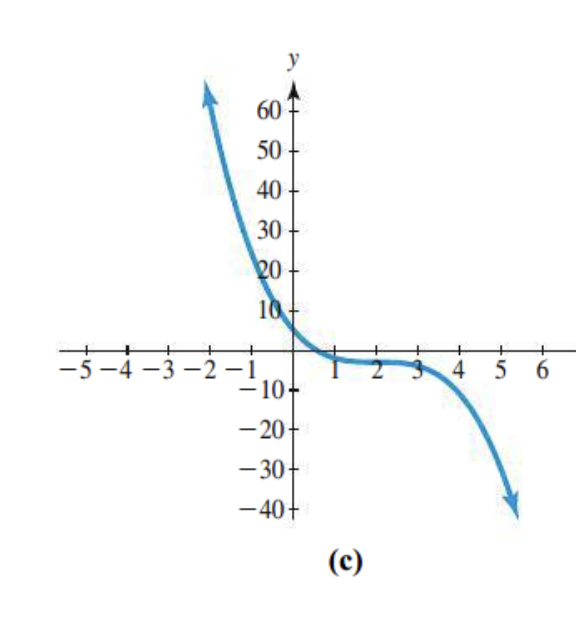
Odd or even degree?

Direction end degrees: odd

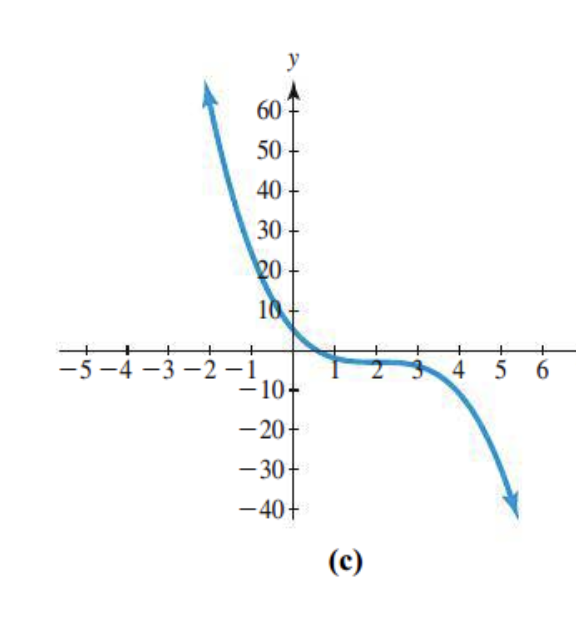
End behavior?

Opposite direction

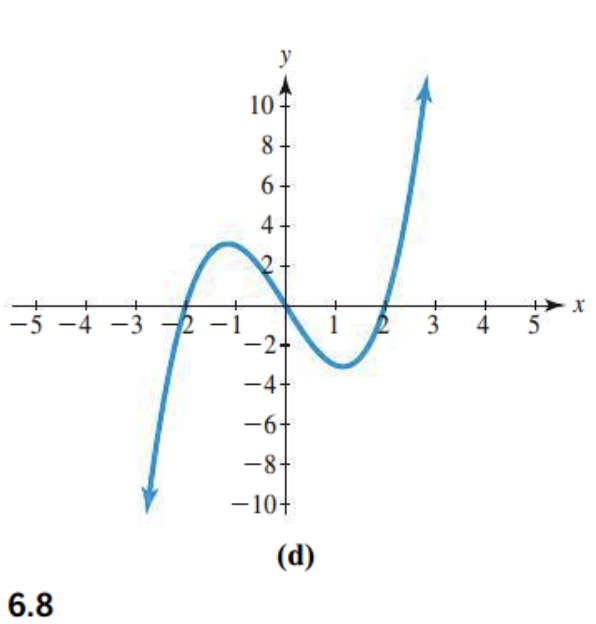
Number of x-intercepts

there are 3 intercepts

Number of turning points

There are 3 turning points

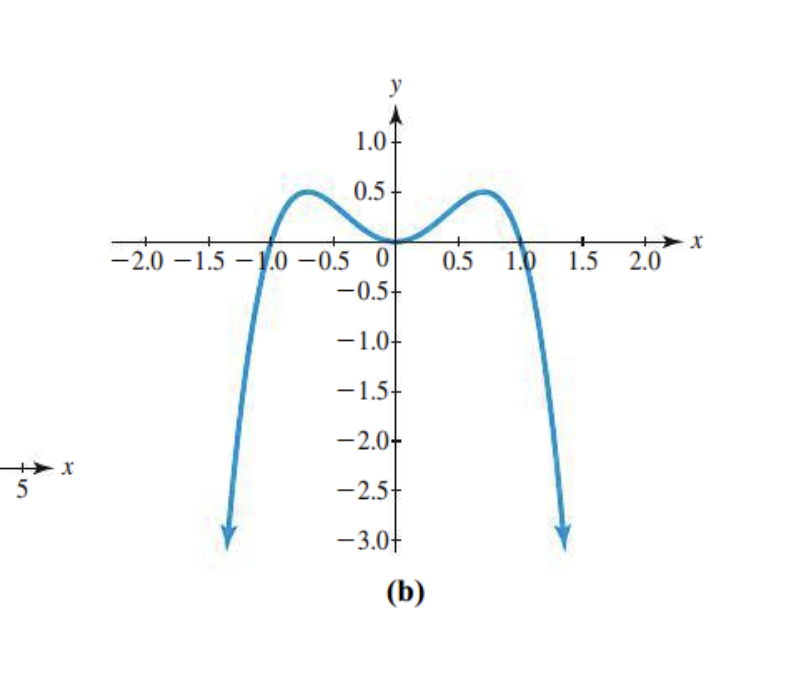
The leading coefficient?

Finishes down: negative

Even or odd degree?

Same direction: even

End behavior?

Same

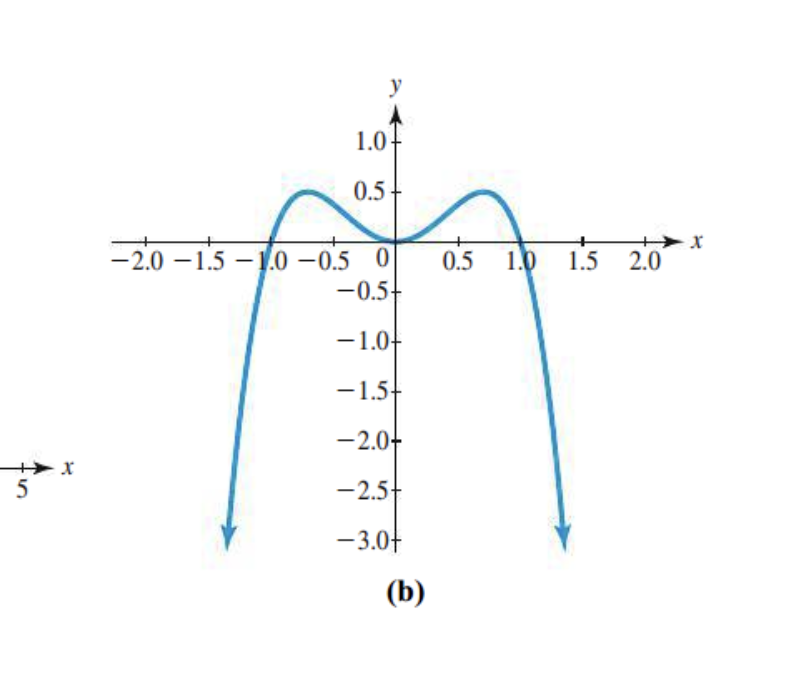
x intercepts?

there are 3 points

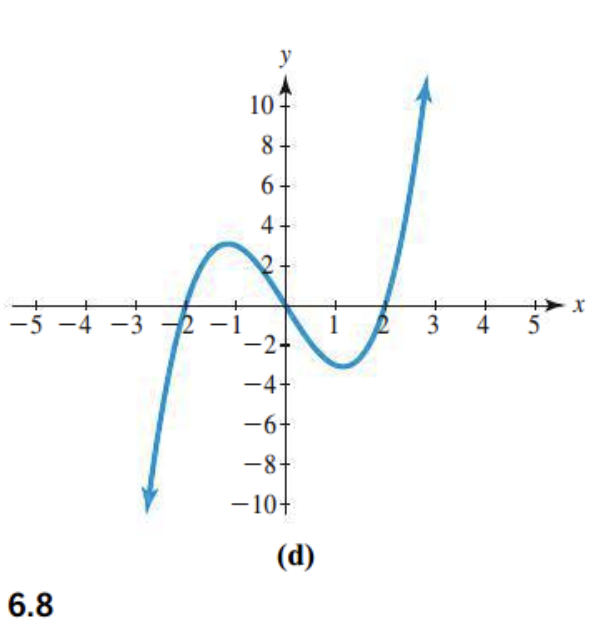
turning points

2 turning points

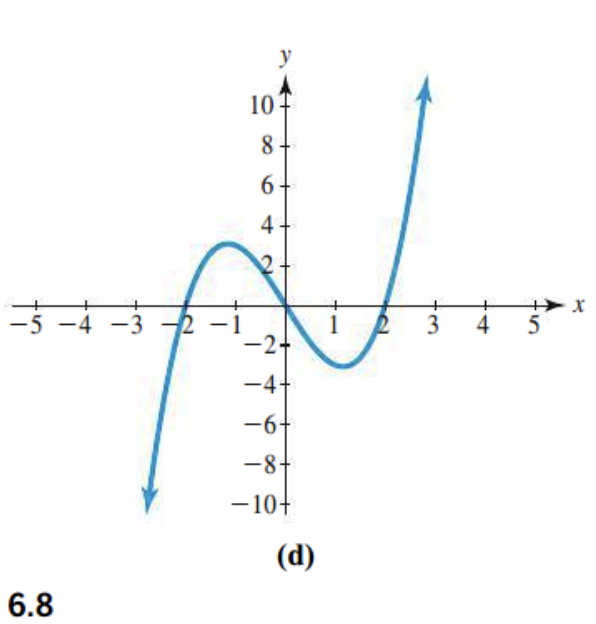
leading coefficient?

finishes up: positive

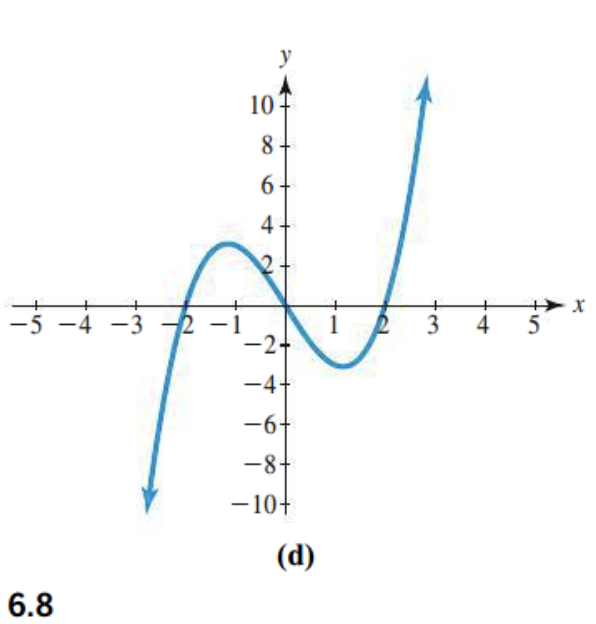
Odd or even degree?

Different end directions: odd

End behavior?

Opposite directions.

If the graph ends in the same direction, what is the degree?

The graph would be even

If the graph ends in opposite directions, what is the degree?

The graph would be odd.

If the graph is an even degree, what is the end behavior

The end behavior would be in the same direction

If the graph is an odd, what is the end behavior

The end behavior would be in opposite directions.

If the graph finishes up, what is the LC?

The leading coefficient is positive.

If the graph finishes down, what is the LC

The leading coefficient is negative.

y=x^4+28x³+292x²+1344x+2304

• how to find local minima?

• graph the equation

• minimum point where turning point is

=x^4+28x³+292x²+1344x+2304

• how to find local maximum?

• graph the equation

• maximum point where turning point is.

Sketch a graph of any cubic polynomial function that has a positive leading coefficient and one​ x-intercep

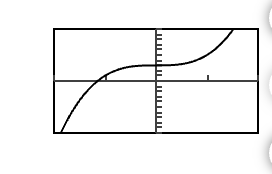
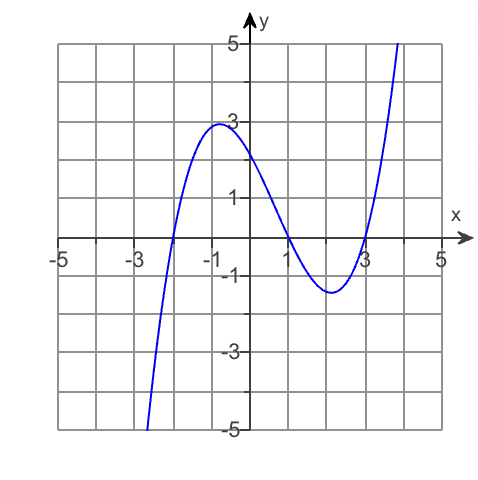
What are the x-intercepts?

-2,1,3

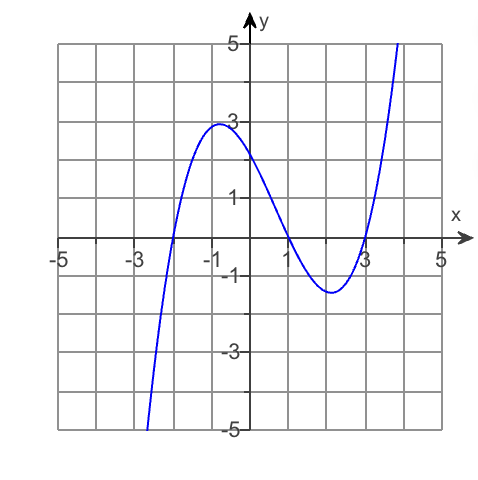
What is the LC

Positive

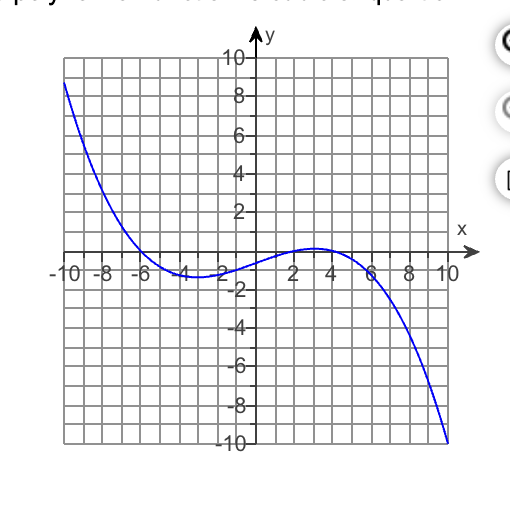
What are the x-intercepts

-6,2,4

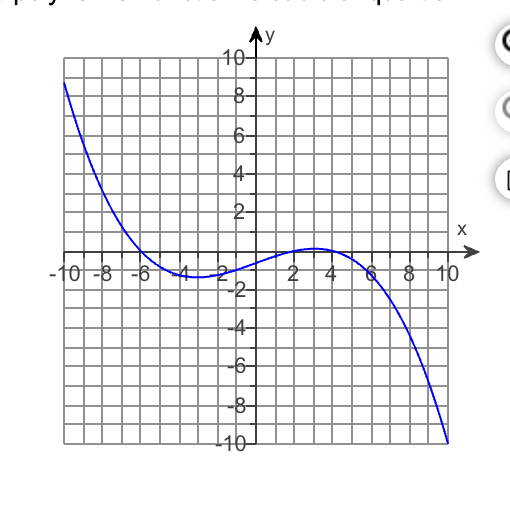
what is the leading coefficient?

Negative

This is the general form of circles

Ax²+Ay²+Bx+Cy+D=0

For circles: This is the formula for finding distance between two points

d = √((x₂ - x₁)² + (y₂ - y₁)²)

For circles: This is the formula of a line segment joining (x1,y1) and (x2,y2), this is also called the midpoint formula, helpful for finding centers when give points from the radiussy

(x1+x2/2), (y1+y2/2)

This is the standard form of a circle

(x - h)² + (y - k)² = r²

(x+1)²+(y-2)²=16,

• Find the center

Opposite signs

• (-1,2)

(x+1)²+(y-2)²=16

• Find the radius

4 (since r² = 16)

The center of a circle is (-1,2) and the radius is 4, how would you graph the circle

You would plot the center point at (-1,2) and use a compass or draw freehand to create a circle with a radius of 4 units around that center. (Up, down, right, and left)

A circle with endpoints of a diameter at (3,-3) and (-6,2): Find the midpoint

Midpoint:

• (3+(-6)/2)= -1.5

• -3+2/2= -0.5

(-1.5,-0.5) and (3,-3): Use the distance formula

d = √((x₂ - x₁)² + (y₂ - y₁)²)

Change answers into fractions

(9/2)²+(-5/2)²= (81/4) + (25/4) = 106/4= 106/2

(x-2)²+(y+3)²=9: Find the center and radius

Center: (2,-3), Radius: 3

Find the domain: 3x²-5/x+2

The domain is all real numbers except where the denominator equals zero, specifically x ≠ -2.

• x+2=0

• -2 on both sides

• x=-2

• (-infinity, -2) U (-2, infinity)

Find the domain: 1/x²-25

The domain is all real numbers except where the denominator equals zero, specifically x ≠ 5 and x ≠ -5.

• x²-25=0

• +25 on both sides

• square root of 25, x=-5, x=5

• (-infinity, -5) U (-5,5) (5, infinity)

Find the domain: x²-4/x-2

The domain is all real numbers except where the denominator equals zero, specifically x ≠ 2.

• x-2=0

• x=2

• (-infinity, 2) U (2, infinity)

Horizontal Asymptote: If your top is larger than your twink

Top destroys twink, no more horizontal asymptote

Horizontal Asymptote: If you top and twink are vers (8x^4-3x/4x^4-7)

The degrees of the numerator and denominator are equal, the horizontal asymptote is found by dividing the leading coefficients, which in this case is : 8/4=2

Horizontal Asymptote: If your TWINK overpowers your top

Horizontal ass would be y=0

graph the equation: x²+y²-6x-10y=2

• Group the bitch

  • x²-6x/ 2=-3²=9 / (x-3)²

  • y²-10y /2=-5²=25/ (x-5)²

• 2+25+9= 36

• (x-3)²+(y-5)²=36

Give me the center and radius: (x-3)²+(y-5)²=36

You flip the h and the k, and square root the equal sign

Center (3,5) radius 6

Write the equation of the circle with center at (-3,4) and radius 5

• Formula: (x-h)²+(y-k)²=r²

You flip the signs and square the radius

• (x+3)²+(y-4)²=25

Write equation in standard form with center at (-8,0) and radius of 8

(x+8)²+y²=64

Write equation of the circle with center (2,-3) and radius 3/2

(x-2)²+(y+3)²=9/4

Final the center and radius of the circle with given equation: (x-10)²+(y+2)²=70

Center: flip the signs (10,-2)

Radius: Square root the answer: Square root of 70