4.2 regular languages

regular languages

sets of strings which can be defined by finite state machines and regular expressions

finite state machines

an abstract mathematical model of computation with a finite set of states and rules defining how it transitions through these states

used to describe simple algorithms

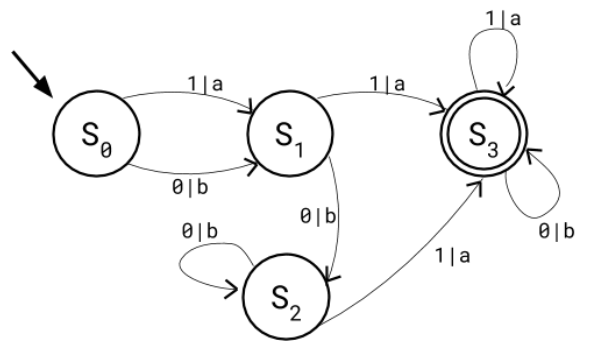
state transition diagrams

diagrams representing FSMs with:

-states as circles labelled Sn

S0 is the start state

a double-outlined circle is the stop state

stop states can be left if an arrow is pointing out

-arrows leading from one state to another (or from a state to itself)

-arrows are labelled with the input that cause the corresponding state change

-inputs may be paired to outputs with | separating them

set

an abstract data type containing unordered unique values (values can be other sets)

notated as S : {item, item, item}

set comprehension

a method of creating a set by specifying rules rather than the individual values

[name] = { [formula in relation to x] | x ∈ [set] ∧ [bounds of x] (optional: ∧ [second bound of x]) }

e.x. S={x*3|x∈ℤ ∧ x≥-3 ∧ x<3}

empty set notation

{} or Ø

compact set representation

highly compact ways of describing sets with simple rules

e.x. {0^n1^n | n > 0}

describes 01, 0011, 000111 etc

finite sets

sets with a finite number of items, the cardinality of a finite set refers to the number of elements within it

infinite sets

sets with an infinite number of items, can be countably or non-countably infinite

countably infinite sets

sets that could theoretically be listed in a logical order given infinite time

non-countable infinite sets

sets that could not be theoretically listed in a logical order given infinite time

countable vs non-countable infinite sets

countable:

natural numbers and integers, as they follow a clear order (even though integers can’t be listed in order of magnitude, they can be listed as 0, 1, -1 etc)

rational numbers, as they can be written as fractions with integers on either side, and can thus be listed in a logical pattern even if they would be impossible to order in terms of magnitude (method of doing this is long to explain and isn’t required knowledge for the exam)

non-countable:

real numbers, as many recur infinitely so could never be listed even given infinite time, and there is no logical pattern in which they could be ordered

subset

a set is a subset of another set if it only contains items present in that set

notated as subset ⊆ set

proper subset

a set is a proper subset of another set if it only contains items present in that set, AND it does not contain all of the items present in that set

countable sets

all finite sets, and all countably infinite sets

membership

an item’s presence in a set

denoted as item ∈ set

lack of membership is denotes as item ∉ set

set operations

operations allowing sets to be constructed from other sets using three operations: union, intersection and difference

union

set1 ∪ set2

creates a set with all values from the sets

intersection

set1 ∩ set2

creates a set with only values present in both of the sets

difference

set1\set2 or set1 - set2

creates a set with values present in set1 but not in set2

regular expressions

shorthand ways of describing sets using metacharacters ( * + ? and | )

*

metacharacter describing 0 or more repetitions of the previous character

e.x. ab* matches to {a, ab, abb … }

+

metacharacter describing 1 or more repetitions of the previous character

e.x. ab+ matches to {ab, abb, abbb … }

?

metacharacter describing 0-1 repetitions of the previous character

e.x. colou?r matches to {colour, color}

|

metacharacter describing an instance of either the character before or after

e.x. a|b matches to {a, b}

()

used to group multiple characters as one in regular expressions

e.x. a(bc)* matches to {a, abc, abcbc … }

a(bc)+ matches to {abc, abcbc, abcbcbc … }

abc(de)? matches to {abc, abcde}

(ab)|(bc) matches to {ab, bc}

expressing regular expressions as finite state machines

-the input string is read by the FSM character-by-character

-when the FSM has halted, the string produced is deemed as valid for the corresponding regular language

-if it cannot halt, the input is deemed as invalid

(ie if it FSM is stuck in a non-halting state which it cannot transition out of, or if a read character does not have a corresponding transition)

* in a FSM

creates a self-transition corresponding to the character before the *

if multiple characters are included before the * in brackets, each character transitions to a new state until the last character which transitions back onto the original state, forming a loop

+ in a FSM

creates a transition corresponding to the character before the + to another state, which has a self-transition for further occurrences of the character

if multiple characters are included before the + in brackets, each character transitions to a new state, then the state for the last character has a transition triggered by the first character, leading back onto the state for the first character

? in a FSM

creates one transition to a new state for the character

if multiple characters are included before the ? in brackets, each character contains a transition to a new state

| in a FSM

creates one transition for each option leading to the same state

if multiple characters are included on either side of the | in brackets, each character on that side contains a transition to a new state until the last character which transitions to the shared state