Oscillations

NB: Do all calculations in Radians for this topic

What is the definition of Simple Harmonic Motion?

An oscillating motion of an object which its acceleration is proportional to its displacement from a fixed point and is directed towards that point

What is equation for simple harmonic motion?

Acceleration= Angular frequency² X Displacement

(a=-ω²x)

(ω² is constant for the object)

What are the key features of simple harmonic motion?

• The acceleration of the object is directly proportional to its displacement, (a is directly proportional to x)

• The minus sign means that the acceleration of the object acts in the direction opposite to the displacement (returns the object to the equilibrium position)

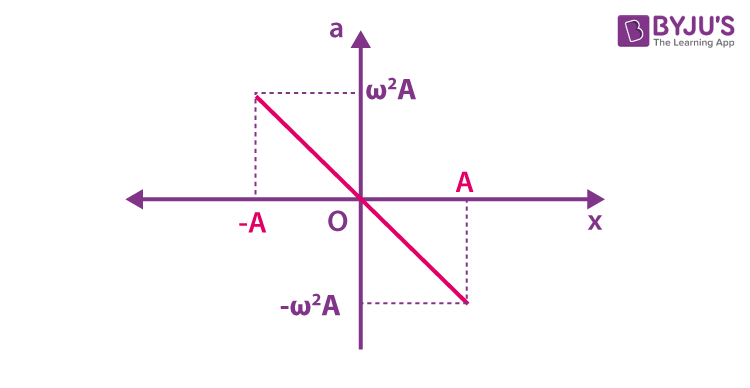
Sketch a graph of acceleration against displacement for any object moving with SHM, and label key features?

• The gradient of the graph is equal to -ω²

• ω= angular frequency of the oscillating object

Explain why the time period, T of an oscillator is independent of the amplitude?

• The period of a simple pendulum moving in SHM does not depend on the amplitude of the swing

• As the amplitude increases so does the average speed of the swing, (so the period does not change, as it must remain constant in SHM)

What does isochronous mean in terms of Simple Harmonic Motion?

An oscillator which has the same time period, and is independent of amplitude

(No matter how big or small the amplitude, it will take the same time period, this means velocity must change to keep it constant)

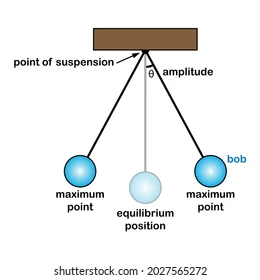
Sketch a diagram of a pendulum oscillating with SHM?

Indicate when the acceleration is greatest and when it is 0

• At the maximum downward displacement (left side) there is maximum acceleration

• At the maximum upward displacement (right side) there is maximum acceleration

• At the equilibrium position (middle) there is 0 acceleration

Sketch a displacement-time graph for an object in SHM?

Define displacement in SHM?

The distance from the equilibrium position

Define amplitude in SHM?

The maximum displacement from the equilibrium position

Define time period in SHM?

The time taken to complete 1 full oscillation

Define frequency in SHM?

The number of complete oscillations per unit time

How is angular frequency calculated?

ω=2π/T or ω=2πf

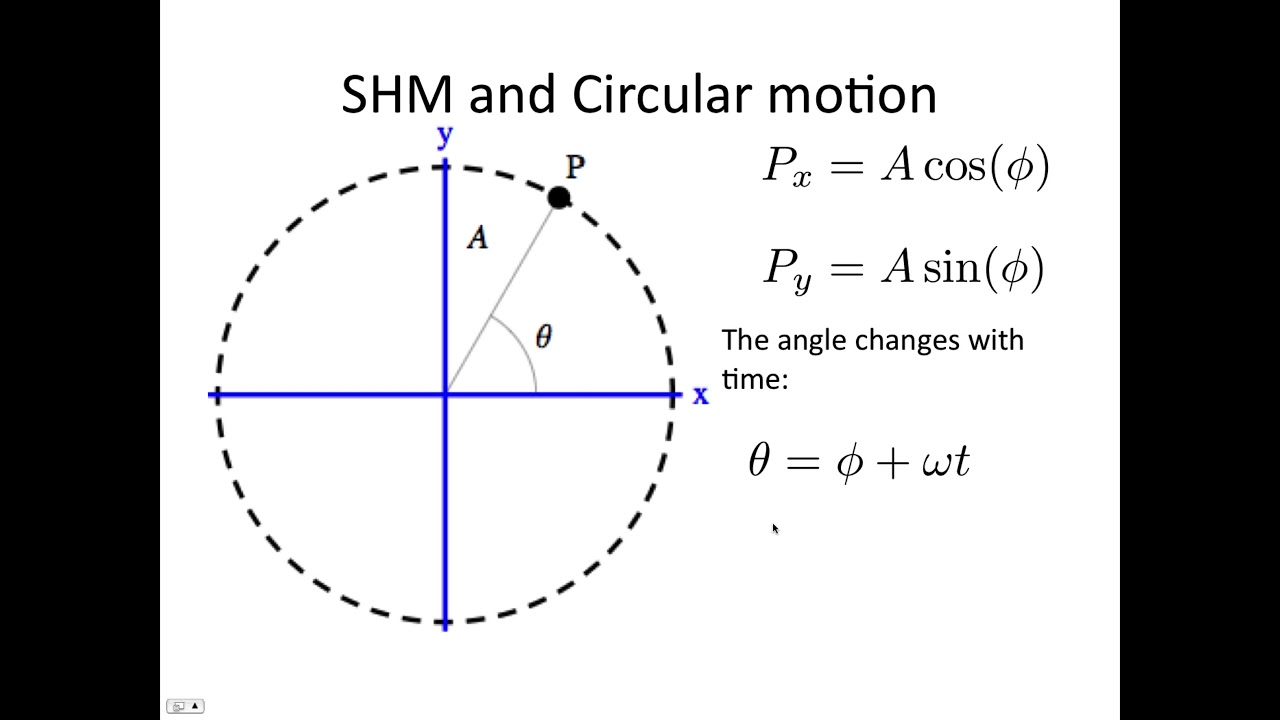
One complete oscillation has similar characteristics to one complete revolution in circular motion

Explain the connection between circular motion and SHM?

Include a diagram

• A Rolling ball travels at a constant angular velocity in a circle of radius, A → The motion of this object along the x-axis can be useful for displacement x=Acosθ (θ = ωt), so you get:

• x=Acos (ωt)

• The angle θ increases uniformly with time, so the graph of displacement, x against time, t is similar to a rolling ball, so it shows SHM

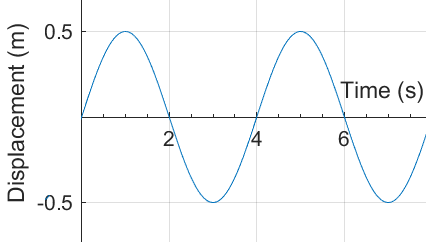
Sketch a:

• displacement-time graph,

• velocity-time graph

• acceleration time graph

for an object moving with SHM

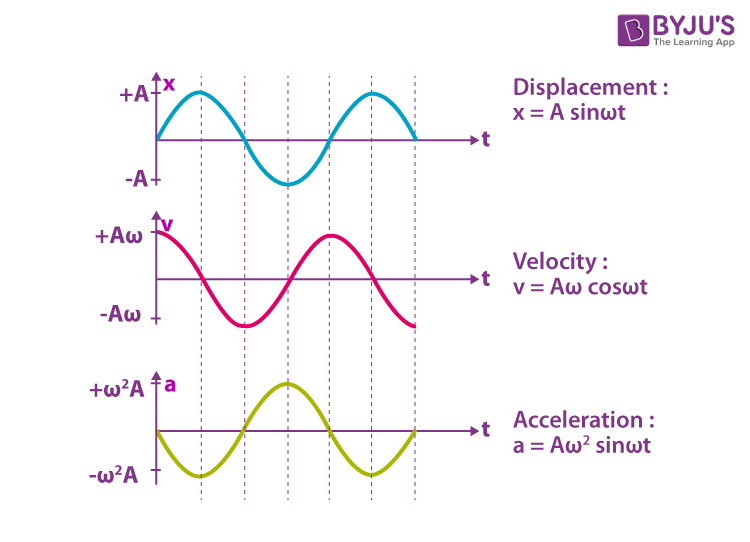
State 2 equations that can be used to describe how the displacement of a simple harmonic oscillator changes with time?

(depending on where the oscillating object is at when t=0, which equation will you use?)

• x= Acosωt, (this equation will be used if an object begins oscillating from its amplitude, then t=0 is at the positive amplitude)

• x=Asinωt. (this equation will be used if an object begins oscillating from its equilibrium position, then t=0 is at the equilibrium position)

What equation can be used to calculate the velocity of a simple harmonic oscillator at displacement, x?

v = ±ω√A²-x²

How can the maximum velocity of a simple harmonic oscillator be determined?

V(max)=ωA

Explain why increasing angular frequency increases maximum velocity?

The oscillator is isochronous (Time period is constant), so it will travel a greater distance in the same time interval, hence the maximum velocity of the oscillator will also increase

Explain why increasing amplitude increases maximum velocity?

The oscillator will be travelling a larger distance at the same time interval, therefore maximum velocity will increase to keep the time period constant

Is frequency and amplitude independent from each other in Simple Harmonic motion?

Yes

For any object moving with SHM, what can be said about the total energy?

Total energy remains constant

Describe the energy changes that take place for a pendulum oscillating with SHM?

• At maximum displacement, there is maximum potential energy and 0 kinetic energy

• At the equilibrium position there is 0 potential energy and maximum kinetic energy

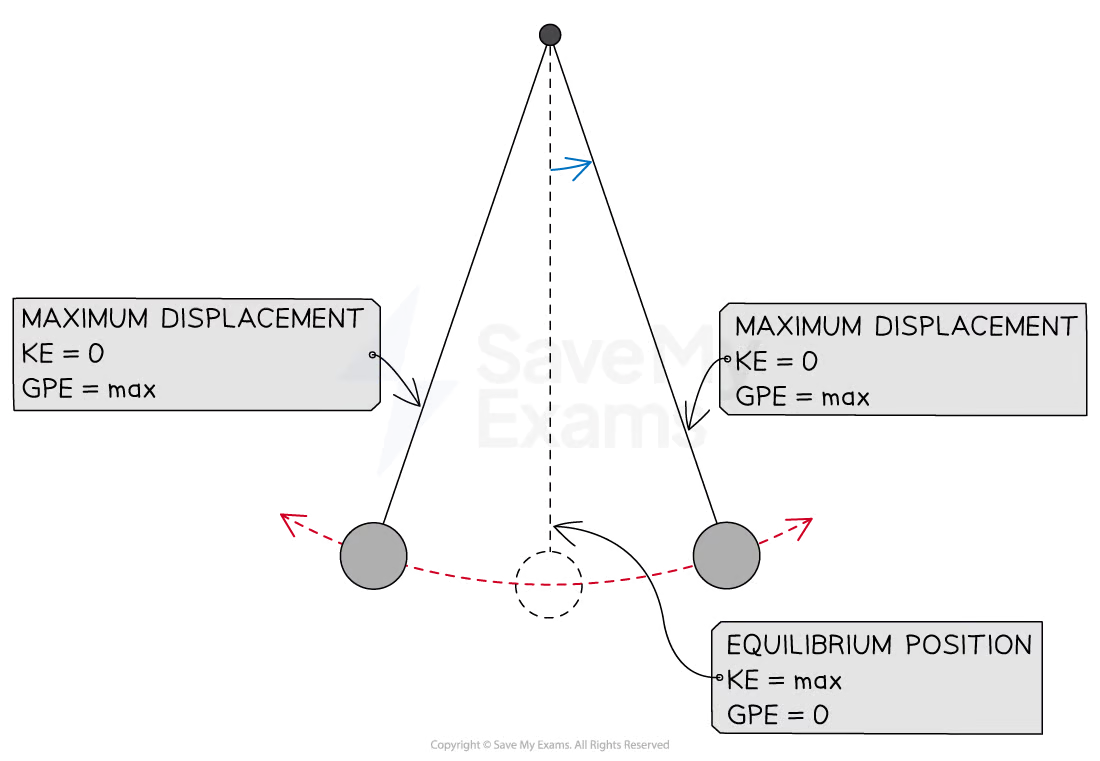
At which position does a pendulum have maximum gravitational potential energy?

When it is at maximum displacement

Describe the energy changes that take place for a vertical spring system oscillating with SHM?

If the mass is oscillating vertically, the potential energy is in the form of gravitational potential energy and elastic potential energy

Describe the energy changes that take place for a horizontal spring system oscillating with SHM?

If the mass is oscillating horizontally, the potential energy is in the form of elastic potential energy only

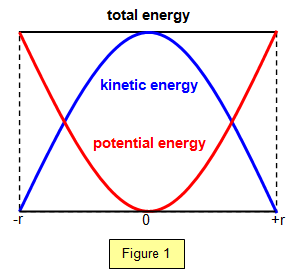
Sketch a graph to show how kinetic energy, potential energy and total energy change with displacement from the equilibrium position?

+r= +A (amplitude)

-r= -A (amplitude)

What is the equation for the elastic potential energy of a spring?

E(p)= ½ Kx²

Elastic potential energy= ½ X force constant X extension²

Write an expression for the maximum elastic potential energy of a horizontal spring system oscillating with SHM, and how is the value related to the total energy of the system?

The elastic potential energy is always positive and varies from E(p)=0, when x=0 to E(p) = ½ k A². when x=A (amplitude)

When x=A, the glider will be stationary for an instant. This means that it has no kinetic energy. Total energy must equal to ½ k A²

Write an expression for the total kinetic energy of a horizontal mass spring system oscillating with SHM?

The E(k) of the glider at any instant must be the difference between total energy and the elastic potential energy therefore, E(k) = ((½ k A² - ½ k x²)) = ½ k (A² - x²)

E(k) = ½ k (A² - x²)

What does it mean if we say an oscillation is damped?

When an external force that acts on the oscillator has the effect of reducing the amplitude of its oscillations

Give an example of a damped oscillation?

A pendulum moving through air experiences air resistance, which damps the oscillations until eventually the pendulum comes to rest

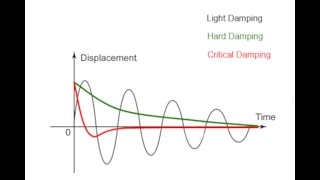
Describe light damping?

When the damping forces are small, the amplitude of the oscillator gradually decreases with time, but the period of the oscillations is almost unchanged

Describe heavy damping?

The amplitude decreases significantly, and the period of the oscillations also increases slightly

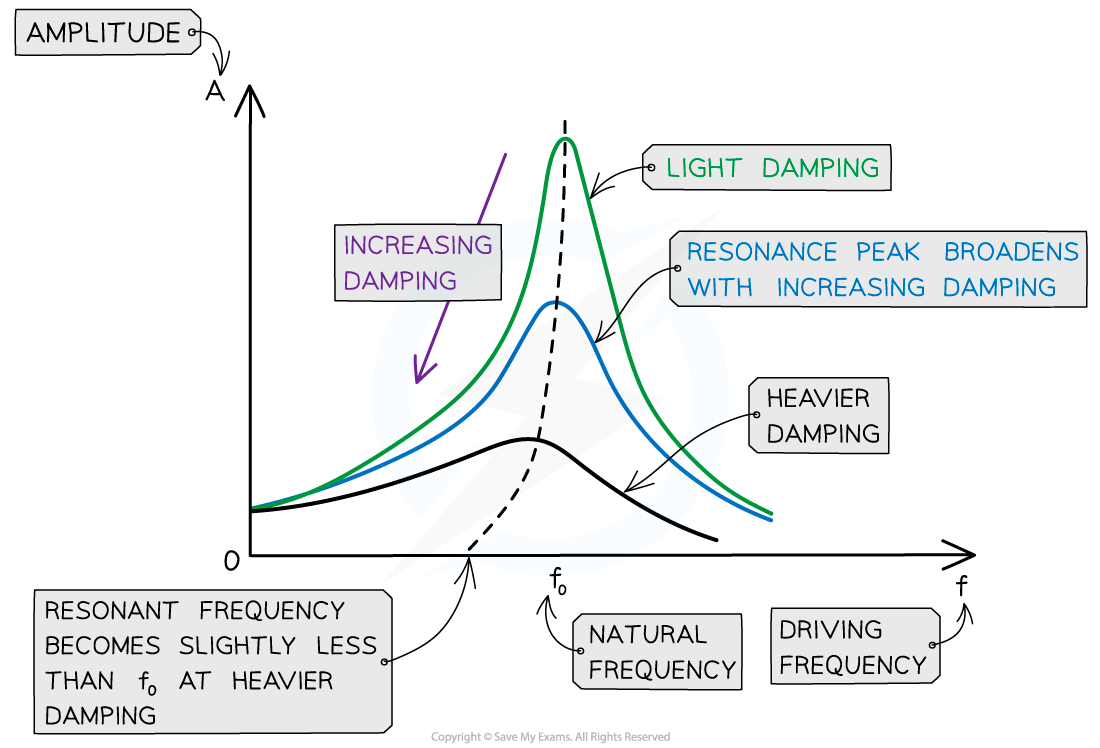
Sketch a displacement-time graph for an oscillator with:

• light damping (blue)

• heavy damping (red)

• very heavy damping (green)

What happens to the kinetic energy of the oscillator when it is damped?

It gets transferred to other forms, usually heat

Define the term “free oscillation”?

When a mechanical system is displaced from its equilibrium position and then allowed to oscillate without any external forces

Define “natural frequency”?

The frequency of the free oscillations

Define the term “forced oscillation”?

Where a periodic driver force is applied to an oscillator, the object will vibrate at the frequency of the driving force

What happens when the driving frequency of an oscillator is equal to the natural frequency of the oscillator?

The object will resonate- causes the amplitude of the oscillations to increase drastically (if not damped, the system may break)

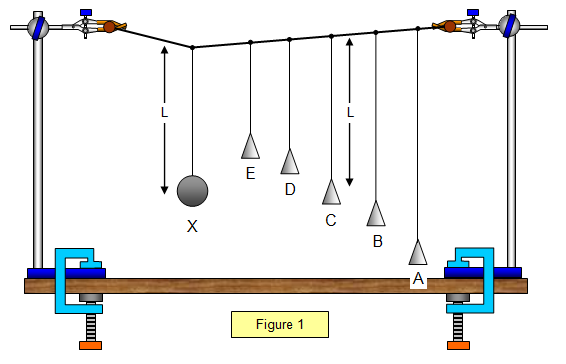
Explain how Barton’s pendulums demonstrate resonance?

• A number of paper cone pendulums of varying lengths are suspended from a string along with a heavy brass bob, X

  • This heavy pendulum, X oscillates at its natural frequency and forces all the other pendulums to oscillate at the same frequency

• As pendulum C has the same length as pendulum X it has the same natural frequency- it will resonate and its amplitude will be greater than the other pendulums

What is resonance?

It occurs when the driving frequency of a forced oscillation is equal to the natural frequency of the oscillating object

If there is no damping, what condition must be met for resonance to occur?

Frequency of the periodic driving force must be equal to natural frequency of the free oscillations

→The amplitude will increase to the point which the object falls

Give 2 examples of resonance?

• EM microwaves oscillates at the natural frequency of the water molecules in food causing a great energy transfer in order to warm food

• Someone’s voice can match the natural frequency of a glass and then sing that pitch as the sound waves oscillate the glass and then break the glass

Why is the amplitude of the forced oscillator greatest at the resonant frequency?

The greatest possible transfer of energy from the driver to the forced oscillator occurs at the resonant frequency

Describe the basic principle of magnetic resonance imaging (MRI)?

• A strong magnetic field created by superconducting electromagnets, the precessions occurs at different natural frequencies.

• Radio waves from transmitting coils inside the scanner cause the nuclei to resonate and absorb energy, when the radio waves are off, the nuclei relax and re-emit the energy gained, producing a 3D image

What is an advantage of an MRI over a CAT scan?

MRIs produces more clearer images of tissues and organs compared to CAT scans

What is the result of damping a forced oscillation?

Reducing the maximum amplitude at resonance (degree of damping also has an effect on the frequency of the driver when maximum amplitude occurs)

Sketch a graph of driving frequency against amplitude of forces oscillation to show how the degree of damping impacts amplitude of oscillations and frequency of which oscillation has maximum amplitude?