Biot-Savart Law

Magnetic Field Produced by Current

A moving electric charge (current) produces a magnetic field that interacts with other currents and magnetic materials.

Biot–Savart Law

An empirical law that gives the magnetic field produced at a point by a current-carrying conductor, accounting for both magnitude and direction.

Differential Form of the Biot–Savart Law

It gives the infinitesimal magnetic field contribution from a small current element.

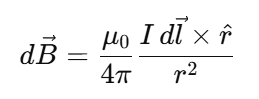
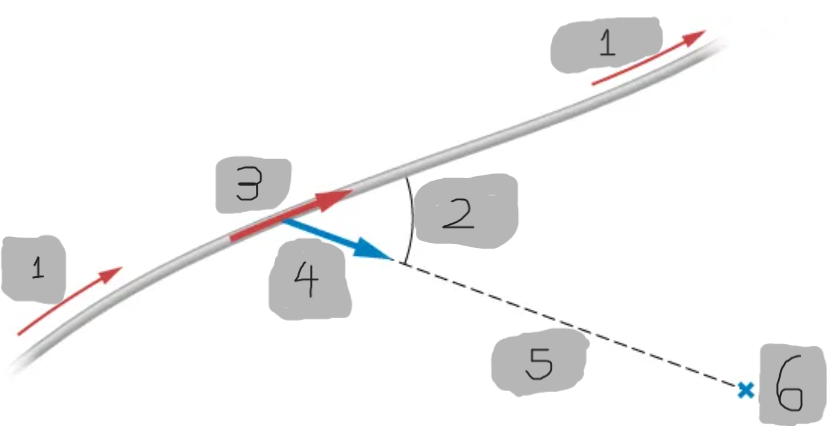
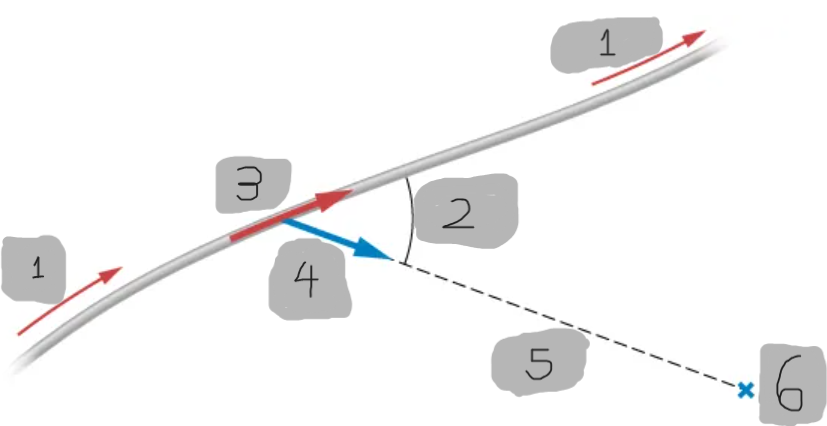
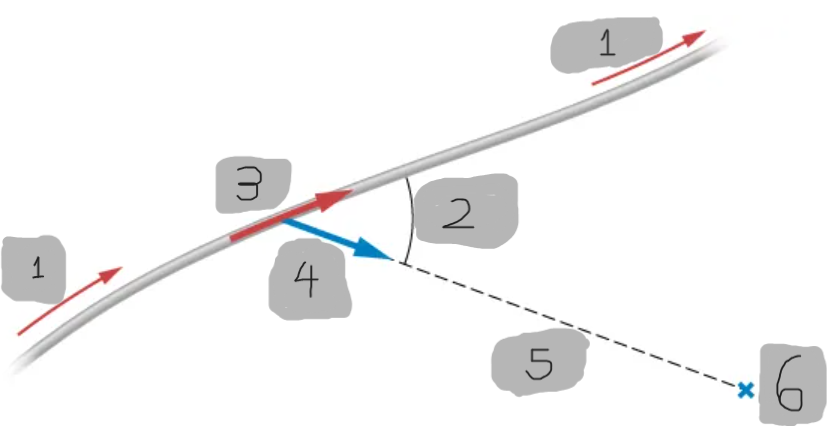
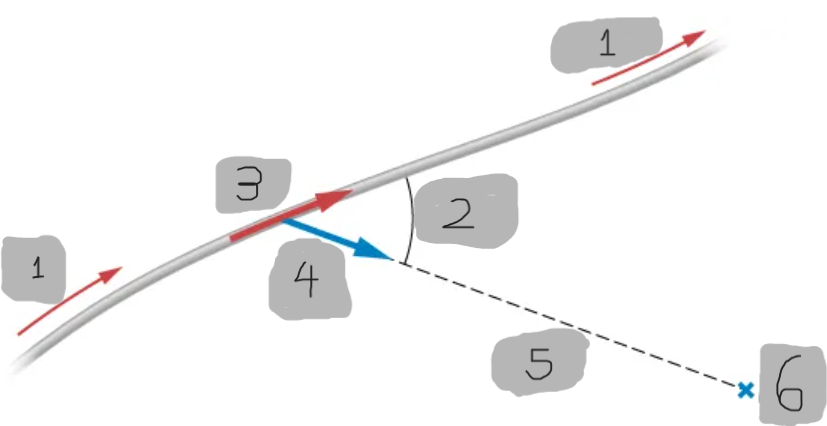
Current Element (dl)

An infinitesimal vector segment of a wire that points in the direction of the current flow.

Unit Vector

A unit vector that points from the current element dl⃗ to the observation point P

Distance r (Biot–Savart Law)

The straight-line distance from the current element dl⃗ to the point where the magnetic field is being calculated.

Permeability of Free Space (μ0)

A physical constant that relates magnetic field to electric current in free space

μ0 = 4π × 10^-7 T⋅m/A

Value of μ0

Direction of dB

Determined by the right-hand rule applied to the cross product dl × r^.

Magnitude of the Differential Magnetic Field

where θ\thetaθ is the angle between dl⃗ and r^

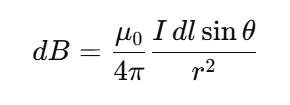
Angle θ (Biot–Savart Law)

The angle between the current element dl⃗ and the unit vector r^

Condition for Zero Magnetic Field Contribution

If θ = 0, then dB⃗ = 0, meaning a current element produces no magnetic field along its own direction.

Integral Form of the Biot–Savart Law

Used to calculate the total magnetic field from a finite current distribution.

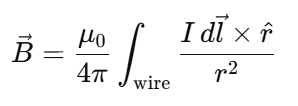
l

(1)

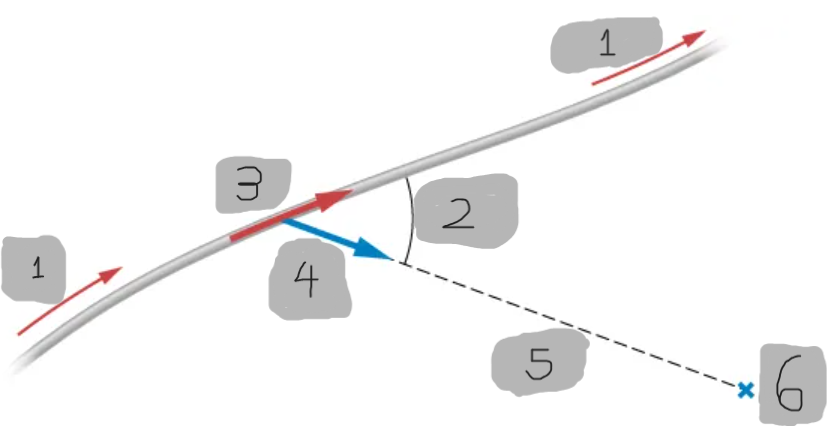
θ

(2)

dl

(3)

ȓ

(4)

r

(5)

dB

(6)

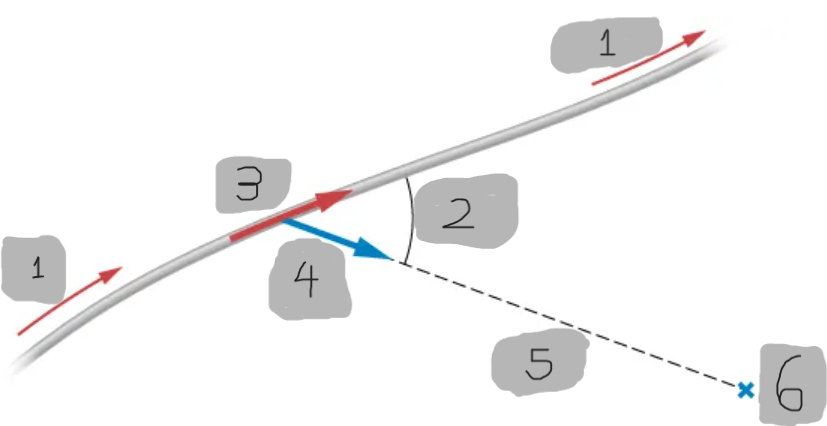
Vector Nature of the Biot–Savart Integral

Contributions from different current elements may point in different directions, making the integral difficult to evaluate without symmetry.

Ampère’s law is preferred over the Biot–Savart law when there is high symmetry between the magnetic field and the current distribution.

When to Prefer Ampère’s Law?

Right-Hand Rule (Biot–Savart)

Curl the fingers of the right hand from dl toward ȓ; the thumb points in the direction of dB

Short Current Segment Approximation

When the current element length is much smaller than the distance to the field point, the Biot–Savart integral can be approximated as a sum.

Magnetic Field of a Short Straight Wire Segment

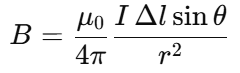
Validity of Short-Segment Approximation

The approximation is valid only when the wire segment length is much smaller than the distance to the observation point.

Direction of Magnetic Field for a Straight Vertical Wire

Determined using the right-hand rule; for upward current, the magnetic field circulates into or out of the page depending on position.

Magnetic Field of a Circular Arc of Wire

The magnetic field at the center of a circular arc carrying current is found using the Biot–Savart law and symmetry.

dl = r dθ

Arc Length Differential that gets used when integrating over a circular arc.

Simplification for Circular Arc Integration

Since dl⃗ and r^ are perpendicular, the cross product becomes simple multiplication.

Magnetic Field at Center of Circular Arc

B = ((μ0×I)/(4πr))θ; where θ is in radians

Direction of Magnetic Field for a Circular Arc

All current elements contribute magnetic fields in the same direction, determined by the right-hand rule.

Superposition Principle (Magnetic Fields)

The net magnetic field is the vector sum of the magnetic fields produced by each individual current or wire segment.

Magnetic Field Cancellation by Symmetry

In symmetric configurations, contributions from opposite sides of a point may cancel each other.