Unit 3- Ratios and Rates; Unit 4- Percentages

Ratio: def-

ex. For every 4 apple there are 3 oranges can be written as

-comparison of 2 quantities

4 apples: 3 oranges —> 4:3

4 for every 3

4 to 3

Equivalent Ratios:

two or more ratios that are equal when simplified

ex. 3:9 —> 1:3

-find ratios, factors, multiples

-consider simplifying down to 1

ex. 5 bags tea: 3ml H₂O —> 1 bag tea: 3/5 ml H₂O

Ratio: def-

ex. For every 4 apple there are 3 oranges can be written as

-comparison of 2 quantities

4 apples: 3 oranges —> 4:3

4 for every 3

4 to 3

Equivalent Ratios:

two or more ratios that are equal when simplified

ex. 3:9 —> 1:3

-find ratios, factors, multiples

-consider simplifying down to 1

ex. 5 bags tea: 3ml H₂O —> 1 bag tea: 3/5 ml H₂O

Part-Part ratios:

Part-Whole ratios:

-compares two parts within a whole; shows how one part relates to another part

-a ratio that compares a selected number of parts to the total number of parts in a whole.

ex. 5 red flowers: 10 yellow flowers —> (15 flowers in this ratio)

-How many red flowers if 45 TOTAL flower?

45/15= 3 —> 3×5 red flowers= 15 red flowers

Unit Rates:

-the ratio of two different units, with denominator as 1

-compares a certain number of units of one quantity to units of another quantity. In other words, the second quantity in the comparison is always 1. 

ex. Box travels 40miles in 2 hours —> 20miles/ 1 hour

-160 words/4 minutes —> 40 words/ minute

A "unit rate" refers to a rate where the denominator is always 1, meaning it expresses a quantity per single unit of another quantity; while "dimensional analysis" is a method of converting units by multiplying a given quantity by conversion factors, strategically arranged to cancel out the original units and leave you with the desired units

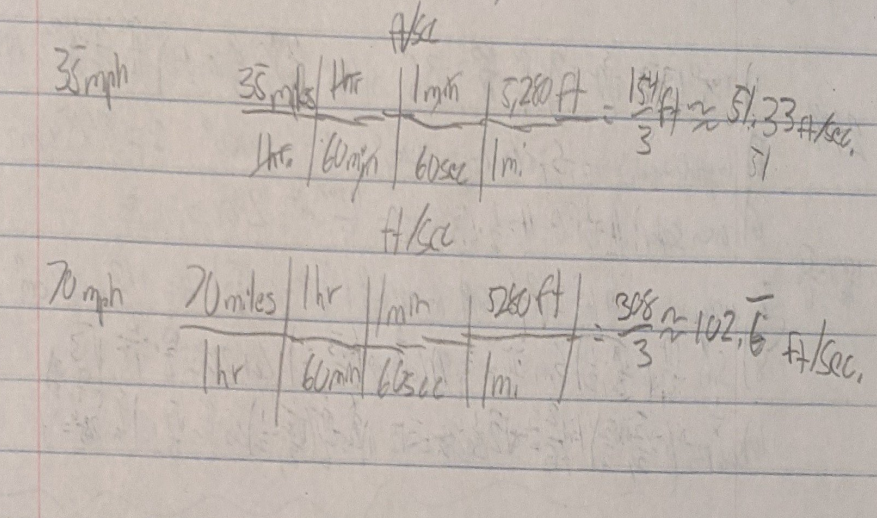
Dimensional analysis:

ex. Convert 35mph to ft/sec

-Convert 70mph to ft/sec

-relates similar measurements to different units through a conversion factor

1)Start with given quantity to the Left

2) Use the conversion factor—> write as Want/ Have

ex. Inches in 37 cm, 1in-2.54cm —> (37cm-given)* (want INCHES/have 2.54cm) conversion factor

ex. 37cm*( 1in/2.54cm)

3) Unit on bottom gets cancelled

*die in the basement

*can also cancel out units on diagonal as seen in mph to ft/sec questions —> just like reducing when multiplying fractions

*tip consider fully converting one unit (ex. hours down to sec) before moving onto the next —> one at a time

ex. CMs cross out —> 37 (inch left over) /2.54= 14.6inches

Percentages: find by dividing

-divide the part by the whole

ex. 9/10 —> 0.9 —> 90%

Convert decimal to % by moving decimal two spots over to the right;

ex. >1.0= >100%, 1.21 —> 121%

Percentage of a whole number:

Fraction Method:

-(Percentage number/ 100)* OF number

ex. 20% of 40 —> (20/100) 40 —>1/5 (40)= 8

Percentage Method:

-make percentage a DECIMAL and multiply OF number

ex. 20% of 40 —> 0.2×40= 8

2 types: of % questions on SAT:

Question 8 is an example of which type?

Question 17?

1) find % of something

vs.

2) finding % LESS/MORE of something

ex. 20% less/more is ACTUALLY asking for 80%

8: 540= 80% OF x —> 540= 0.8x

17: 20% less —> Actually asking for 80% of 40

ex. 8/10 —> 4/5 —> (4/5)*40= 32

-see a %= probably a % question