Congruence with Tranformations- Unit 3

Geometry

Transformation

A change in the size, position, orientation of a figure.

Rigid Transformations

Transformations that preserves congruence

Translation

A transformation which moves each point of a figure the same distance and in the same direction.

Reflection

A transformation which flips the figure over a line

Line of Reflection

The line where the figure is fliped

Rotation

Turning a figure about a fixed point

The 2 D’s of rotations

1) Direction (CW or CCW)

2) Degree ( 90, 180, 270, 360)

Pre image

Figure before the transformations

Image

The resulting figure after a transformation of the pre-image

Final Image

The last transformation given to a figure

General Rule/ Coordinate Notation

The translation rule could be written as (x,y) → (x+_, y+_)

X-coordinate, to the add you go to the

Right

X coordinate, to subtract you go to the

Left

Y coordinate, to add you go

Up

Y coordinate, to subtract you go

Down

Congruent (≅)

Same/equal shape and size

Similar (=)

Same/equal shape but different size

Counterclockwise

Rotating to the right

Clockwise

Rotating to the left

General Rule for a Reflection over line y=x

(x,y) —> (y,x) (Just flip axis)

General Rule for a Reflection over line y=-x

(x,y) —> (-y, -x) (flip axis and signs)

Horizontal lines of reflection- y=#

Whatever number (point) that’s behind the y, replace the y axis going horizontally from that number (point)

Vertical lines of reflection - x=#

Whatever number (point) that’s behind the x, replace the x axis going vertically from that number (point)

90° counterclockwise rotation about the origin is the same as

270° clockwise

The general rule for 90° CCW and 270° CW

(x,y) —> (-y,x)

180° counterclockwise rotation about the origin is the same as

180° clockwise (stays the same)

The general rule for 180° CCW and CW is

(x,y) —> (-x,-y)

270° counterclockwise rotation about the origin is the same as

90° clockwise

The general rule for 270°CCW and 90°CW is

(x,y) —> (y,-x)

360° counterclockwise rotation about the origin is the same as

360° clockwise (stays the same)

The general rule for 360°CCW and CW is

(x,y) —> (x,y) (stays the same)

Two things that need to in order to know if 2 triangles are congruent

1) Congruent sides

2) Congruent angles

Slash markings on a triangle are for

Sides

Arc markings on a triangle are for

Angles

Corresponding Parts

Angles in which are congruent to each other Ex: ∠ A ≅ ∠D

Triangle Congruence Theorems

The five triangle congruence theorems suggest congruence in relation to the triangles, if the none of these methods work on the triangles then they are not congruent

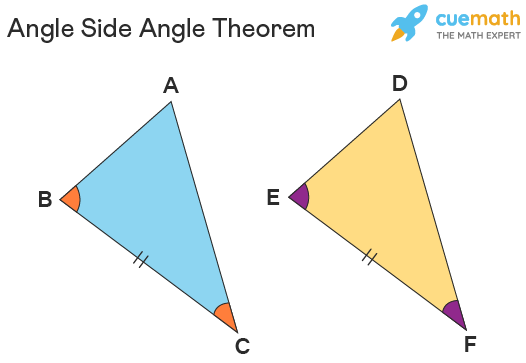
Angle-Side-Angle (ASA)

When two angles and the included side of 1 triangle is congruent to 2 angles and included side of another triangle

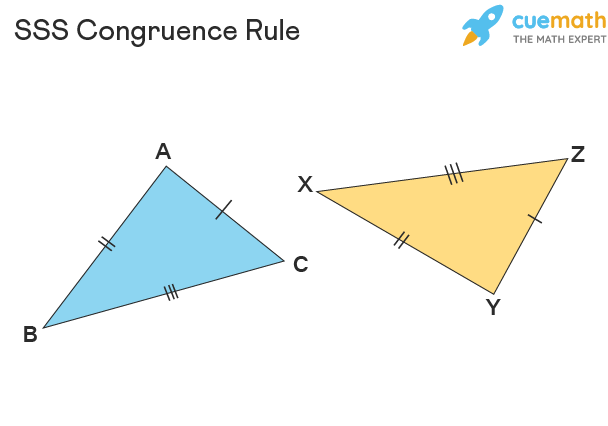
Side-Side-Side (SSS)

When 3 sides of 1 triangle are congruent to 3 sides of another triangle

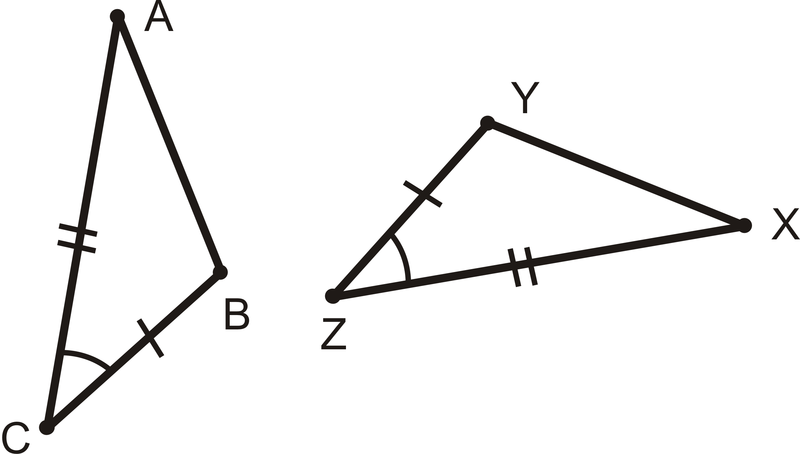
Side-Angle-Side (SAS)

When 2 sides and the included angle of 1 triangle are congruent to 2 sides and included angle of another triangle

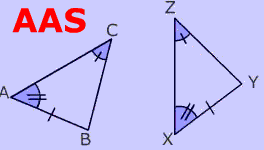
Angle-Angle-Side (AAS)

When 2 angles and 1 non-included side of 1 triangle are congruent to 2 angles and 1 non-included side of another triangle

Hypotenuse Leg (HL)

Hypotenuse and leg of 1 right triangle are congruent to hypotenuse and leg of another right triangle. (Only triangles who have right angles can use this method but make sure it passes through the other methods first.) HAVE TO MAKE SURE IT STATES THAT THE HYPOTENUSE IS CONGRUENT TO EACH OTHER

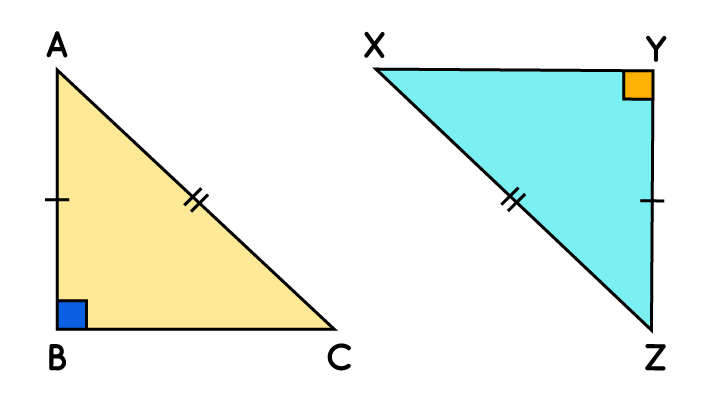
When identifying methods, you have to make sure that

Either angles and sides are next to each other in order

Line Symmetry

When a figure has this it can be reflected onto itself along a line called the line symmetry.

Lines of symmetry

Lines that state ways to split a figure in equal parts

Rotational Symmetry

If the figure can be mapped onto itself by a rotation between 0° and 360° around the center of the figure. (the figure has this when it still lokes the same after a rotation

Magnitude of symmetry

The smallest angle through which the figure can rotate so that it maps onto itself. (for most of the time, divide 360 by the number of lines of symmetry of the figure to get the magnitude)

Triangle Proofs

Are by completing two column proofs which consist by statements and reasons to reach a final proven conclusion

Reflexive Property: AB=BA

When the triangles have an angle or side in common

Vertical Angles are Congruent

When two lines are intersecting

Right Angles are Congruent

When you are given right triangles and/or a square/rectangle

Alternative Interior Angles of Parallel Lines are Congruent

When the givens inform you that two lines are parallel

Definition of a Segment Bisector

Results in 2 segments being congruent

Definition of a Midpoint

Results in two segments being congruent

Definition of an Angle Bisector

Results in two angles being congruent

Definition of a Perpendicular Bisector

Results in 2 congruent segments and right angles

3rd Angle Theorem

if 2 angles of a triangle are congruent to 2 angles of another triangle, then the 3rd angles are congruent

Definition of a Segment Bisector

Results in 2 segments being congruent

NOTE:

Do NOT assume anything if it is not in the given

CPCTC

An acronym for Corresponding Parts of Congruent Triangles are Congruent. Once 2 triangles are proven to be congruent, then the 3 pairs of sides and angles that correspond must be congruent. Is usually at the end of a proof to show that 2 angles or 2 sides are congruent. (ONLY STATE THIS AFTER THE TRIANGLES HAVE BEEN PROVEN TO BE CONGRUENT)