W6 Social Insurance/Adverse Selection

Social Insurance: Motivation

What is social insurance?

Government intervention in markets to insure against adverse events (e.g., health, disability, unemployment), with transfers based on event occurrence, not income.

How does social insurance differ from welfare?

Social insurance is based on events (e.g., becoming unemployed); welfare is means-tested (based on income/assets).

What is expected utility (EU)?

A weighted sum of utility in each possible future state, weighted by the probability of each state.

E.g:

EU = (1−p)∗U(c if no adverse event)+p∗U(c if adverse event)

What does it mean for an individual to be fully insured?

They have equal consumption in all states of the world, smoothing risk perfectly.

What is the insurance problem?

• Individuals face uncertainty about future outcomes — for example, a health issue or accident may or may not happen.

• These outcomes lead to different levels of well-being (utility), depending on consumption in each possible state.

• Insurance allows individuals to transfer resources from good states (where they’re better off) to bad states (where they’re worse off).

In the basic insurance model, what is the income of each state of the world and which income is larger?

E₁ = good state income

E₂ = bad state income

E₂ < E₁

What is the expected utility of an individual under insurance?

Expected utility EU = (1 − p) × U(E₁ − α₁) + p × U(E₂ + α₂)

α₁: net premium paid to insurer in good state (cost)

α₂: net benefit received from insurer in bad state (benefit)

Where α=(α₁,α₂) is the insurance contracts

What is the expected profits of insurers in the basic insurance model?

EP = (1 − p) × α1 − p × α2

If bad state happens (p) then they lose α₂, otherwise they gain pay out of α₁

What is the expected profits of insurers under perfect competition? What does the result give us?

Under perfect competition, insurers cannot make a profit in the long run (due to free entry) so EP = 0

EP = (1 − p) × α₁ − p × α₂ = 0

α₂= 1-p/p * α₁

A contract that satisfies this condition is called actuarially fair

What is an actuarially fair contract?

A contract where the insurer’s expected revenue equals its expected payouts

(1 − p) × α₁ = p × α₂

OR more commonly α₂= 1-p/p * α₁

How do we find out how much insurance individuals demand and pay under an actuarially fair contract?

1. Maximise individual expected utility with respect to α₁ having subbed in the actuarially fair contract (α₂= 1-p/p * α₁) so whole EU in terms of α₁

2. FOC gives U’(E₁ - α₁) = U’(E₂ + α₂)

3. Since we have U’>0 and U’’<0 (concave utility) we can say E₁ - α₁ = E₂ + α₂

4. We know this is the consumption in good state and consumption in bad state so c₁ = c₂

5. Result: they demand full insurance as consumption equal in both states

6. To get how much they pay: do c = (1-p)*E₁ + p*E₂ and use that c = E₁ - α₁

7. Result: individuals pay: α₁ = p *(E₁ - E₂)

What is the fundamental result of basic insurance theory?

At an actuarially fair price, risk averse individuals will always demand full insurance (to smooth consumption across states)

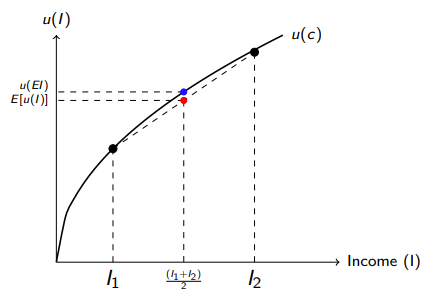
What is this graph showing?

u(EI) = U(expected income) = utility when insurance fair

E[u(I)] = Expected utility = utility when no insurance

Risk averse individuals (with concave utility): U(expected income)>Expected utility

In other words, they'd rather have certain average income than uncertain income with the same expected value.

Risk averse individuals would still be better off buying full insurance at less than actuarially fair price (up to a point!)

If insurance not fair and insurers are making a profit then I is less than I₁+I₂/2 so slightly eats into your income but you are still better off until I₁

How would asymmetric information affect the model in general?

If symmetric: both insurers and individuals observe the risk type pi (e.g. through observing age, health history, driving record etc)

If asymmetric: only individual knows their own risk

What do insurers do if there is symmetric information? Do they sell actuarially fair contracts?

Insurers will sell different policies for each type pi

With perfect competition, each policy will be actuarially fair

Each type will buy full insurance and consume c1 = c2 = (1 − pi) × E1 + pi × E2

Is the private insurance market efficient when there is symmetric information?

Yes, each policy will be actuarially fair and according to the fundamental result of basic insurance theory, risk averse individuals will always demand full insurance at this price

If everyone gets full insurance then there are equalised incomes within types across states of the world aka everyone with probability p gets same income

What is adverse selection? When does it occur?

Adverse selection is a market failure that occurs when one side of the market has private information that the other side doesn’t have

It occurs when there is asymmetric information in the market

In context of insurance: People who know they are high risk (more likely to claim insurance) are more likely to buy insurance, while low-risk people opt out — especially if everyone is charged the same price.

What is the setup for the model of adverse selection in the insurance market? When is the socially efficient outcome?

Many individuals (a continuum) in a population G(ξ), each with their own characteristics ξi​, e.g., risk level.

Only 1 possible contract: Full-insurance contract H or no insurance L

Due to asymmetric information, there is only one price p for all

Individual buys insurance if π(ξi) ≥ p so if their willingness to pay is at least the price

Assume perfect competition => p = AC(p) and AC(p) = E[c(ξi)|π(ξi) ≥ p] aka average cost of insuring people whose WTP ≥ price

Socially efficient outcome: insure when π(ξi) > c(ξi)

What is the shape of AC and MC curves in the model of adverse selection?

Both downward sloping - shape driven by demand-side selection

Because higher-risk people value insurance more (higher WTP), when the price increases, low-risk people drop out and only high-risk people remain (if you go up the curve) - high risk people are more costly to insure

At any price AC>MC

What is the source of inefficiency in the model of adverse selection?

The fact that AC>MC leads to inefficiency because:

Some people have WTP > c - they value insurance more than it costs to provide - they can remain uninsured

But if WTP < p = AC they wont buy it

So we get AC > WTP > c aka there are some people that should be insured from a social efficiency point of view because WTP > c but they won’t buy it because WTP < AC/p and the market price is too high (as high-cost buyers push up the price)

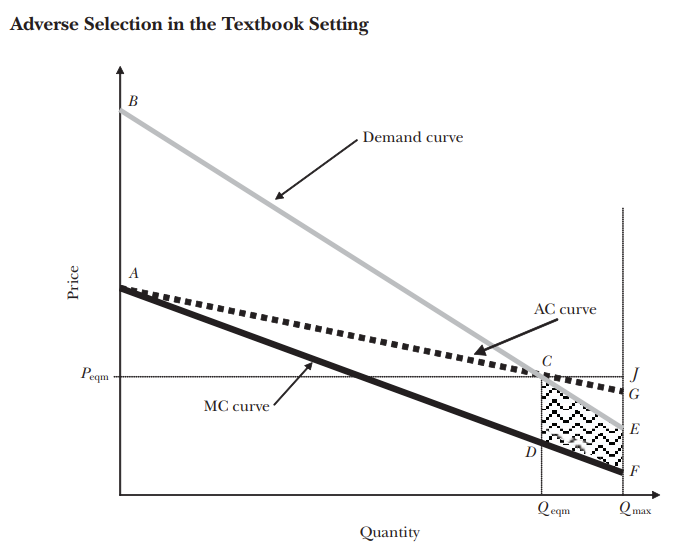
Explain this diagram.

Optimum at D=AC (perfect competition)

Efficient allocation is MC=D and equilibrium allocation is AC=D (point C)

Demand = the cumulative distribution of individuals’ WTP

Point B = highest WTP

Shaded area = Total inefficiency and the area between demand and MC after Qeq - Here WTP is greater than MC so they should be insured but are not

Peq = uniform price to everyone

Q = fraction of insured individuals

Qmax = amount of insured individuals if there is symmetric information

Qeq = equilibrium quantity

Risk premium = vertical distance between D and MC aka the WTP and expected cost - this is always positive due to risk aversion

Equilibrium quantity will always be less than the efficient quantity and the equilibrium price will always be lower than the efficient price, showing under-insurance when there is adverse selection

Welfare loss occurs since not all individuals who value insurance more than their expected cost (D/WTP > MC) get insured

Explain the downward sloping MC curve and why it represents the adverse selection property of insurance markets.

The individuals who have the highest willingness to pay for insurance are those who are expected to be the most costly for the firm to cover

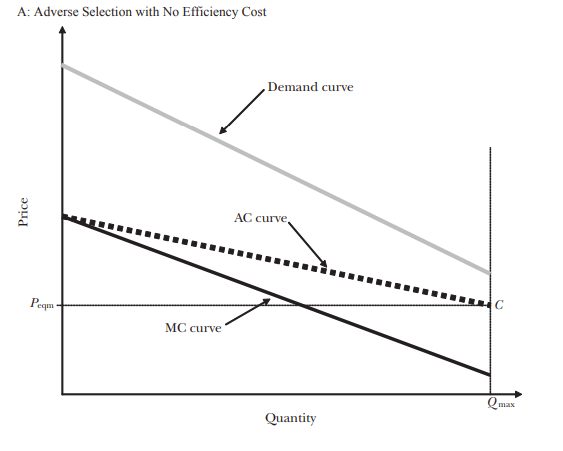
How do we draw the adverse selection model with no efficiency cost?

Unlike original diagram - just never have D and AC cross and have AC hit the Qmax line at peq

Means Qeq = Qmax

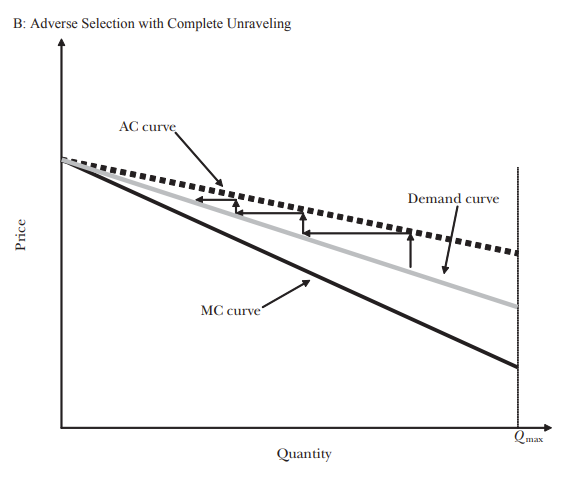
How do we draw the adverse selection model with full market unravelling?

Have AC always above demand curve

All D, MC and AC meet at one point at y axis

Individuals don’t buy if WTP<AC which is the case at all Q

What is the possible gain from government intervention in insurance markets?

Government can manipulate either equilibrium quantity or price:

• Mandating coverage: produce socially efficient outcome

  • Social efficiency gain depends on degree of under-insurance

  • Social efficiency gain but not Pareto improvement here

• Subsidizing coverage: large enough subsidy shifts demand curve out such that equilibrium closer to efficient outcome (so AC=D at closer to Qmax)

  • If marginal cost of public funds high, socially efficient subsidy may not achieve full-insurance outcome (coz would need to shift out/subsidise alot)

  • Unlikely Pareto improvement as subsidy must be paid for

How has Chiappori and Salanie (2000) tested whether adverse selection matters in practice? Are there any limitations?

Chiappori and Salanié (2000) proposed the “positive correlation” test to detect adverse selection by checking if those who buy more insurance are more likely to file claims (i.e. riskier people are more likely to buy - insurance purchase positively correlated with risk)

Limitations of this test:

• Moral hazard - Sometimes buying insurance can increase the probability of filing claims (e.g., people take more risks once insured), so the positive correlation might reflect moral hazard, not just adverse selection.

• Test only applicable in markets that exist - Many social insurance programs have no private-market counterpart, making it hard to observe what adverse selection would look like without government involvement. But Paradox: adverse selection is often used as a justification for government intervention in insurance markets but ironically, it's difficult to empirically test for adverse selection

What is the contract space?

How much coverage people can buy

What is the equilibrium defined as in the adverse selection model with endogenous contract space?

An equilibrium is a set of insurance contracts such that :

• No individual can purchase a better contract than the one they choose among those offered

• No firm has an incentive to offer a different contract than the ones offered and all firms make zero profits

What are the 2 possible types of equilibrium in the adverse selection model with endogenous contract space?

Pooling equilibrium

• One contract α BAR is offered and chosen by both types

Separating equilibrium

• Two contracts are offered α_H and α_L

• High-risk types choose contract α_H

• Low-risk types choose contract α_L

What happens in the separating equilibrium when there is symmetric and asymmetric information?

Symmetric: each type buys the contract for them at the actuarially fair price and are fully insured

Asymmetric: H type would want to buy the L contract since it is cheaper but if this happens then insurers make losses > Adverse selection problem: individuals that value insurance the most are those that are costlier to insure and firms are not able to make type-specific contracts

What happens in the pooling equilibrium in terms of the different individuals?

Low-risk L subsidises high-risk H

The average contract will be more expensive for L and cheaper for H compared to their type-specific contracts

Better for H types than if insurance actuarially fair for them

Worse for L types than if insurance actuarially fair for them

L types may still be better off than with no insurance

What are the 3 results in the adverse selection model with endogenous contract types?

1. No pooling equilibrium exists (even if both better pooling than without insurance) -

   1. Another insurer can enter and offer a different contract targeting just the low-risk (L) types—this is called “cream-skimming.”

   2. The alternative contract offers less-than-full insurance but at a cheaper premium.

   3. Only L types want to buy this because they value more the good state consumption than H types (more likely for them)

2. In any separating equilibrium, H types obtain full insurance and L types are under-insured

   1. H full insurance: No financial risk for insurers to offer this contract. “Worst case”: L types purchase it and insurers make profits

   2. L under-insured: Incentive for H types to buy L contract, but insurers would make losses in that case so, insurers offer as much insurance as possible to L types such that H types still don’t want to buy it

3. It is possible that no equilibrium exists in this market

   1. Separating could be not an equilibrium and since pooling never an equilibrium then we never have equilibrium

What would happen if governments mandate pooling contracts? Who would be better off in separating contracts?

• Both types could be better off

• Types H always benefit from pooling with less risky individuals

• Types L might be better off too when not “too many” high-risk individuals or high-risk not “too different” from low-risk individuals

• Leads to social efficiency gain and Pareto improvement

• Only types L could be better off with separating contract => In that case, social efficiency gain but not Pareto improvement

What are the 4 other motivations for social insurance?

1. Redistribution - Efficient private insurance markets imply high cost of insurance for high risk (no redistribution across types) so society might want to compensate high risk people

2. Externalities - Lack of insurance by some can impose negative externalities on others, e.g., health insurance reducing spread of communicable diseases.

3. Internalities - Individuals may not insure themselves enough against risks if the government does not force them to do so (e.g. myopia) or they might not understand complex insurance policies and make mistakes

4. Aggregate shocks - people can all be in bad state at the same time so cannot be supported by private insurance but government could have liquidity to compensate everyone at the same time