[GCE A-Levels] H2 Physics

What is the instrumental uncertainty of a digital stopwatch?

0.1 s

What is the instrumental uncertainty of a protractor reading?

1°

What is the instrumental uncertainty of a measuring reel?

1 cm

What is the instrumental uncertainty of a metre rule?

0.1 cm

What is the instrumental uncertainty of a pair of vernier calipers?

0.1 mm

What is the instrumental uncertainty of a micrometer screw gauge?

0.01 mm

In practical, you were tasked to find the length x of a string. You need to tabulate the value of ln x. What should the heading of this column be?

ln (x / m)

In practical, you were tasked to find the length x of a string. You need to tabulate the value of ln x. If the value of x was 1.2 m, what precision should the value of ln x be expressed to?

2 decimal places, because the value of x has 2 significant figures.

The gradient of a graph with axes intervals labelled is to be determined. What should be the precision of the coordinates of the two points chosen?

To half a small square.

How do you estimate the area under a graph?

Use the Trapezium Rule, or find the combined area of several triangles.

In practical, what do you write if all the data points are tightly clustered to the best fit line or curve?

There is no anomalous data as no data point deviates significantly from the trend set by all the data points, as all data points are evenly scattered about the best fit line.

What are the essential components of a practical plan?

DVARS: diagram, variables, analysis, reliability, safety

What do you need to take note of when drawing the diagram for a practical plan?

(Hint: There are 3 key things.)

1. All apparatus drawn must be clearly labelled.

2. It is necessary to include fine details (e.g. lab bench, ground) so that the apparatus set-up is not “floating in mid-air”.

3. All physical quantities to be measured (e.g. length, volume) must be indicated if possible.

What do you need to write in the variables section of a practical plan?

1. List all independent variables, and describe how it will be varied and measured.

2. List the dependent variable, and describe how it will be measured.

3. State the number of variations of the independent variable (typically 10).

4. State one or two control variables.

What do you need to write in the analysis section of a practical plan?

Provide working to show how the equation is linearised, and what graph to plot.

+

Explain how various constants can be deduced from the graph.

What do you need to write in the reliability section of a practical plan?

Include details to improve the design and/or procedure, making it more accurate and reliable. If possible, explain the rationale for these details.

+

Consider potential sources of error and how to manage or reduce them.

What do you need to write in the safety section of a practical plan?

Briefly mention a safety precaution that the experimenter should keep in mind.

State the seven base quantities and their SI base units.

mass (kg), length (m), time (s), current (A), temperature (K), amount of substance (mol), luminous intensity (cd)

What is meant by a homogeneous equation?

A homogeneous equation is one where the terms on both sides of the equation have the same units.

Distinguish between systematic and random errors in a set of measurements of a physical quantity.

Random errors are deviations of measured values from the mean values in varying signs and magnitudes.

Systematic errors are deviations of mean values from the true value in a particular sign and magnitude.

Is power a scalar or vector?

scalar

Is magnetic flux a scalar or vector?

scalar

Is magnetic flux linkage a scalar or vector?

scalar

Is potential difference a scalar or vector?

scalar

Is work a scalar or vector?

scalar

Is energy a scalar or vector?

scalar

Is pressure a scalar or vector?

scalar

Is electric current a scalar or vector?

scalar

Is activity a scalar or vector?

scalar

Is acceleration a scalar or vector?

vector

Is torque a scalar or vector?

vector

Is field strength a scalar or vector?

vector

Is magnetic flux density a scalar or vector?

vector

The percentage uncertainty of a measurement of length L = 3.50 m is 1%. What is the actual uncertainty?

0.04 m (1 s.f.)

If R = kA^mBⁿ, then how can we find 𝛥R?

𝛥R/R = |m| 𝛥A/A + |n| 𝛥B/B

Define Precision.

A measure of the degree of consistency and agreement between independent measures of the same quantity.

Define Accuracy.

A measure of the closeness of agreement between measured values and the true value.

The relative vector of A with respect to B is…

v_A – v_B

Express 1 tesla in SI base units.

1 kg s^-2 A^-1

Express 1 ohm in SI base units.

1 kg m² s^-3 A^-2

Express 1 volt in SI base units.

1 kg m² s^-3 A^-1

Express 1 Pa in SI base units.

1 kg m^-1 s^-2

Express 1 Bq in SI base units.

1 s^-1

Express 1 weber in SI base units.

1 kg m² s^-2 A^-1

Define acceleration of an object.

Acceleration is the rate of change of velocity with respect to time.

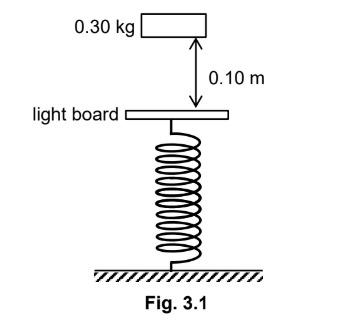
Refer to Fig. 3.1.
How to calculate the maximum compression of the spring in this scenario?

loss in GPE = gain in elastic PE

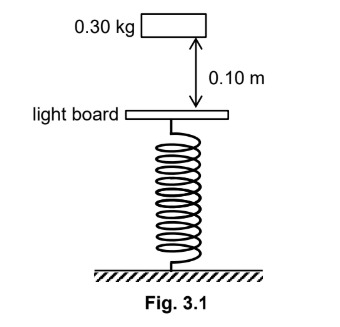
Refer to Fig. 3.1.
How to calculate the maximum KE attained by the block?

Maximum KE attained when velocity is maximum. This occurs when acceleration is zero.

Thus maximum KE occurs when mg = kx.

Express 1 J in SI base units.

1 kg m² s^-2

Express 1 W in SI base units.

1 kg m² s^-3

State the equations of motion.

What is a critical assumption made when applying these equations?

The equations are:

• v = u + at

• s = ut + ½ at²

• s = ½ (u+v)t

• v² = u² + 2as

They are only applicable when acceleration a is constant.

What is meant by a free-falling body?

A free-falling body is one that moves only under the influence of gravity.

The only force acting on a free-falling body is its weight, and its acceleration is g by Newton’s 2nd Law.

Describe the motion of a free-falling body.

For a body falling in air and subject to air resistance, its initial acceleration is g (since when v = 0, there is no viscous drag force).

Thereafter, a decreases in magnitude as F_D increases.

Eventually, if the body falls over a sufficient distance, a = 0 and the body reaches terminal velocity.

The path of projectile motion assuming negligible air resistance is…

a parabolic trajectory

An object set in projectile motion with air resistance. How will its path compare to one without air resistance?

State all differences.

1. The trajectory is not parabolic.

2. The trajectory is not symmetrical about the highest point.

3. The time taken to travel up is less than the time taken to travel down.

4. The horizontal range is shorter.

5. The vertical range is lower.

Explain fully why the time taken to travel up is less than the time taken to travel down for projectile motion with air resistance.

Vertically, on the flight up, both weight and air resistance act downwards, so the magnitude of net force is larger and the magnitude of net acceleration is more than g.

On the flight down, weight acts downwards but air resistance acts upwards, so the magnitude of net force is smaller and the magnitude of net acceleration is less than g.

Since the distance travelled up is equal to the distance travelled down, the time taken to travel up is lower than the time taken to travel down.

When drawing a free-body diagram, what is the point of action of tension?

end of string or rope being pulled taut

When drawing a free-body diagram, what is the point of action of normal contact force?

surface of contact

When drawing a free-body diagram, what is the point of action of weight?

centre of gravity of body

When drawing a free-body diagram, what is the point of action of upthrust?

centre of gravity of displaced fluid

When drawing a free-body diagram, what is the point of action of friction?

surface of contact

Define friction.

Friction is the force that resists the relative motion or the tendency for relative motion between two surfaces that are in contact.

Define normal contact force.

Normal contact force is the net electrostatic repulsion between two surfaces that are in contact.

Define tension.

Tension is the force exerted by one end of a string that is being pulled taut.

Try this question and explain your answer.

Answer: (C) 4

Consider the six cases of 𝛥E of X.

Define upthrust.

Upthrust is the net upward force exerted by a fluid on an object partially or fully submerged in it.

Define centre of gravity.

The centre of gravity is the point at which the weight of a body appears to act.

Explain fully why an object is more stable when its centre of gravity is lowered.

This is because the forces acting on the body will form a restoring couple to return the system to equilibrium.

State Newton’s First Law of Motion.

Newton’s 1^st Law of Motion states that an object stays at rest or continues to move with a constant velocity in a straight line unless a net external force acts on the object.

State Newton’s Second Law of Motion.

Newton’s 2^nd Law of Motion states that the rate of change of linear momentum of an object (with respect to time) is directly proportional to the net force acting on it, and is in the same direction as the net force.

State Newton’s Third Law of Motion.

Newton’s 3^rd Law of Motion states that if body A exerts a force on body B, then body B exerts a force on body A that is equal in magnitude and opposite direction.

If body A is on top of body B, what is the main force that connects both bodies?

friction

Define the linear momentum of an object in motion.

Linear momentum is the product of the mass of an object and its velocity.

State the Principle of Conservation of Linear Momentum.

The Principle of Conservation of Linear Momentum states that if no net external force acts on a system, the total momentum of the system remains unchanged.

Define Impulse.

Impulse refers to the product of the average net force acting on an object and the time interval over which this force is applied.

What is the relationship between impulse and momentum?

The Impulse-Momentum theorem states that the impulse acting on an object during a time interval is equal to its total change in momentum during the same time interval.

Distinguish between a head-on collision and a glancing collision.

A collision is head-on if the directions of motion before and after the collision are along the same line of motion.

On the other hand, a collision is glancing if the directions of motion before and after the collision are not along the same line of motion.

What does it mean if a collision is elastic?

A collision is elastic if 100% of the kinetic energy is conserved.

However, some of the KE may be temporarily converted to PE during the collision.

What does it mean if a collision is inelastic?

A collision is perfectly inelastic if the maximum amount of kinetic energy is lost, without violating the Principle of Conservation of Linear Momentum.

Colliding objects coalesce with each other and travel at the same velocity after the collision.

What is a common formula used for elastic collisions?

For elastic collisions, the relative speed of approach is equal to the relative speed of separation.

State Hooke’s Law.

Hooke’s Law states that the magnitude of the force exerted by a spring on a body attached to the spring is directly proportional to the extension or compression of the spring from its natural length, provided the proportionality limit of the spring is not exceeded.

What is the formula for the pressure due to a fluid?

Hence, state the formula for total pressure experienced.

The pressure due to a fluid is 𝜌gh,

so the total pressure is 𝜌gh + P_atm.

State Archimedes’ Principle.

Archimedes’ Principle states that the upthrust acting on an object partially or fully submerged in a fluid is equal to the weight of fluid displaced.

(U = 𝜌Vg)

Define torque due to a force.

Torque refers to the product of the magnitude of force F and the perpendicular distance from the pivot to the line of action of the force.

(𝜏 = Fr sin 𝜃)

Explain the origin of upthrust.

Pressure increases with depth.

When an object is partially or fully submerged in a fluid, since pressure is average force per unit area, the force acting on the bottom part of the object is greater than the force acting on the top part of the object.

Hence, there is a resultant force directed upwards, which is termed upthrust.

State the Principle of Moments.

The Principle of Moments states that for a body to be in rotational equilibrium, the sum of the clockwise moments must be equal to the sum of the anticlockwise moments about any point.

State the three types of equilibrium possible for a system, and the physical interpretation of each.

An object is in translational equilibrium if the net external force acting on it is zero.

An object is in rotational equilibrium if the net torque about any point is zero.

An object is in static equilibrium if it is both in translational and rotational equilibrium.

For a three-force system in equilibrium…

the lines of action of the forces must either be parallel or pass through a common point.

What is meant by a couple?

State the torque created by a couple.

A couple is a pair of forces that are equal in magnitude, opposite in direction, and their lines of action do not coincide. A couple produces rotation only and no translation.

The torque of a couple is F × d, where d is the perpendicular distance between the two parallel forces.

Define work done by a force.

Work done by a force is the product of the magnitude of the force and the magnitude of the displacement of the body in the direction of the force.

(W = Fs cos 𝜃)

What does the work-energy theorem state?

The Work-Energy theorem states that the net work done on an object is equal to its change in KE.

State the formula for the kinetic energy of an object,

and derive it.

The kinetic energy of an object is given by E_k = ½mv².

• Exert a force F on a body initially at rest. Let its displacement, in the same direction, be s.

• Then, KE = work done = Fs = mas = m(v²/2) = ½mv².

State the formula for the gravitational potential energy of an object near the surface of the Earth,

and derive it.

The gravitational potential energy of an object near to the surface of the earth is E_p = mgh.

• Vertically lift a stationary body of mass m, artificially keeping it stationary.

• Since velocity is constant (at zero), there is no acceleration. Hence, F = mg.

• Then, GPE = work done = Fs = (mg)(h) = mgh.

What is the formula associated with a conservative force and its associated potential energy?

State a key significance in the relation.

For any conservative force, F = –dU/dx where U is the associated potential energy.

The negative sign in the relation suggests that the force acts in the direction of decreasing potential energy.

Suppose work is done on a spring. What can be said about the value of elastic potential energy?

It increases.

Suppose work is done by a spring. What can be said about the value of elastic potential energy?

It decreases.

State the formula for the elastic potential energy of a spring,

and derive it.

The elastic potential energy of a spring is E_k = ½kx²:

• Suppose the spring is extended or compressed from its original length.

• Then, EPE = work done = area under F-x graph = ½Fx = ½kx², by applying Hooke’s Law.

State the Principle of Conservation of Energy.

The Principle of Conservation of Energy states that energy can be converted from one form to another, but cannot be created or destroyed.

What is meant by power?

What is another formula associated with power?

Power is the rate at which work is done, so P = dW/dt.

It can also be derived that P = Fv at any instant, and also when taking the average over a time interval.

How can the efficiency of an energy conversion be calculated?

The efficiency of an energy conversion is the ratio of useful energy output to total energy input,

or the ratio of useful power output to total power input.

Define the radian.

One radian is the angle subtended at the centre of a circle by an arc equal in length to its radius.