1.4 unit deductive & inductive reasoning.

1.4 unit deductive & inductive reasoning.

reasoning

• way of thinking guided by a series of systematic rules.

• all reasoning is thought, but not all thought is reasoning.

• allows individuals to draw conclusions from premises or prior information

• provides us with new knowledge based on the relationships we establish between what we already know

• mental activity for processing information, which underlies thought

• Involves making inferences & an inference is the process of moving from certain beliefs to other beliefs

What is reasoning & inferring

• psychological processes for revising or maintaining beliefs, plans or intentions

Final definition of reasoning

• process through which we obtain unknown knowledge from known facts

Key elements within reasoning 

• Premises

• Conclusions

• Argument or statement

• Inferential process

Premises

• These are the propositions or statements from which we begin (known information).

• When related to each other, they allow us to reach an unknown conclusion or new information.

Conclusions

• information derived from the relationship between the premises.

• Conclusions are not explicitly stated in the premises content but are inferred from them.

Argument or statement

• consists on both premises & conclusions.

• An argument can be valid or invalid.

• A valid argument is one where a conclusion (x) can be reached from a series of premises (P1, P2 ... Pn.).

inferential process

• method used to derive or reach the conclusion from the premises. 

• can be categorized into deductive reasoning & inductive reasoning

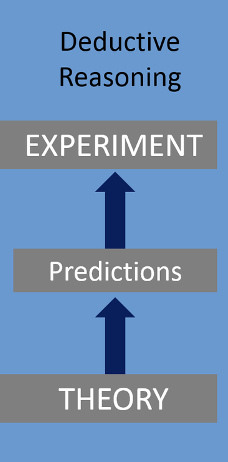
Deductive Reasoning

• allows individuals to reach a conclusion based on previous information

• ensuring that if the premises are true

• the conclusion cannot be false.

• linked to formal logic & the application of its rules.

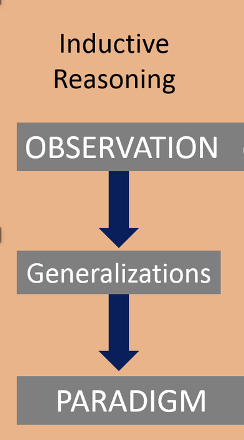
Inductive Reasoning

• allows individuals to reach a probable conclusion based on the observation of a phenomenon, or previous experience.

• conclusions cannot be generalized to all related cases of the same phenomenon.

Inductive reasoning relation to the key elements

• generating new knowledge from previous experiences

• The premises of an inductive argument do not prove the conclusions (they only support)

• moves from the specific to the general.

• is essential for developing principles, theories and laws

• “bottom-up” argument

  

Deductive reasoning relation to the key elements

• determining whether the conclusion logically follows from the starting premises

• focuses on the rules of thought regardless of content

• move from the general to the specific and concrete.

• does not generate new truths.

• top-down” argument

• 

Benefits with deductive & inductive reasoning

• constant interplay between inductive inference (based on observations) & deductive inference (based on theory), until we get closer and closer to the 'truth

• Deductive reasoning establishes → connection between theory and observation allowing us to deduce phenomena from the theory.

• Inductive reasoning → accumulation of knowledge

SOUND

• used instead of "solid" because in logic and philosophy

• “soundness”

to be SOUND → it has to meet two criteria

• argument is valid

• premises are true

argument is valid

The conclusion logically follows from the premises.

premises are true

The content of the premises is factually correct.

sound argument

is both logically valid & factually correct.

SOLID VS SOUND

• SOLID → more general term describes something reliable or strong, less logical.

• sound → assess the quality of arguments in formal reasoning.

Quality of an argument is determined by two factors

• Truth or falsehood of the reasoning

• Validity or invalidity of the reasoning

Truth or falsehood of the reasoning

• The content of both the premises & the conclusions can be either true or false

• The facts you are using to prove your point

example of a false premise

• We all learn at the same speed.

• (We know this isn’t true, so if your argument is based on this, it`s not a solid start).

Validity or invalidity of the reasoning

• refers to the form or structure of the argument, not the content

• How well do your ideas connect

• Does the conclusion logically follow from the premises –the reasons you gave

example of invalid reasoning

• P1. Footballers make a lot of money.

• P2. Messi is a footballer.

• Conclusion: Messi is a PSG player

reasoning vs conclusion

• While the content of both the premises and the conclusion may be true → the reasoning is invalid because the conclusion does not logically follow from the premises.

sound argument

the arguments are both true & valid

Suppes & Hill

• thought consists of a series of inference rules that allow us to obtain valid deductive arguments

• Modus Ponens

• Modus Tollens 

• Law of hypothetical syllogism

• Law of Disjunctive Syllogism

Modus Ponens

• is used to confirm the hypothesis by allowing us to reach a probable logical conclusion based on the premises.

• 

Modus Ponens

Abstract formulation

• P1. If (p) is true, then (q) is also true.

• P2. (p) is true

• Conclusion: I deduce that (q) is also true

Example of MODUS PONENS

•P1. If a child pays attention in class (p), then they will learn (q).

•P2. Louis pays attention in class (p).

•Conclusion: I deduce that Louis will learn (q).

Modus Tollens

• used to refute a hypothesis

• 

Modus Tollens

Abstract formulation

• P1. If (p) is true, then (q) is also true.

• P2. (q) is not true.

• Conclusion: I deduce that (p) is not true either.

Example of modus tollens

•P1. If a child pays attention in class (p), then they will learn (q).

•P2. Louis has not learned (not q).

•Conclusion: I deduce that Louis did not pay attention (not p). 

Law of hypothetical syllogism

Abstract formulation

•P1. If (p) is given, then (q) is also given.

•P2. If (q) is given then (r) is also given.

•Conclusion: I deduce that if (p) is given then (r) is also given.

 

Example of Law of hypothetical syllogism

• P1. If I prepare the class well (p), then the students will pay more attention (q).

• P2. If students pay more attention (q), then it is easier for them to learn (r).

• Conclusion: I deduce that if I prepare the class well (p), then it will be easier for students to learn (r).

Law of Disjunctive Syllogism

Abstract formulation

•P1 It is given (p) or it is given (q).

•P2. If (p) is given, then (r) is given.

•P3. If (q) is given, then (s) is given.

•Conclusion: I deduce that (r) o (s) is also given.

example of Law of Disjunctive Syllogism

•P1. Tonight it may rain (p) or it may not rain (q).

•P2. If it rains (p), then I stay home (r).

•P3. If it doesn't rain (q), then I go to the cinema (s).

•Conclusion: Tonight I either stay home (r) or go to the cinema (s).

Inductive reasoning

• reasoning involves identifying patterns and regularities in the environment

• allows us to extrapolate and generalize past experiences to future ones, with some degree of uncertainty.

David Hume & Mill

• set of rules for determining causal relationships

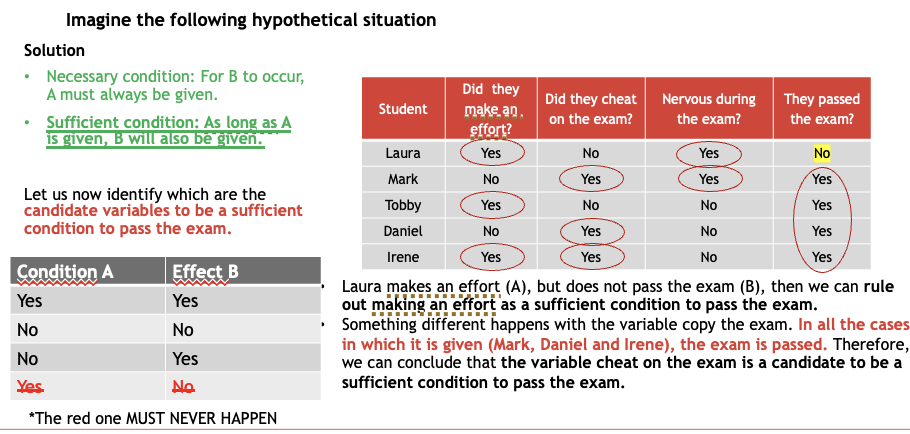
• to determine whether a cause is sufficient, necessary, or both sufficient and necessary to produce a given effect

• there is information about the presence or absence of other causes & the presence or absence of the effect in these situations

Mills method

• help determine whether a cause sufficient and/or necessary for the occurrence of an effect

• Necessary

• Sufficient

• Both sufficient and necessary

Necessary

• the effect cannot occur without it.

• B can not occur without A

• Something MUST be present for the effect to occur

Sufficient

• presence GUARANTEES the effect, but the effect can still occur through other means

Both sufficient and necessary

• only cause that ensures the effect

Elements of Mill´s method

• Conditioned property (E)

• Conditioning properties (candidate variables)

• → This analysis is done by examining situations where the causes & effects are either present or absent to draw conclusions about their relationship.

Conditioned property (E)

• the property or effect being analysed

Conditioning properties (candidate variables)

• properties that are necessary or sufficient conditions for a conditioned property.

How do we determine which conditions are sufficient and/or necessary?

• Eliminated based on two principles:

• necessary condition

• ufficient condition

necessary condition

• cannot be absent when the effect is present

• the necessary variable is required

• something must be PRESENT for the effect to occur

Necessary condition photo

Any property that is absent when the effect is present cannot be a…

necessary effect

Example of necessary condition

without oxygen, fire cannot exist

Sufficient condition

• cannot be present when the effect is absent

• Effect can appear both with or without sufficient variable 

• if present, GUARANTEES the effect, but the effect can still occur through other means.

Sufficient condition photo

Any property that is present when the effect is absent cannot be a…

Sufficient effect

Example of sufficient condition

Striking a match is a sufficient condition for fire, but fire can also be created by other means.

How do we figure out which conditions are necessary or sufficient? 

• look at the instances where the effect occurs and doesn’t occur, & systematically eliminate variables that don’t meet these criteria

Steps when analysing causes & effect

1. Define the Effect

2. Identify Candidate Variables (list up variables that might influence the effect)

3. Collect Data (might include cases where effect is present or absent)

4. Apply the Principles:

- Necessary Condition Principle: if the effect is ever present without the candidate variable

- Sufficient Condition Principle: if the candidate variable is present when the effect is absent.

5. Analyse and Eliminate

- For Necessary Conditions: Eliminate candidate variables that are absent when the effect occurs

- For Sufficient Conditions: Eliminate candidate variables that are present when the effect does not occur

6. Test for Both Necessary and Sufficient Conditions Determine if any variables can be classified as both necessary and sufficient

7. Refine and Validate Reevaluate the candidate variables and their relationships with the effect based on the data collected

Errors and biases in DEDUCTIVE reasoning are due to two factors

1. Difficulty in understanding the logical structure underlying the problem.

2. Misinterpretation of the content.

frequent errors in inductive reasoning

• related to our cognitive limitations when dealing with a large amount of information.

• we commonly use heuristics (cognitive shortcuts) that guide our judgment → which can lead to systematic errors. 

Errors and biases in deductive reasoning (AFFIRMING)

Errors and biases in deductive reasoning (DENYING)

CONCLUSION of deductive & inductive reasoning 

• Reasoning is a cognitive process that underpins thought. It allows us to derive new information from known facts by applying a series of rules.

• Deductive reasoning ensures that we obtain valid conclusions from true premises.

• Inductive reasoning allows us to generalize from past experiences & reach conclusions that are more or less probable.

• Formal logic determines whether we have correctly applied the rules underlying deductive reasoning.

• When applying inductive reasoning to draw conclusions, we can identify necessary & sufficient conditions.

• The most frequent errors or biases in deductive reasoning are mainly due to:

1. Difficulty in understanding the logical structure &

2. Erroneous interpretation of the content.

• The most frequent errors or biases in inductive reasoning stem from limitations in our cognitive capacity, which lead us to apply heuristics or cognitive shortcuts that are not always reliable.

Modus Ponens is used to

• confirm the hypothesis by allowing us to reach a valid conclusion.

Modens Tollens is used to

refute the hypothesis.