Gravitational Field Equations

Kepler’s 3rd Law

\frac{GMm}{r^2}=\frac{mv^2}{r}

What is the symbol for the universal gravitational constant, and what is its value and SI unit?

G, 6.67 × 10¹¹ NM²/kg²

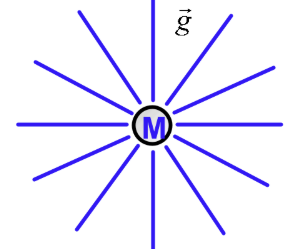
g is now being redefined from gravitational acceleration to the gravitational field - it is a vector field, as shown by the image.

Thus, g_r = ___ = ___

F_g, GM / r²

W (weight) = ___ = ___

F_g or mg, GMm / r²

If you want to find the gravitational field (g_r) of a uniform thin spherical shell, you use the equation:

g_r = ____ for r\ge R

g_r = ____ for r<R

-GM / r², 0

Gauss’ Law for Gravity states that…

g_r = ____ for r\ge R

g_r = ____ for r<R

-GM / r², 0

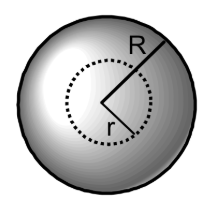
A solid sphere of radius R would have an infinite number of uniform thin spherical shells inscribed inside. Each shell has a gravitational field outside of it that depends only on its mass.

Thus, let’s say the mass within the sphere of radius r is defined as m.
The mass of the sphere of radius R is defined as M. The gravitational field at r is due solely to the mass within the smaller field.

What’s the equation for m?

m=\frac{Mr^3}{R^3}

The gravitational force (g) of a solid sphere:

g_r = ____ for r\le R

g_r = ____ for r\ge R

And then what happens when r = R?

-GMr / R³, -GM / r²

The two values for g_r are equal for r = R.