Calculus 2 Final Exam Review

McLaurin Series for 1/(1-x)

∑xⁿ=1+x+x²+x³+x⁴+...

R=1

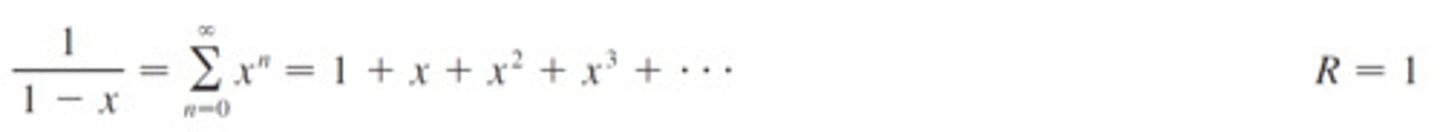
McLaurin Series for e^x

∑xⁿ/n!=1+x/1!+x²/2!+x³/3!+...

R=infinity

McLaurin Series for sinx

∑(-1)ⁿ(x²ⁿ⁺¹)/(2n+1)!=x-x³/3!+x⁵/5!-x⁷/7!+...

R=infinity

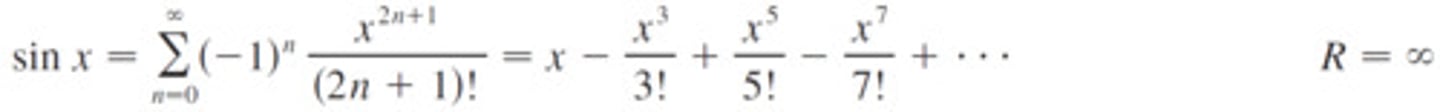
McLaurin Series for cosx

∑(-1)ⁿ(x²ⁿ)/(2n)!=1-x²/2!+x⁴/4!-x⁶/6!+...

R=infinity

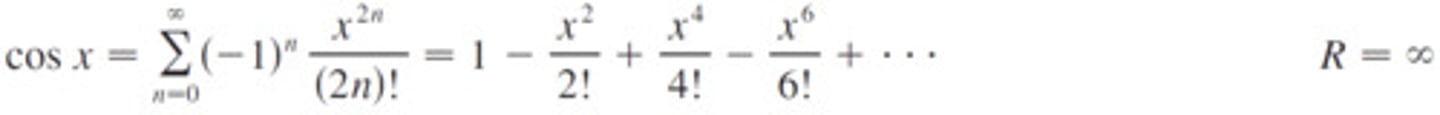
Conditionally Convergent

A series is ∑ a_n is called conditionally convergent if it is convergent but not absolutely convergent.

Absolutely Convergent

A series ∑ a_n is called Absolutely convergent if the series of absolute values ∑ |a_n| is convergent

also if the series is absolutely convergent it is also convergent.

Root Test

L=1 (nothing) L<1 (converges) L>1 (diverges)

Ratio Test

L=1 (nothing) L<1 (converges) L>1 (diverges)

The Alternating Series Test

Integral Test

Surface Area

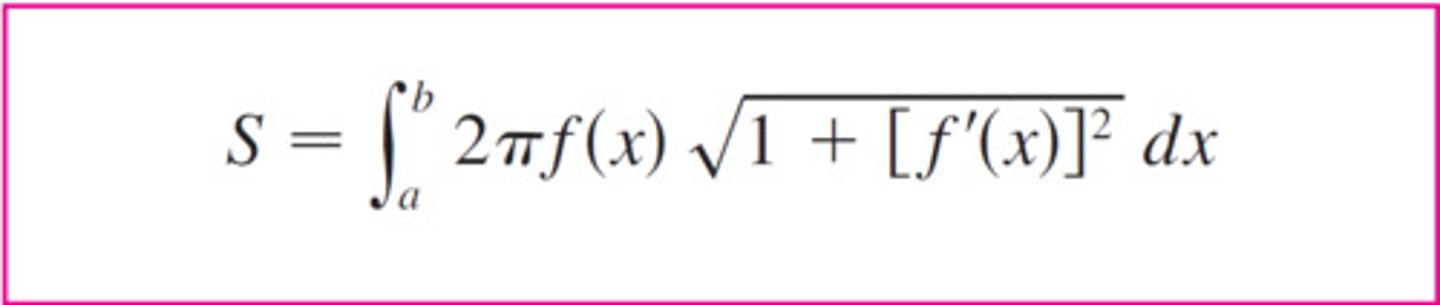
Limit Laws for Sequences

Geometric Series

Divergence Test

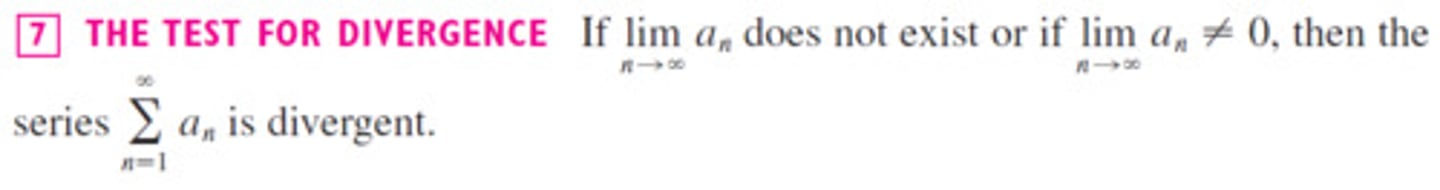
P-Series Test

SA Rotation about x-axis

f(x)

SA Rotating about y-axis

x

Alternating Series Estimation

Integral Test Remainder Estimate

For integral remainder 1/sqru(n^4+1) < 1/Sq(n^4) = 1/n^2

take integral of last one and b=inf and a=10

The Comparison Test

(i) If ∑bn is convergent and an≤bn for all n, then ∑ an is also convergent.

(ii) If ∑bn is divergent and an≥bn for all n, then ∑ an is also divergent

.

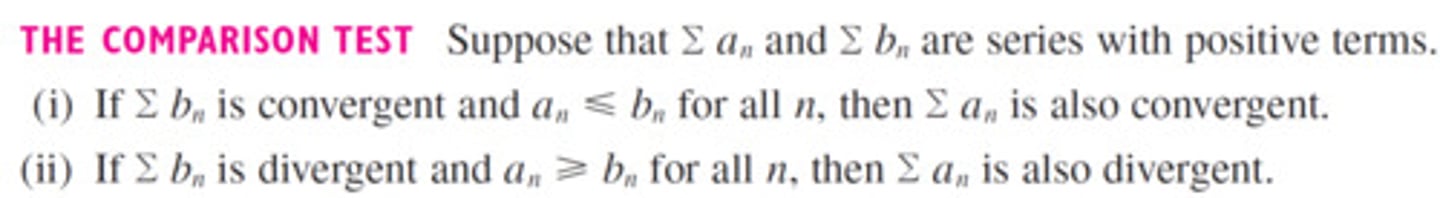
practice prob

Washer Method

pi∫(outer radius)²-(inner radius)²

(x-axis)

Shell Method

2pi∫rh

(y-axis)

Integration by Parts

uv-∫vdu

Arc Length Formula

∫√(1+(dy/dx)^2)

∫lnu

ulnu-u

sin2x

2sinxcosx

sin²x

(1-cos2x)/2

cos²x

(1+cos2x)/2

∫secxdx

ln|secx+tanx|

Derivative of secx

secxtanx

Derivative of tanx

sec²x

Derivative of cscx

-cscxcotx

Derivative of cotx

-csc²x

SA Rotating about y-axis

x

Length of Polar Curve

∫√(r²+(dr/d∅)²)d∅

derivative of sinx

cosx

derivative of cosx

-sinx

integral of sinx

-cosx

integral of cosx

sinx

Sin(A) Sin(B)

1/2[Cos(A-B)-Cos(A+B)]

Cos(A) Cos(B)

1/2[Cos(A-B)+Cos(A+B)]

Sin(A) Cos(B)

1/2[Sin(A-B)+Sin(A+B)]

f average

(1/B-A)∫f(x)dx

Area

b

∫[f(x)-g(x)]dx

a

√(a²-x²)

x=aSinθ

√(x²-a²)

x=aSecθ

√(a²+x²)

x=aTanθ

Limit Laws for Sequences

Surface area

b

S=∫ 2π f(x) √(1+[f'(x)]²) dx

a

Integral Test

Integral Test Remainder Estimate

Absolutely Convergent

A series ∑ a_n is called Absolutely convergent if the series of absolute values ∑ |a_n| is convergent

also if the series is absolutely convergent it is also convergent.

Conditionally Convergent

A series is ∑ a_n is called conditionally convergent if it is convergent but not absolutely convergent.

Limit of arctan(n)

n-->∞

π/2