3.5 Kinetic Molecular Theory

A simplified model that describes the nature of gases.

Kinetic Molecular Theory

Abbreviation of Kinetic Molecular Theory:

KMT

A series of postulates that are based on speculations about the behavior of each gas particle.

Kinetic Molecular Theory

Postulate 1 of Kinetic Molecular Theory:

The size of a gas particle is so small compared with the distances between the particles that the volume of the particles is negligible, that is to say, it is so small that the volume of the gas particles can be ignored.

Postulate 2 of Kinetic Molecular Theory:

Gas particles are in constant, random motions. They move in straight lines until they bump into each other or the walls of the container. When the particles bump into the walls of the container this results in the phenomenon that we call gas pressure.

Postulate 3 of Kinetic Molecular Theory:

The particles are assumed to have no attractive or repulsive forces between them, in other words, the effect of IMF can be ignored (for an “ideal” gas)

Postulate 4 of Kinetic Molecular Theory:

The average kinetic energy of a sample of a gas is proportional to the Kelvin temperature of the gas. (KE =1⁄2 mv² OR Kinetic Energy is equal to 1⁄2 x mass x velocity squared)

Over the years, what have scientists done with gases?

Studied them and noted how they act under different circumstances

There are several gas laws that look at:

How one variable changes when another is varied

What are the 4 gas laws?

Boyle’s law, Charles’ Law, Gay-Lussac’s Law, Avogadro’s Hypothesis

Boyle’s law is relationship between:

Pressure and volume

Boyle’s law equation:

P1V1 = P2V2

Mathematical relationship of Boyle’s law:

Inverse

Charles’ law is relationship between:

Volume and temperature

Charles’ law equation:

V1/T1 = V2/T2

Mathematical relationship of Charles’ law:

Direct

Gay-Lussac’s law is relationship between:

Pressure and temperature

Gay-Lussac’s Law Equation:

P1/T1 = P2/T2

Mathematical relationship of Gay-Lussac’s Law:

Direct

Avogadro’s hypothesis is relationship between:

Volume and number of moles

Avogadro’s hypothesis equation:

V1/n1 = V2/n2

Mathematical relationship of Avogadro’s hypothesis:

Direct

By combining the 4 gas laws, we get:

Combined gas law

Combined gas law equation:

(P1V1)/(n1T1) = (P2V2)/(n2T2)

A Maxwell-Boltzmann distribution shows:

The distribution of the kinetic energies of particles at a given temperature

As you look at the Maxwell-Boltzmann distribution you can see that it skews to the:

Right

Maxwell-Boltzmann distributions being skewed to the right means that:

The tail on the right is longer

At the origin on a Maxwell-Boltzmann distribution, the speed is:

Zero

Why is speed zero at the origin on a Maxwell-Boltzmann distribution?

Speed can’t be less than zero

Draw a Maxwell-Boltzmann Distribution

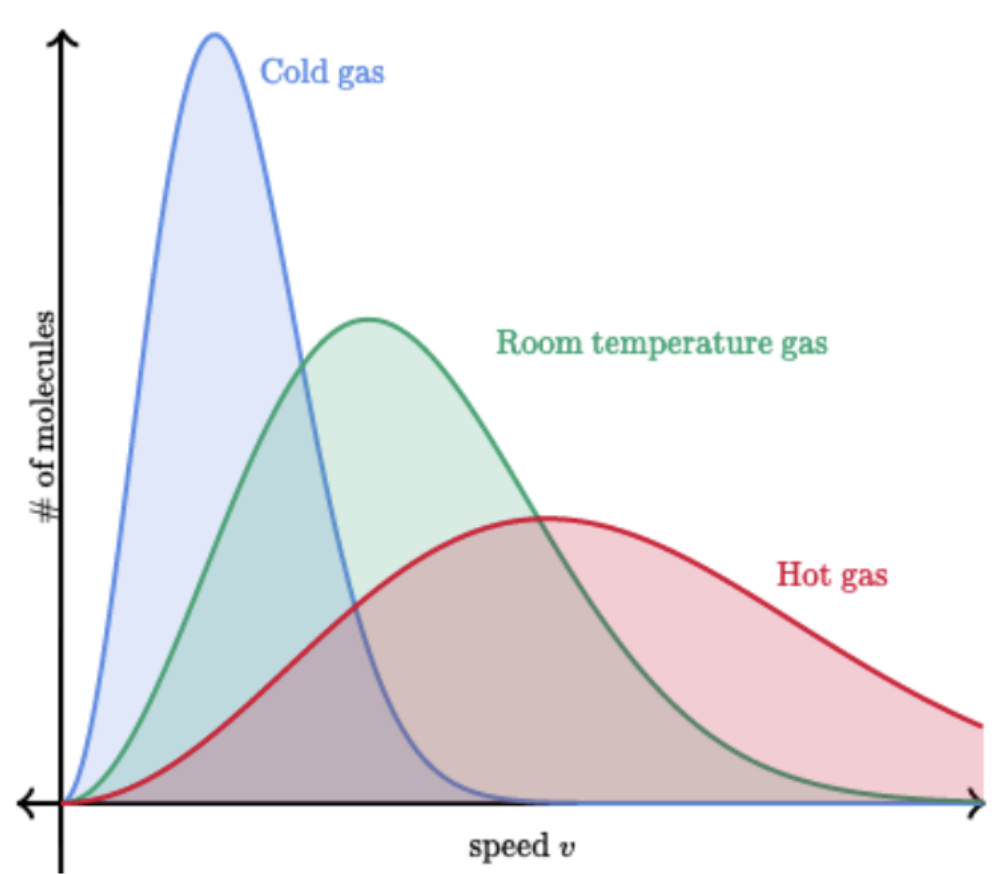
On a Maxwell-Boltzmann distribution, by increasing the temperature of a gas the distribution of the particle shifts to the:

Right

Does every particle have the same energy?

No

The temperature measures:

An average of the kinetic energy of the particles

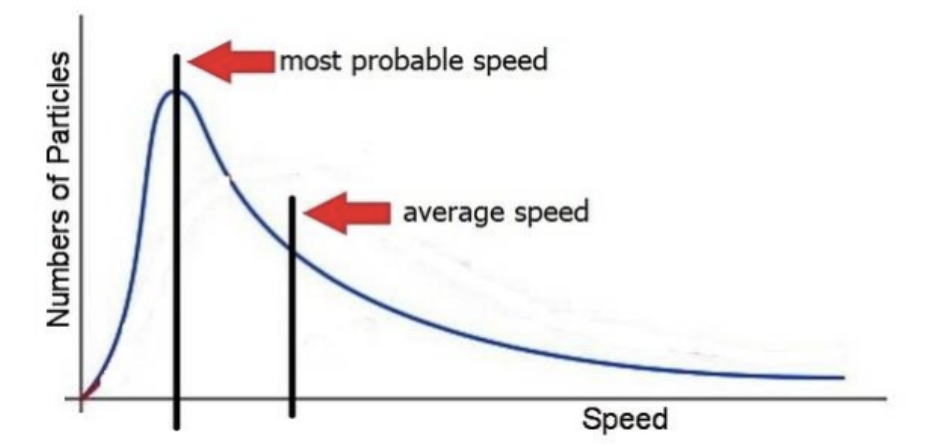
Label the most probable speed and average speed on a Maxwell-Boltzmann Distribution

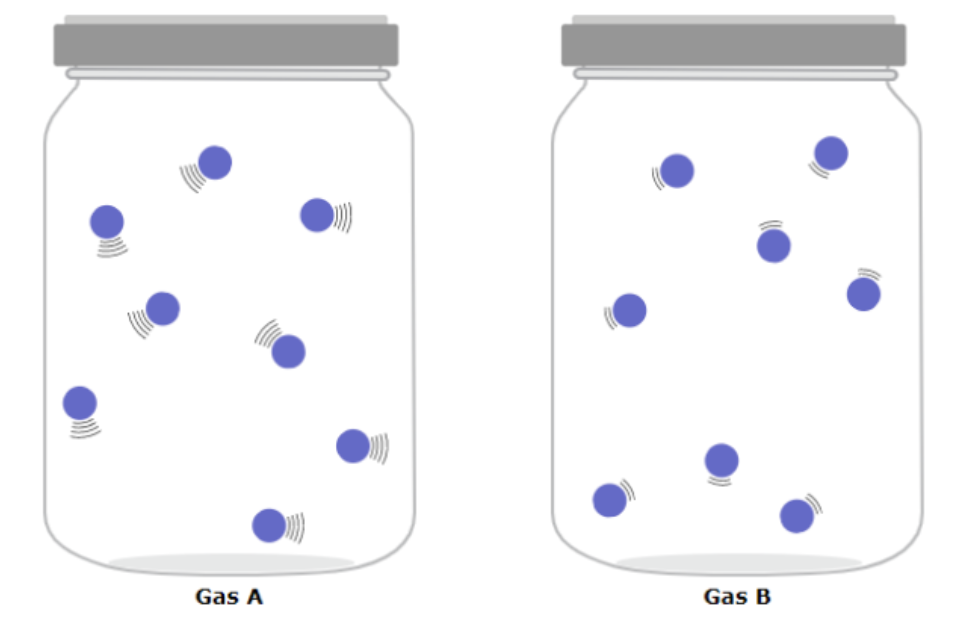
Compare temperatures of first and second gases

First gas has greater temperature

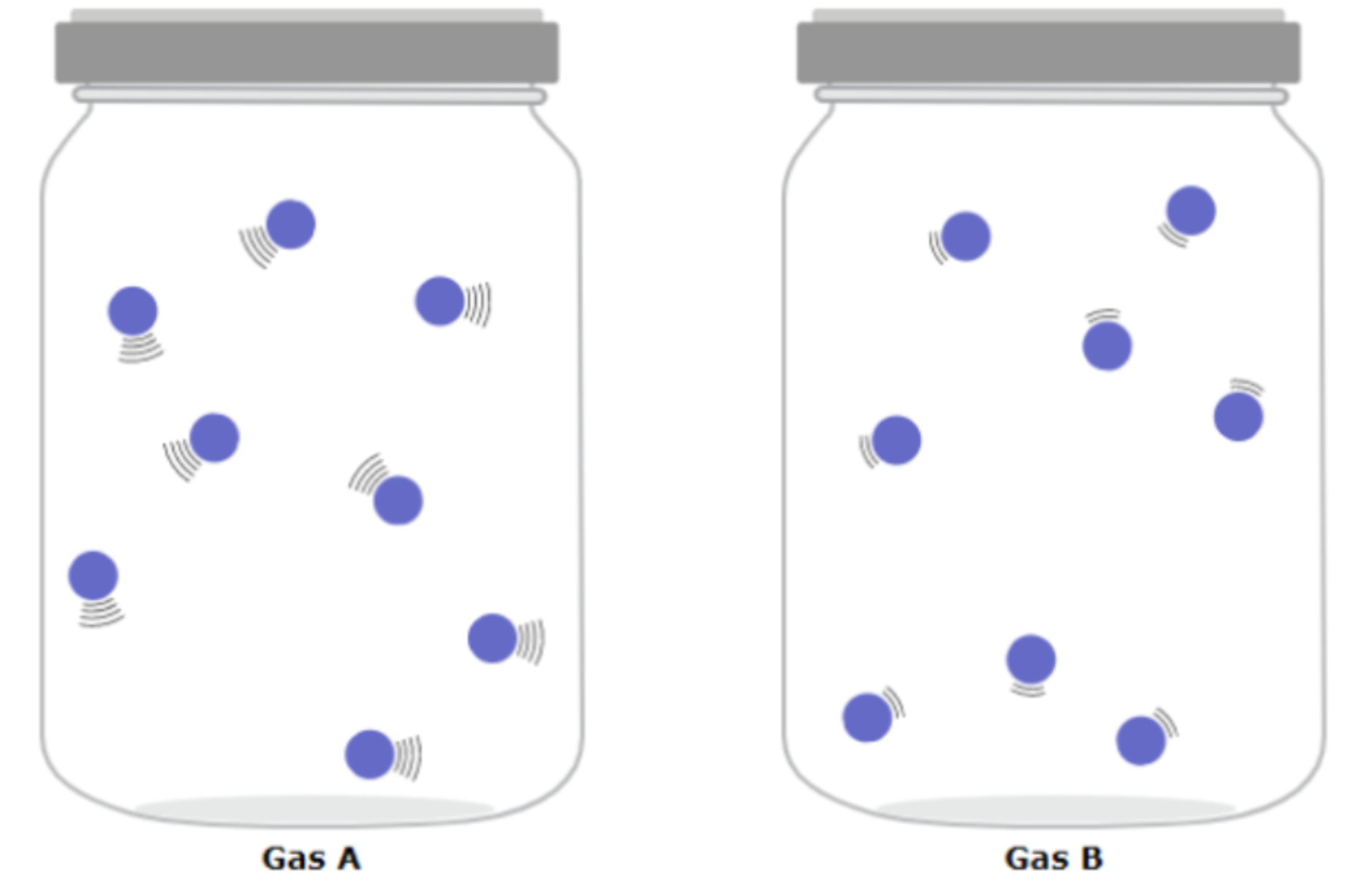
Compare masses of first and second gases

Same

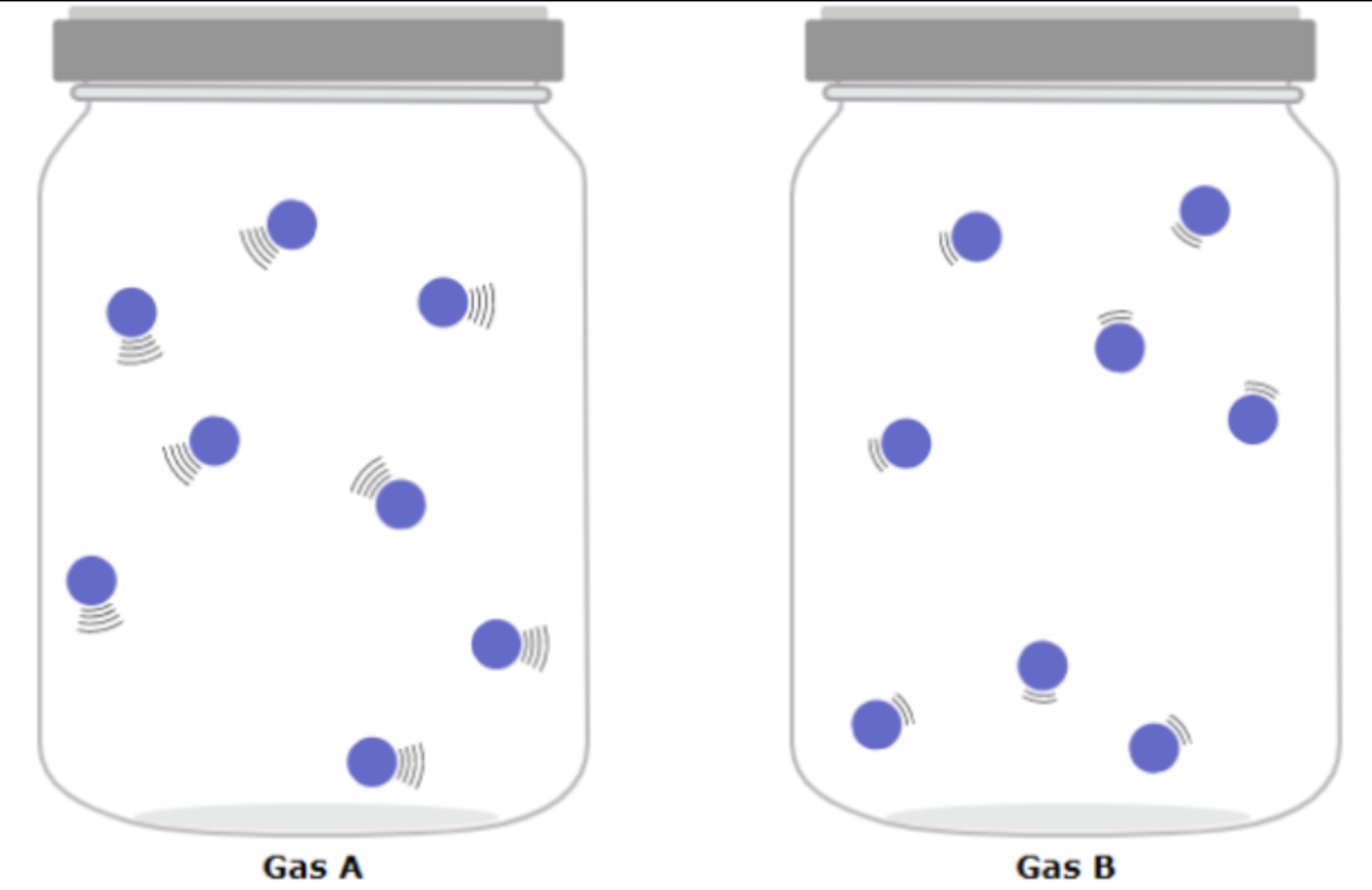
Is the kinetic energy of the two gases same or different and why or why not?

Differnet because mass is same but velocity differs

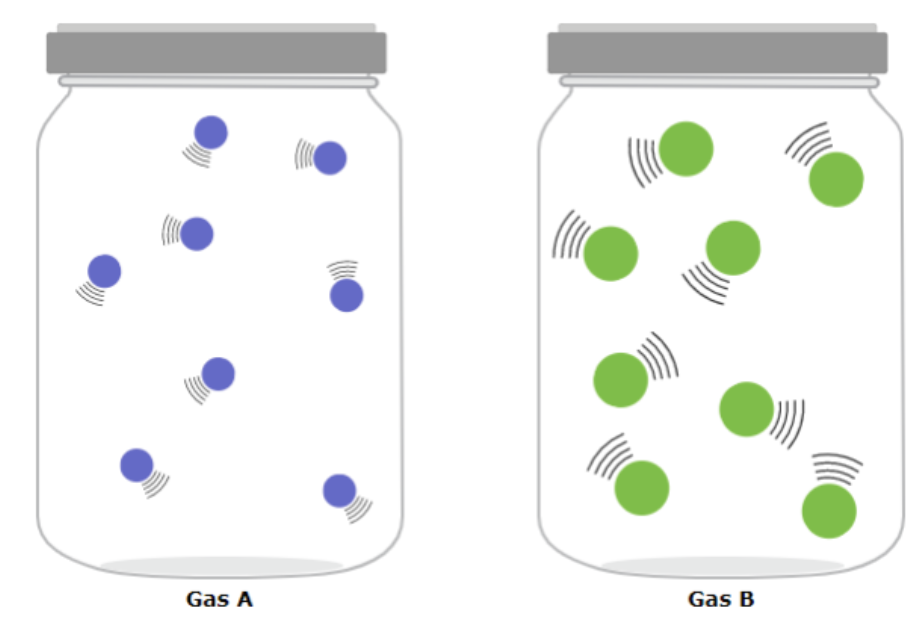
Is the kinetic energy of the two gases same or different and why or why not?

Different because velocity is the same but mass is different

The formula for calculating the kinetic energy is:

KE = 1⁄2 mv^2, where m is for mass (kg) and v is for velocity (meters/second), and KE is for kinetic energy (joules)

The ability to diffuse through a small hole

Rate of effusion

Rate of effusion is related to:

Size of particles

Graham’s Law describes relationship between:

Rate of effusion and size of particles

Graham’s law formula:

Rate 1 / Rate 2 = square root of (Molar mass 2 / Molar Mass 1)

As the particle size increases, the rate of effusion increases/decreases

Decreases

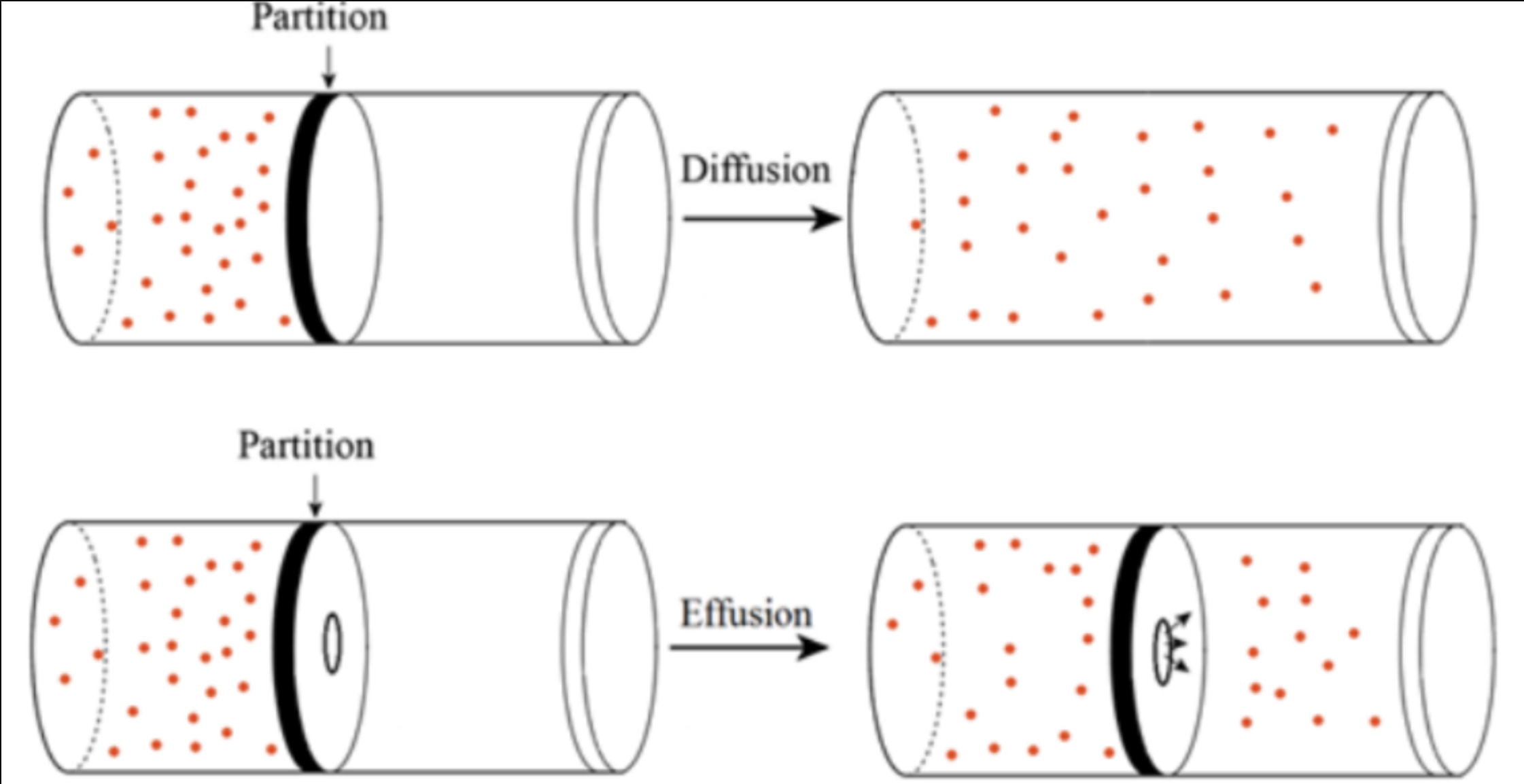
Draw diagrams to show differences between diffusion and effusion: