Lecture 10 & 11: Understanding Program Efficiency

Why we want to understand efficiency of programs

Constant Complexity

Logarithmic Complexity

Bisection Search

Bisection Search Complexity Analysis

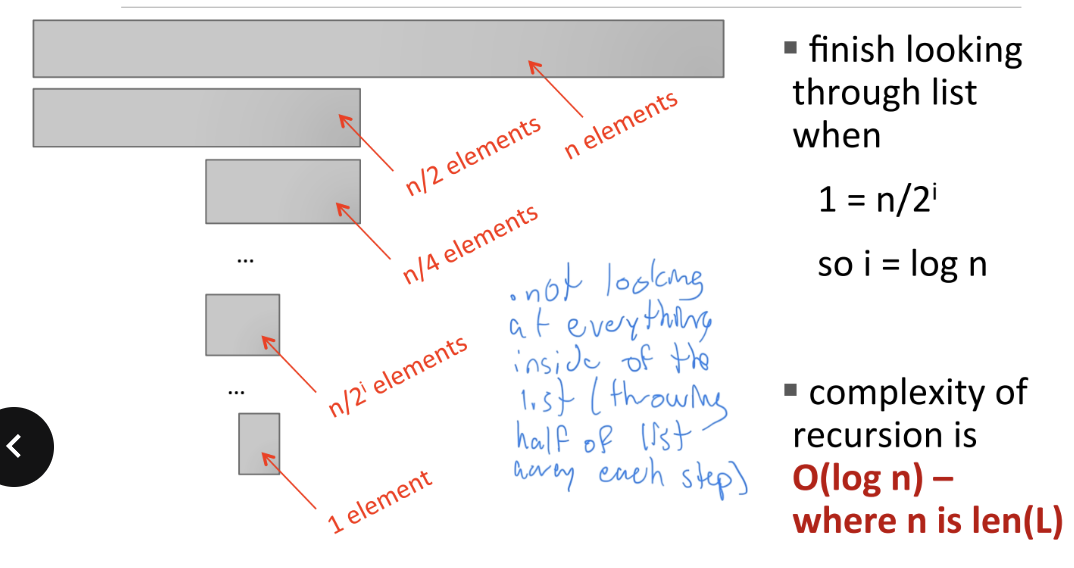
Complexity of First Bisection Search Method

Bisection Search Alternative

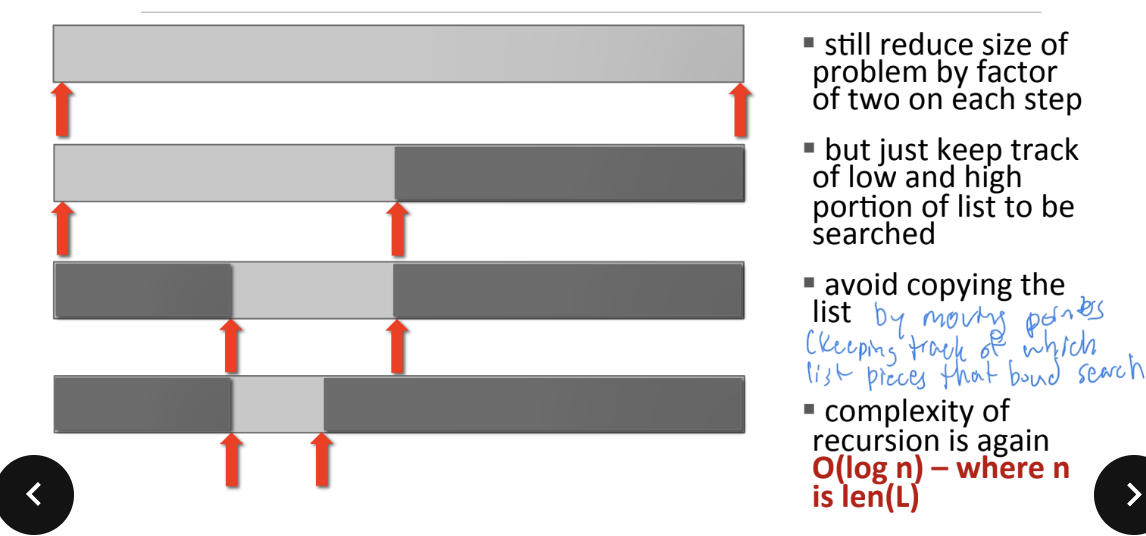
Complexity of 2nd Bisection Search Method

Linear Complexity

• searching a list in sequence to see if an element is present

• iterative loops

O() for Iterative factorial

O() for Recursive Factorial

Log-Linear Complexity

• many practical algorithms are this

• very commonly used algorithm of this complexity is merge sort

Polynomial Complexity

• most common algorithms of this complexity are quadratic, i.e, complexity grows with square of size of input

• commonly occurs when we have nested loops or recursive function calls

Exponential Complexity

• recursive functions where more than one recursive call for each size of problem (ex. Tower of Hanoi)

• many important problems are inherently this type of complexity (unfortunate but cost is high, will lead us to consider approximate solutions as may provide reasonable answer more quickly)

Power Set- Concept

Complexity of Power Set

Why does efficient programs matter?

Even though computers are getting faster, the size of problems/data sites are getting larger

Tradeoff between time and space efficiency of a program

• can someAmes pre-compute results are stored; then use “lookup” to

  retrieve (e.g., memoization for Fibonacci)

  ◦ will focus on Timme efficiency

Challenges in understanding efficiency of solution to a computational problem

• a program can be implemented in many different ways

• can solve a problem using only a handful of different algorithms

• would like to separate choices of implementation from choices of more abstract algorithm

How to evaluate efficiency of programs

• measure with a timer

• count the operations

• abstract the notion of growth (most appropriate)

Timing a Program

• use time module

• start clock

• call function

• stop clock

• time = difference between start clock time and stop clock time

Timing a Program is Inconsistent

Counting Operations

• assume that mathematical operations, comparisons, assignments, and accessing objects in memory are all steps that take constant time

• then count the number of operations executed as function of size of input

Why Counting Operations is better than Timing a Program

Goals of Order of Growth

• want to evaluate program’s efficiency when input is very big

• want to express the growth of program’s run time as input size grows

• want to put an upper bound on growth - as tight as possible

• do not need to be precise: “order of” not “exact” growth

• will look at largest factors in run time ( which section of the program will take the longest to run?)

• generally we want tight upper bound on growth, as function of size of input, in worst case

Big Oh Notation

measures an upper bound on the asymptotic growth (often called order of growth); used to describe worst case (occurs often and is the bottleneck when a program runs); express rate of growth of program relative to the input size; evaluate algorithm NOT machine or implementation

What does O(N) measure?

Interested in describing how amount of time needed grows as size of (input to) problem grows → given an expression for the number of operations needed to compute an algorithm, want to know asymptotic behavior as size of problem gets large → focus on term that grows most rapidly in a sum of terms & will ignore multiplicative constants (want to know how rapidly time required increases as increase size of input)

Analyzing Programs and Their Complexity

combine complexity classes by analyzing inside functions and apply some rules, focus on dominant term

Law of Addition for O()

• used with sequential statements

• O(f(n)) + O(g(n)) is O(f(n) + g(n))

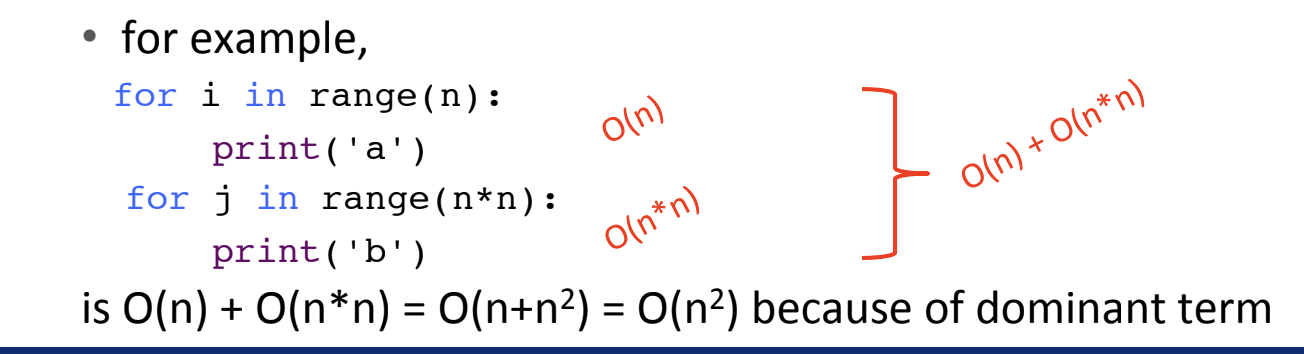
Law of Multiplication for O()

• used with nested statements/loops

• O (f(n)) * O(g(n)) is O(f(n) times g(n))

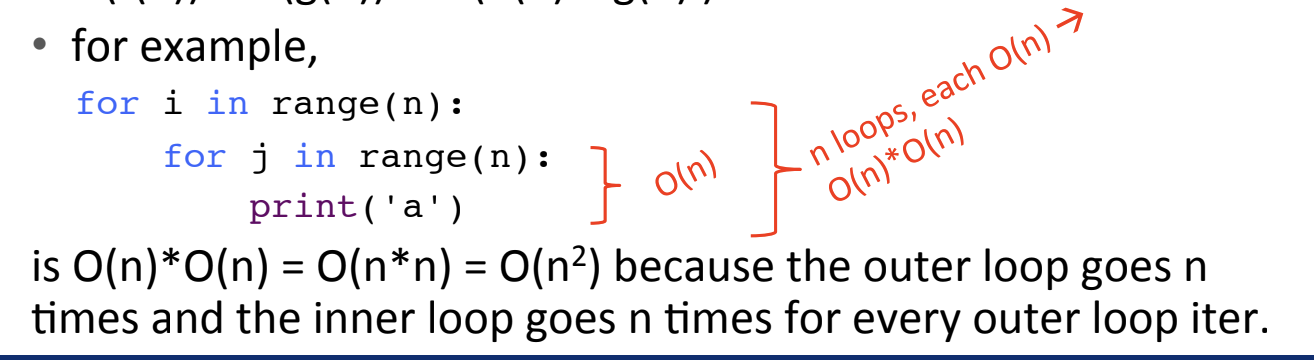
O(1)

denotes constant running time; code does not depend on size of problem

O (logn)

denotes logarithmic running time; reduce problem in half each time through process

O (n)

denotes linear running time; simple iterative or recursive programs

O (nlogn)

denotes log-linear running time

O(n^c)

denotes polynomial running time (c is a constant); nested loops or recursive calls

O (cⁿ)

denotes exponential running time ( c is a constant being raised to a power based on size of input); muliple recursive calls at each level

Complexity Ordered from Low to High

Linear Search on Unsorted List

Constant Time List Access

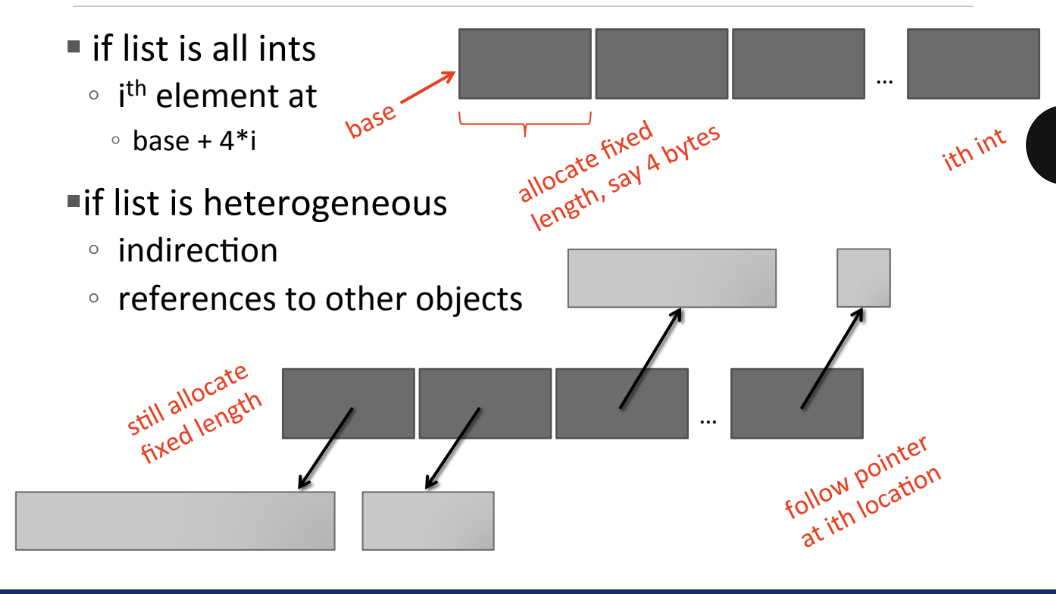
Linear Search on Sorted List

O() for Nested Loops

Big Oh Summary

Complexity of Common Python Functions: Lists (n is len(L))

Complexity of Common Python Functions: Dictionaries (n is len(d) (worst case)

Complexity of Common Python Functions: Dictionaries (n is len(d) (average case)