2.5 Continuity

Continuous Number

Definition l implicitly requires three things if f is continuous at a:

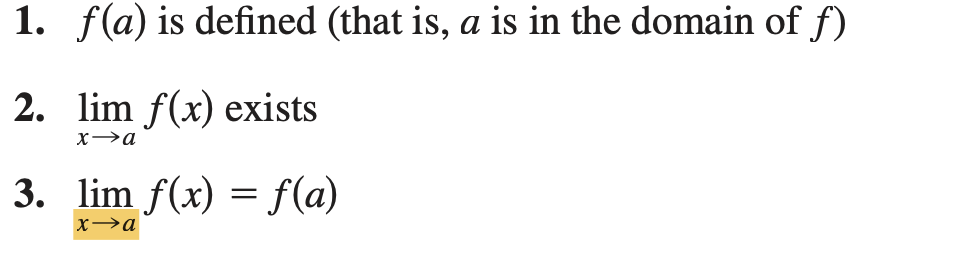
Discontinuity

If f is defined near a (in other words, f is defined on an open interval containing a, except perhaps at a), we say that f is discontinuous at a (or f has a discontinuity at a) if f is not continuous at a.

Continuity 

A function f is continuous from the right at a number a and continuous from the left at a if 

Continuous on an interval

A function f is continuous on an interval if it is continuous at

every number in the interval.

If f and g are continuous at a and c is a constant then the following

functions are also continuous at a:

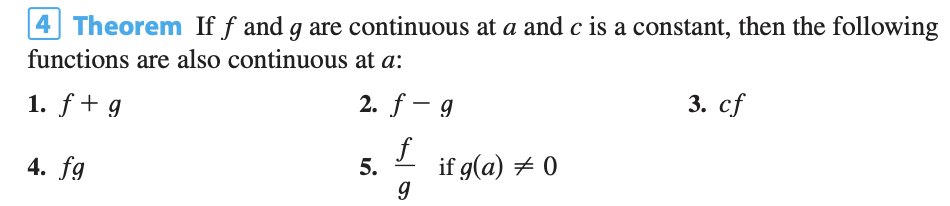
The following theorem was stated in Section 2.3 as the Direct Substitution Property.

The following types of functions are continuous at every number in

their domains:

polynomials, rational functions, root functions, trigonometric, functions, inverse trigonometric functions, exponential functions logarithmic functions

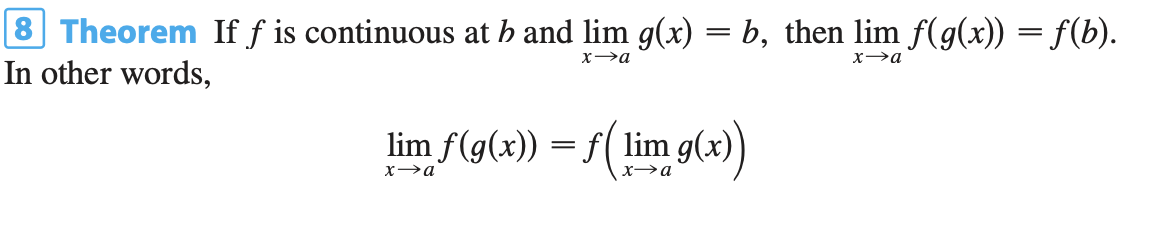
The Intermediate Value Theorem (IVT)

f is continuous on a closed interval [a,b]

N is any number between f(a) and f(b)

Then there exists at least one number c in the open interval (a,b)(a,b) such that f(c)=N.