Key Points : Electric and Magnetic Fields

All charged particles and surfaces produce an electric field around themselves. An electric field is a region where charged particles experience a non-contact force. Unlike gravitational fields, this force can be attractive or repulsive.

- Same charges repel each other

- Opposite charges attract each other

Electric field lines point in the direction that a positive charge would experience a force and so point from positive to negative

The force that acts between two charges is determined by Coulomb's Law. This states that:

- The force is directly proportional to product of the charges involved

- The force is inversely proportional to the square of the separation between the two charges.

As an equation, this is:

F = KQq/r²

where K = 1/4πε₀

If the force has a positive value, it is a repulsive force.

If the force has a negative value, it is an attractive force.

Electric field strength (E) is defined as the electrostatic force that a unit positive charge would experience, at a given point in the field. As an equation, this is:

E = F/Q

There are two further equations for finding the electric field strength, this first is for a radial field, while the second is for a field formed by parallel plates:

- E = KQ/r²

where K = 1/4πε₀

- E = V/d

The electric field strength around a point charge decreases as you move further away from it.

The weaker the electric field strength, the less dense the electric field lines are.

Electric Potential at a point is the amount of work done in moving a unit positive point charge from infinity to that point. As an equation this is:

- V = KQ/r

where K = 1/4πε₀

Electric potential difference is the work done moving a positive charge from one point to another.

This means that when you move a charge through a potential difference, work is done, equal to: ΔW = QΔV

As with gravitational fields, equipotentials are planes of points where the electric potential is the same, consequently no work is done when moving along these lines.

The capacitance (C) of a capacitor is the amount if charge it can store per unit of potential difference, measured in Farads.

C = Q/V

Capacitors consist of two metal plates separated by a dielectric. The capacitance of a given capacitor depends on the surface area of the plates, their separation and the dielectric being used.

C = Aε₀εr/d

A number of equations can be used to calculate the energy stored in a capacitor. The second and third equations are derived by substituting the capacitance equation into the first.

- E = ½QV

- E = ½CV²

- E = Q²/C

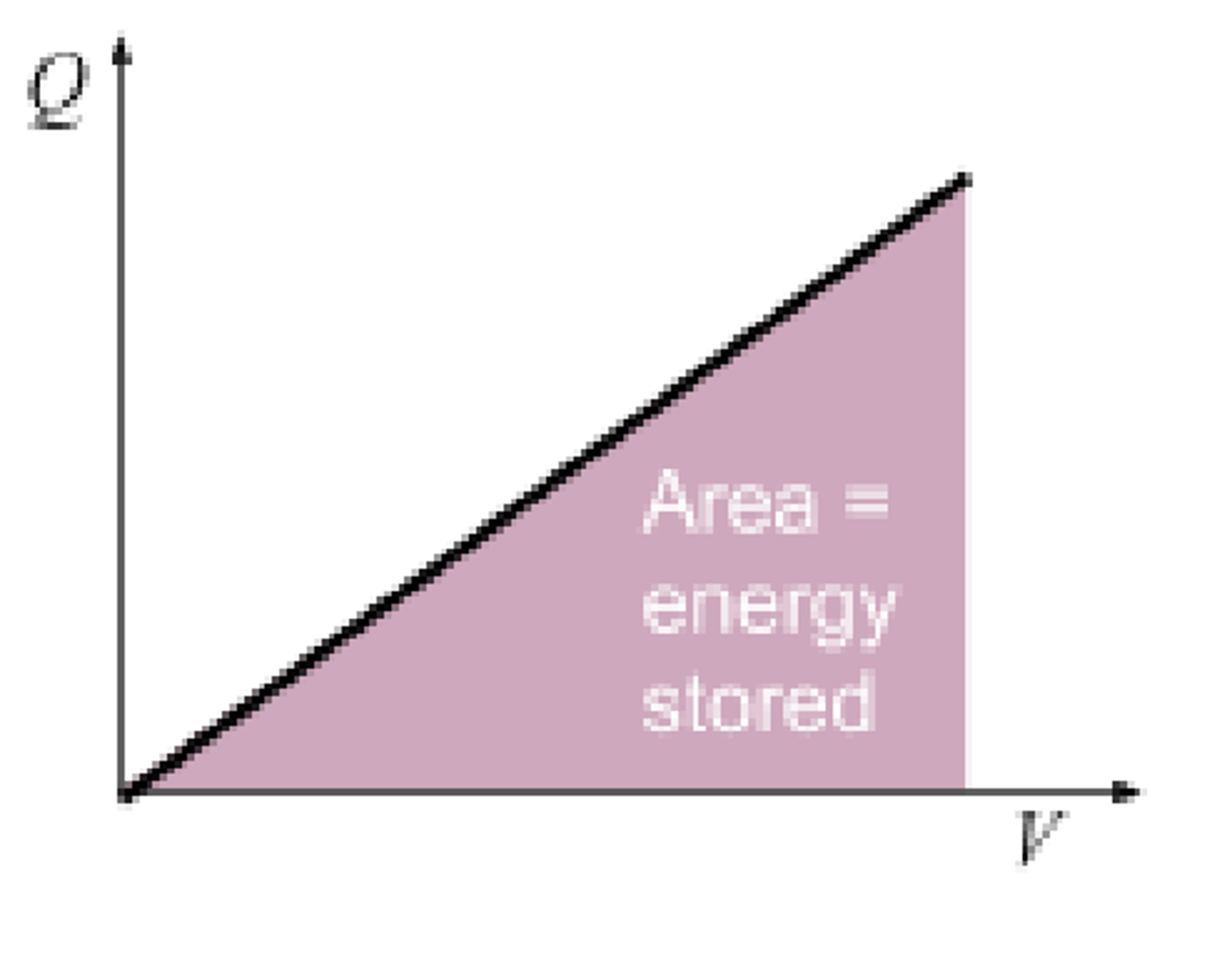
The energy stored can also be calculated by determined the area under a charge-voltage graph. The first energy stored equation above is derived from this fact.

The gradient of the graph is equal to the capacitance

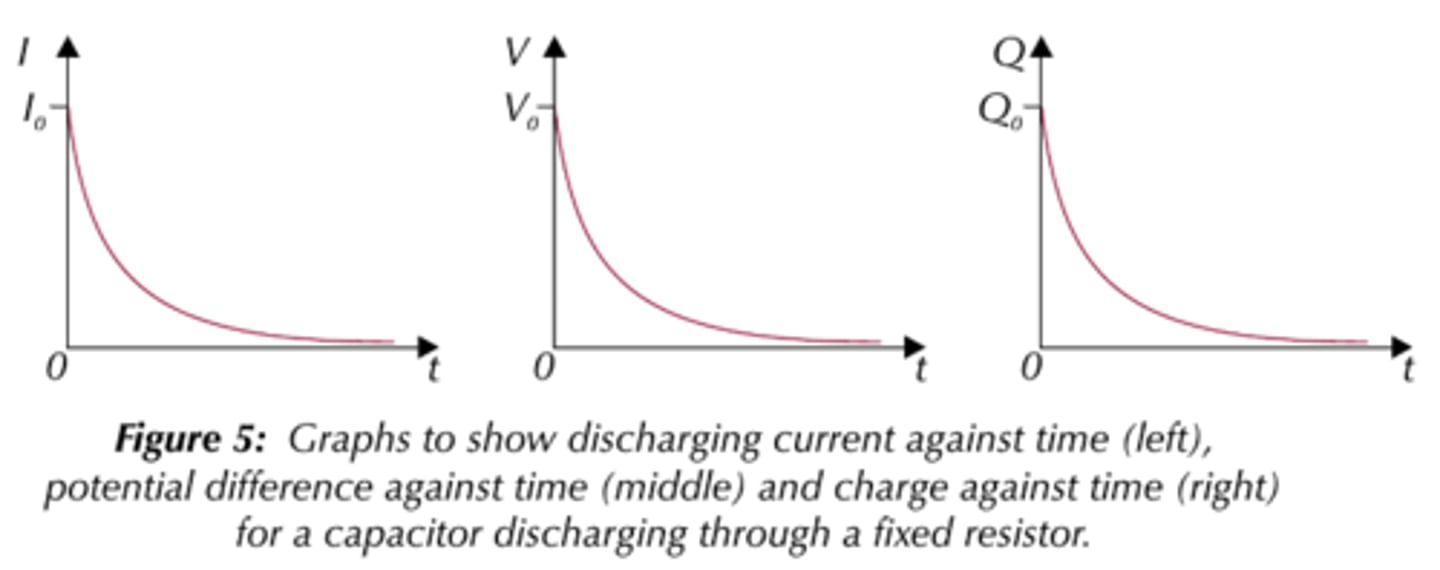
You should know the shapes of the charging and discharging graphs for a capacitor, for potential difference, charge and current.

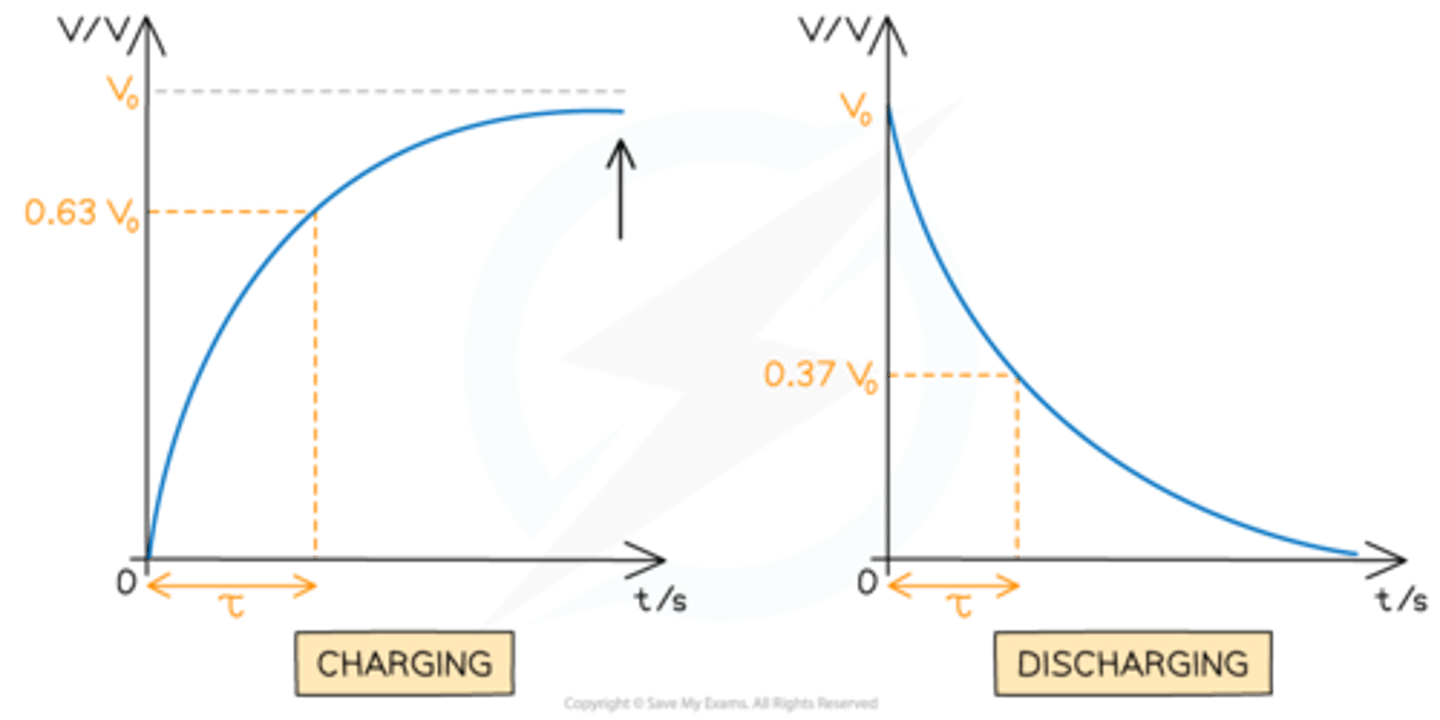
You should know the following formulas for the current, potential difference and charge of a discharging capacitor:

- I = I₀e⁻ᵗ/ᴿᶜ

- V = V₀e⁻ᵗ/ᴿᶜ

- Q = Q₀e⁻ᵗ/ᴿᶜ

You should also be able to derive the following equations by taking natural logarithms of both sides of the equations, and simplifying them using the log rules:

- ln I = lnI₀ - t/RC

- ln V = lnV₀ - t/RC

- ln Q = lnQ₀ - t/RC

An important value when working with capacitors is the time constant. It is equal to:

- The product of the resistance in the circuit and the capacitance of the capacitor

- The time taken to charge the capacitor to (1 - 1/e) of its final value.

- The time taken to discharge the capacitor to 1/e of its initial value.

When current passes through a wire, a magnetic field is induced around it. This field consists of concentric circles around the wire.

Magnetic flux density is a measure of the strength of a field and its unit is the Tesla

If a current carrying wire is placed in a magnetic field, the two fields interact and a force acts on the wire. The magnitude of this force depends on:

- The length of the wire

- The current passing through the wire

- The magnetic flux density of the field

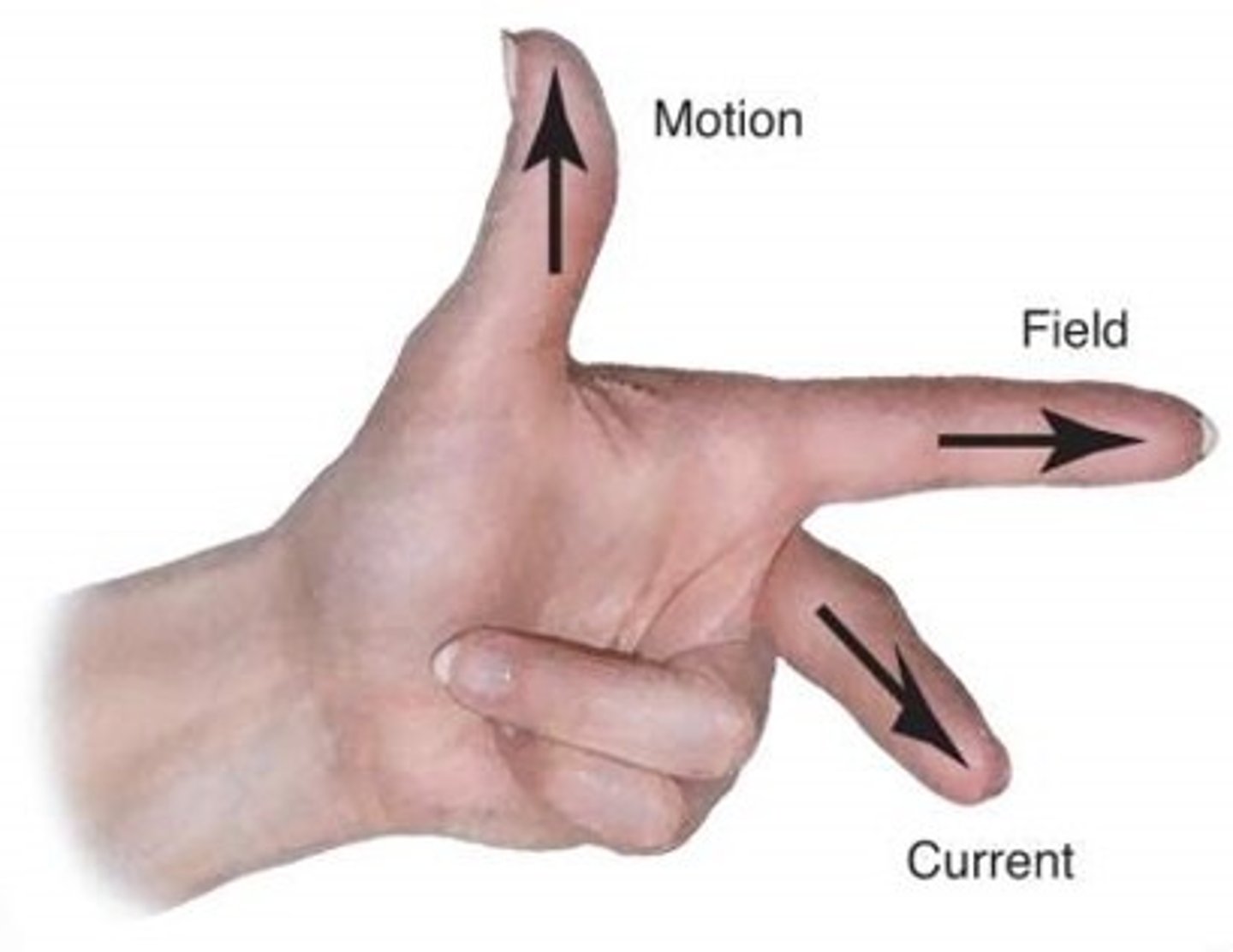
When a current-carrying wire experiences a force in a field, it is referred to as the motor effect. The magnitude of the force can be calculated using:

Force (N) = Magnetic Flux Density (T) x Current (A) x Length of Wire (m)

- F = BIL sinθ

The direction of the force (motion) can be determined using Fleming's Left Hand rule

When a charge moves in a magnetic field, it will experience a force. The magnitude of this force depends on:

- The magnitude of the charge

- The magnetic flux density of the field

- The velocity of the charge

The equation used to calculate the force is:

Force (N) = Magnetic Flux Density (T) x Charge (C) x Velocity (ms⁻¹)

F = BQv sinθ

Use Fleming's Left Hand Rule to determine the direction, with the second finger being the direction of a positive charge (so if its a negative charge, point it in the opposite direction)

Magnetic flux is a measure of the magnetic field that passes through a given area. It can be thought of as a measure of the number of field lines passing through the surface, or the density of the field line that are passing through it.

Magnetic Flux (Wb) = Magnetic Flux Density (T) x Area(m²)

ϕ = BA

This only applies when the magnetic field lines are perpendicular to the area.

If using a coil, a more useful quantity is magnetic flux linkage. This is the magnetic flux multiplied by the number of turns of the coil the field passes through.

Nϕ = B A N

If a current-carrying conductor moves relative to a magnetic field , an EMF is induced. This is as a result of the charge carriers in the conductor experiencing a force. If the conductor forms a complete loop, a current flows as a result of the induced EMF.

The law that governs the magnitude of the induced EMF is Faraday's Law which states that:

The magnitude of the induced EMF is directly proportional to the rate of change of magnetic flux linkage.

As an equation, this is:

- ε = N Δϕ/Δt

The direction of the induced EMF is governed by a second law known as Lenz's Law. This states that:

The direction of an induced current is such that is opposes the change that created it.

An example of this is a magnet falling through a non-magnetic metal tube.

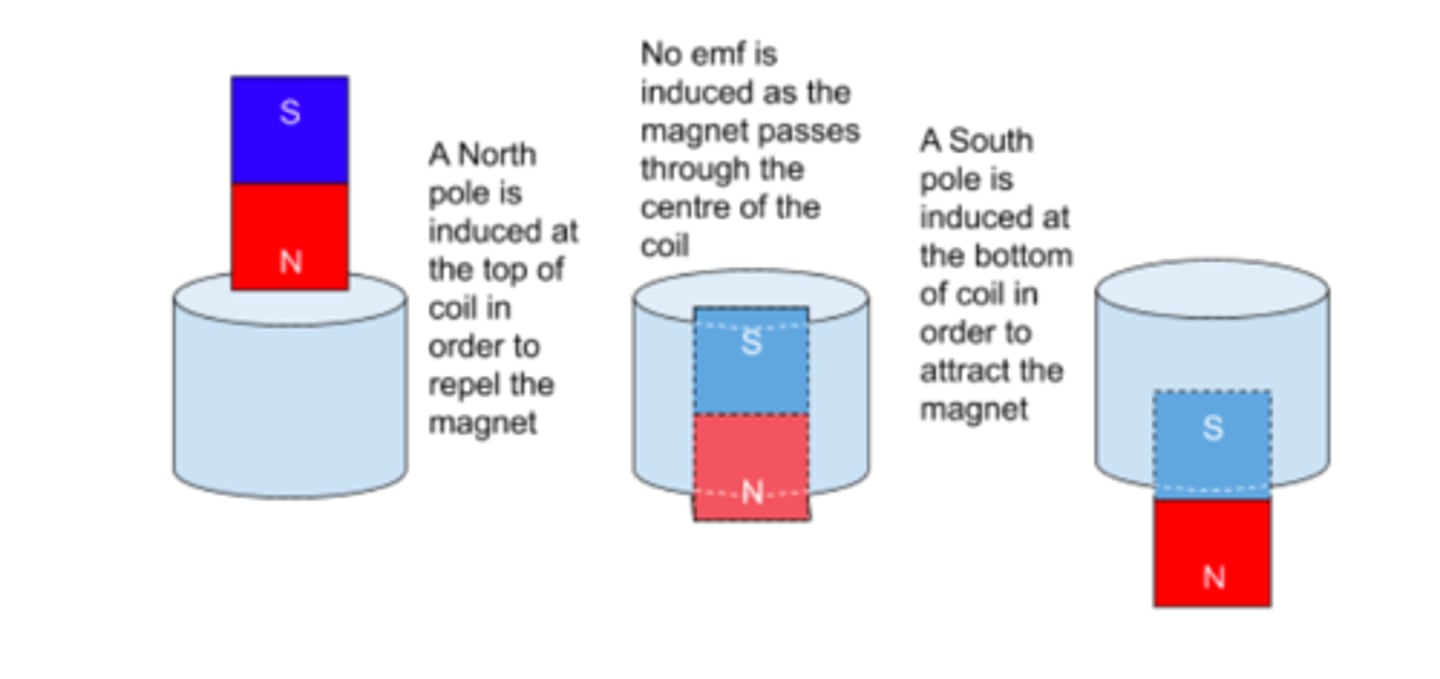
Faraday's and Lenz's laws can be combined in order to form the following equation for the value of emf generated:

ε = -d(Nϕ)/dt

This equation shows the magnitude of induced emf is equal to the rate of change of flux linkage, and that the emf is induced in the opposite direction to the change causing.

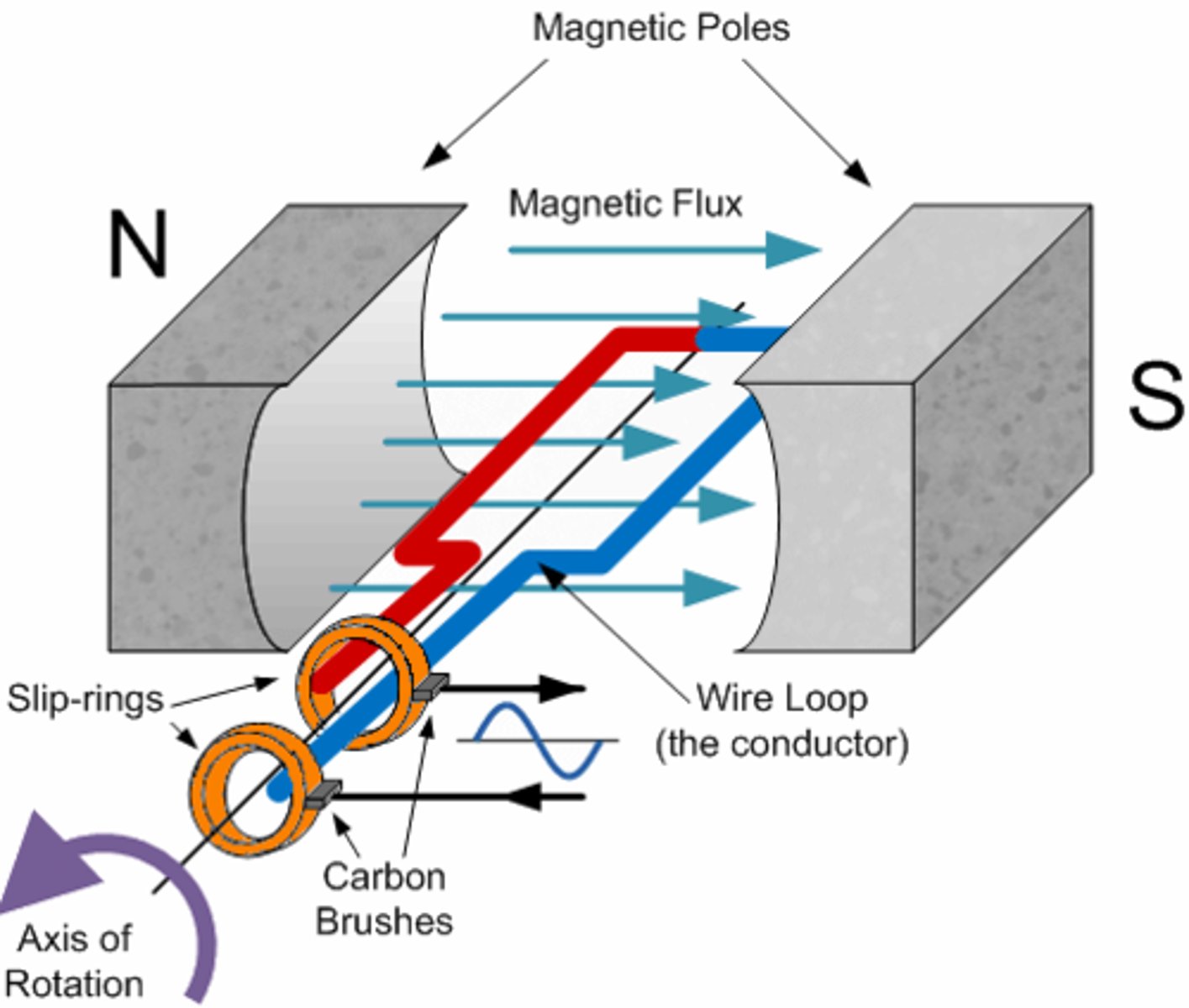
An A.C generator consists of a metal coil in a magnetic field. As the coil turns, the changing magnetic flux linkage passing through it induces an EMF.

The flux linkage varies sinusoidally between +BAN and -BAN.

- Nϕ = -BANcosωt

According to Faraday's law, the EMF is the rate of change of flux linkage.

- ε = ωBANsintωt

Increasing the speed/frequency of rotation or increasing the magnetic flux density will increase the maximum EMF.

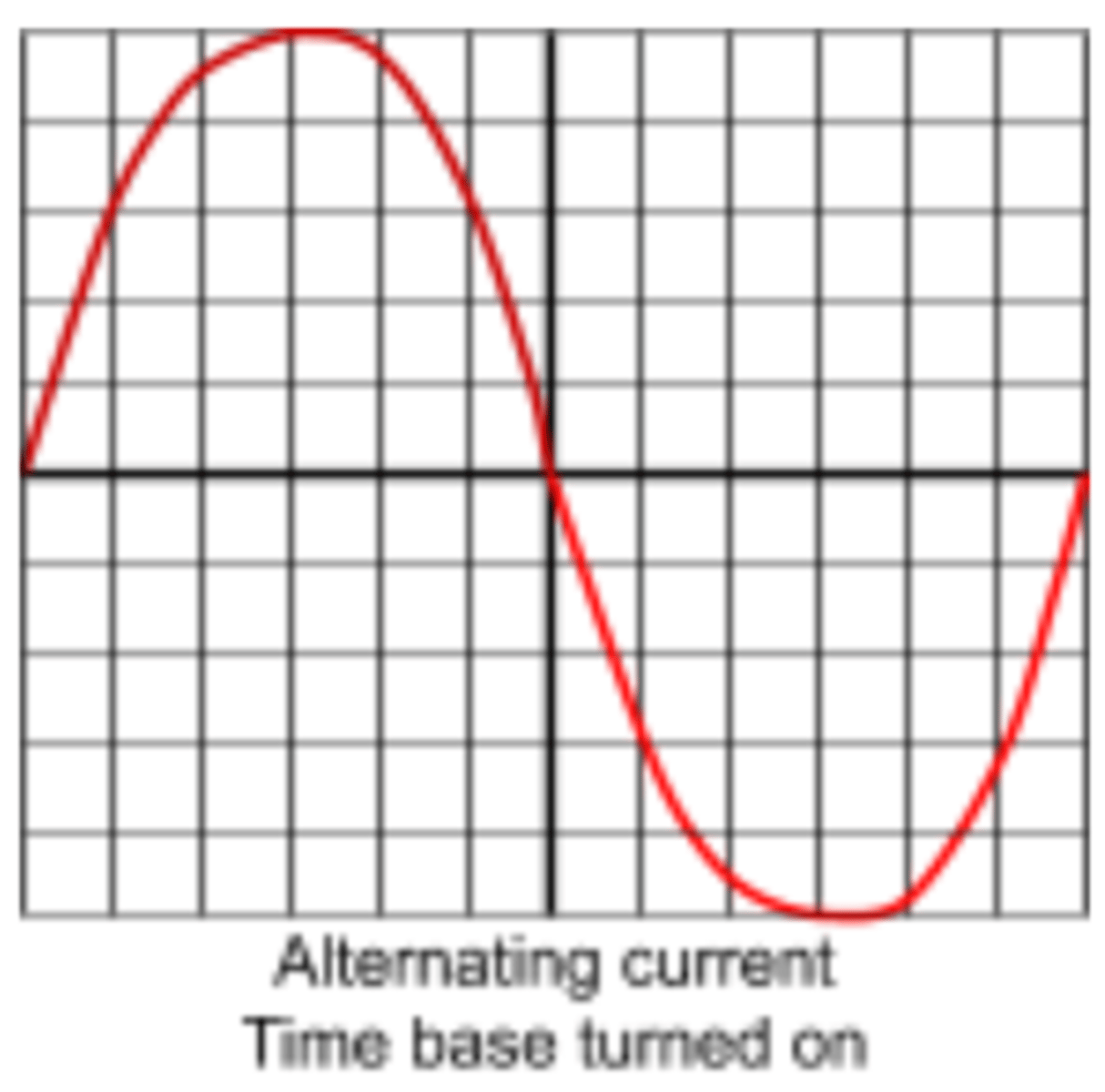
An oscilloscope is used to show voltage against time.

The time base controls how fast the wave moves across the screen (e.g. 2ms per division)

the Y-gain is the voltage per division (e.g. 2V per division.)

Vᵣ = V₀/√2

Iᵣ = I₀/√2

V₀ is the peak voltage. However the 'average voltage' is not the peak voltage, and therefore we find the root mean square (rms).

The rms value is usually quoted when referring to a AC power supply.

Powerᵣ = Iᵣ x Vᵣ

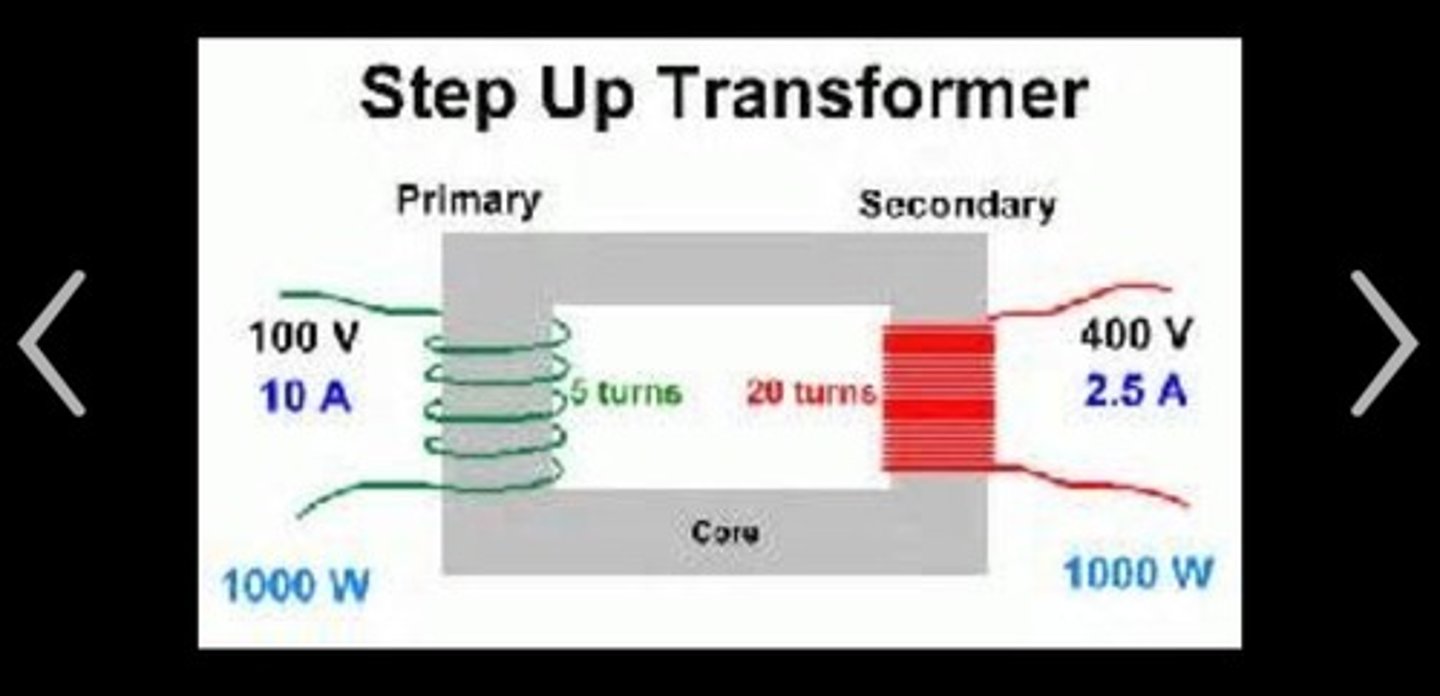
Transformers are used to increase or decrease the voltage of a power source. They come in two main types:

1. Step-Up: Number of coils on secondary coil > Number of coils on primary coil

2. Step-Down: Number of coils on primary coil > Number of coils on secondary coil

- A current passes through the primary coil which induces a magnetic field in the core.

- The current is an alternating-current so that the magnetic field in the core is constantly changng

- This constantly changing field causes a change of flux linkage in the secondary coil, which induces an EMF and therefore a current.

Inefficiencies:

If a transformer was 100% efficient, the power input would equal the power output - however power is lost due to:

- Eddy currents (looping currents which generate heat in the core)

- Heat loss in the wires

- Work done when magnetizing and demagnetizing the core

To reduce these factors:

- The core can be laminated to prevent eddy currents flowing

- The wires can be low resistance wires to reduce heating

- The core can be made from soft iron which is easily magnetized.