Machine Learning Review Questions Week 9

Which of the following is NOT a primary component of an artificial neuron?

c) Learning Rate

What is the primary function of the weights in an artificial neuron?

c) To determine the strength of input connections

The bias term in an artificial neuron primarily helps to:

b) Allow the neuron to activate even with zero inputs

What is the key purpose of the activation function in an artificial neuron?

c) To introduce non-linearity

If all inputs to a neuron are zero, which component ensures the neuron can still produce a non-zero output?

b) Bias

The three primary components of an artificial neuron are

weights, bias, and the output layer.

False (The third component is the activation function, not the output layer)

Weights in an artificial neuron are responsible for determining

the strength of the connection between inputs and the neuron.

True

The bias term forces the neuron to remain inactive when all inputs are zero.

False (It allows the neuron to activate even when all inputs are zero)

The activation function's primary role is to introduce linearity into the neuron's output.

False (Its primary role is to introduce non-linearity)

The activation function determines the neuron's output based on the weighted sum of inputs and the bias.

True

What is the MaxOut activation function?

MaxOut is an alternative to traditional activation functions, such as sigmoid, ReLU, and tanh.

𝑚𝑎𝑥𝑜𝑢𝑡(𝑥) = 𝑚𝑎𝑥(𝑧1, 𝑧2, . . . , 𝑧𝑘)

where zi = xi * Wi + bi, xi is the input, Wi is a weight matrix, and bi is a bias vector.

There are k sets of parameters, and k is a hyperparameter. For a neuron, k outputs are calculated with k sets of weights. Then, the maximum one is used as the neuron’s output.

What is the “dying ReLU” problem, and why does it occur?

The "dying ReLU" problem occurs when neurons get stuck, outputting zero for all inputs.

This happens when a large gradient pushes the neuron's weights such that it consistently receives negative inputs. Because the gradient of ReLU is zero for negative inputs, these neurons stop learning.

How does ReLU contribute to solving the vanishing gradient problem?

For positive inputs, ReLU has a constant gradient of 1. This helps prevent gradients from becoming extremely small during backpropagation, a common issue with sigmoid and tanh functions, especially in deep networks.

What types of neural network layers commonly use ReLU, and why?

ReLU is most widely used in the hidden layers of convolutional neural networks (CNNs) and other deep neural networks. Its efficiency and ability to mitigate the vanishing gradient problem make it well-suited for these architectures, where deep networks are necessary to learn complex patterns.

Why do we perform backpropagation during the test phase?

Backpropagation is only performed during training.

How do we initialize weights in a neural network?

Randomly

What happens if we initialize the weights to all zeros?

If the weights are initialized to zero, then all outputs will be zero regardless of the value of the inputs. Random initialization prevents us from getting stuck in a local minimum when performing cross-validation.

How do we optimize the weights in a neural network?

By backpropagation. Inputs are sent through the network in a feedforward manner.

Loss is the difference between the calculated output and the ground truth label.

Then, the gradient of the loss is back-propagated. Finally, weights are tuned based on the gradient of the loss.

What are the two major characteristics of an activation function?

It must be non-linear and differentiable.

What is a fully connected neural network?

Each neuron's output in the network is connected to the inputs of all neurons in the next layer.

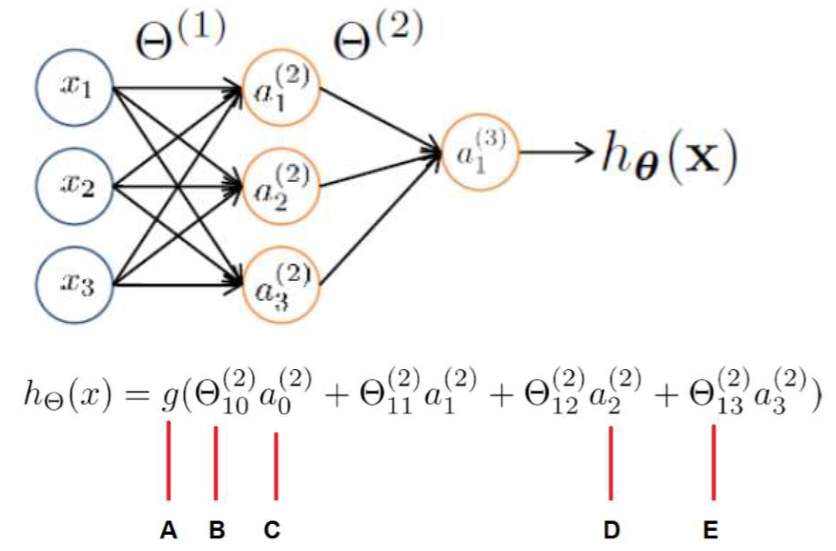
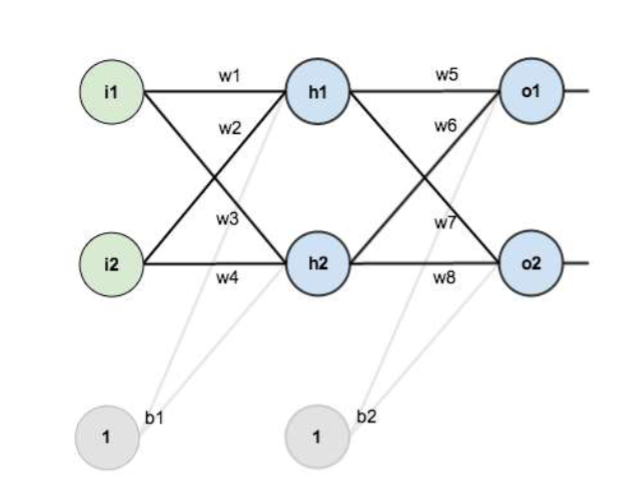
Consider the following MLP network.

What are the elements pointed out by letters A, B, C, D, and E?

A: The activation function of the output layer.

B: bias of the output layer

C: It is equal to 1

D: The output of the second neuron of the hidden layer (the second layer).

E: The coefficient of the link connecting the third neuron of layer two to the first neuron of the next layer.

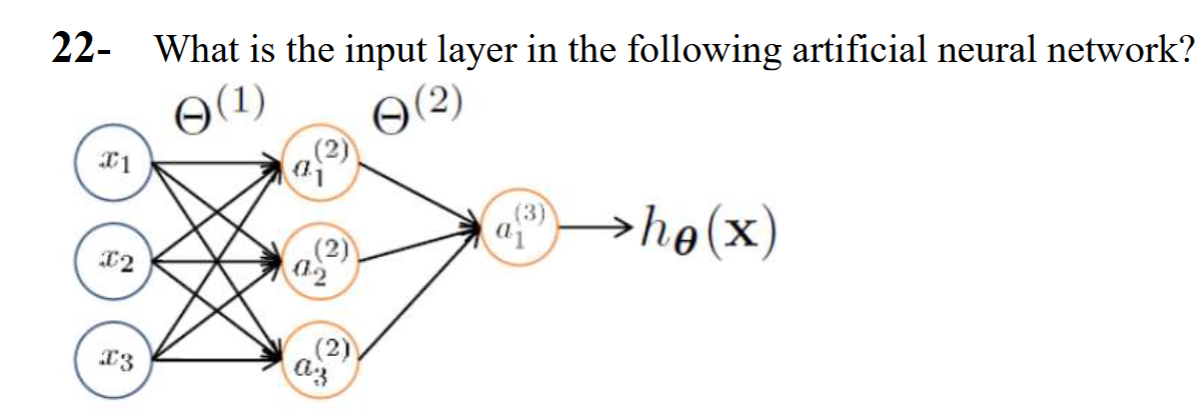
The input layer is not an actual layer. The input layer comprises the outside inputs (x1, x2, and x3) fed into the network. The first actual layer is the first hidden layer. In this diagram, there is one hidden layer and one output layer.

What is the main difference between classic machine learning and deep learning?

In the classic machine learning methods, features are manually extracted. In deep learning, the network learns to extract appropriate features.

What is an epoch?

One complete presentation of the training set to the network during training.

Consider the following code:

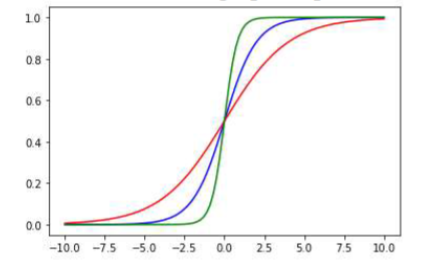
What will the three graphs represent? Which graph has the steepest slope?

They show sigmoid functions, which can be used as activation functions. The Green graph has the steepest slope, and the red curve has the shallowest slope.

What is the Perceptron convergence theorem?

If the data labels are linearly separable, the Perceptron learning algorithm will converge and halt after a finite number of iterations.

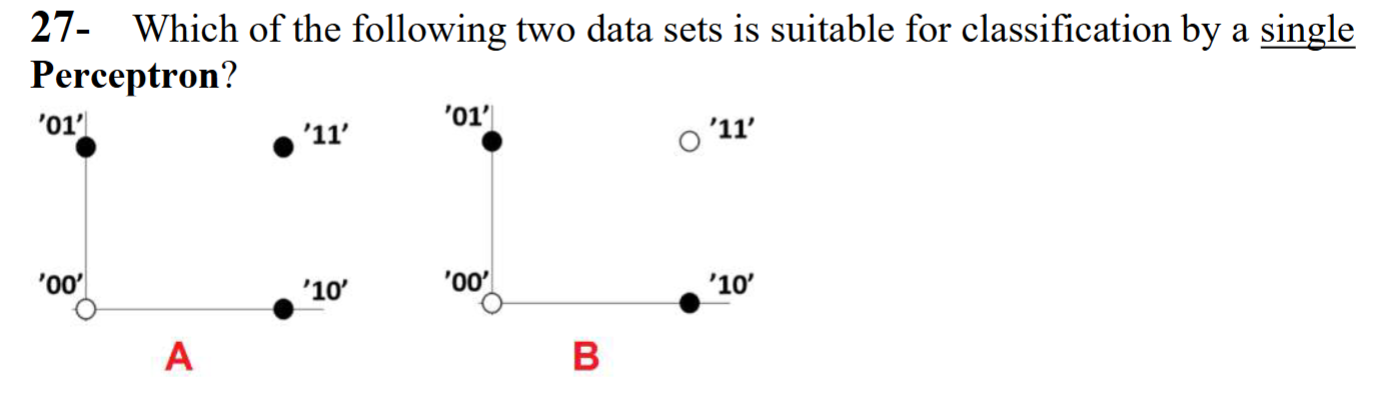
Set A is linearly separable and suitable for classification by a single Perceptron. But set B requires an MLP that can perform nonlinear classification.

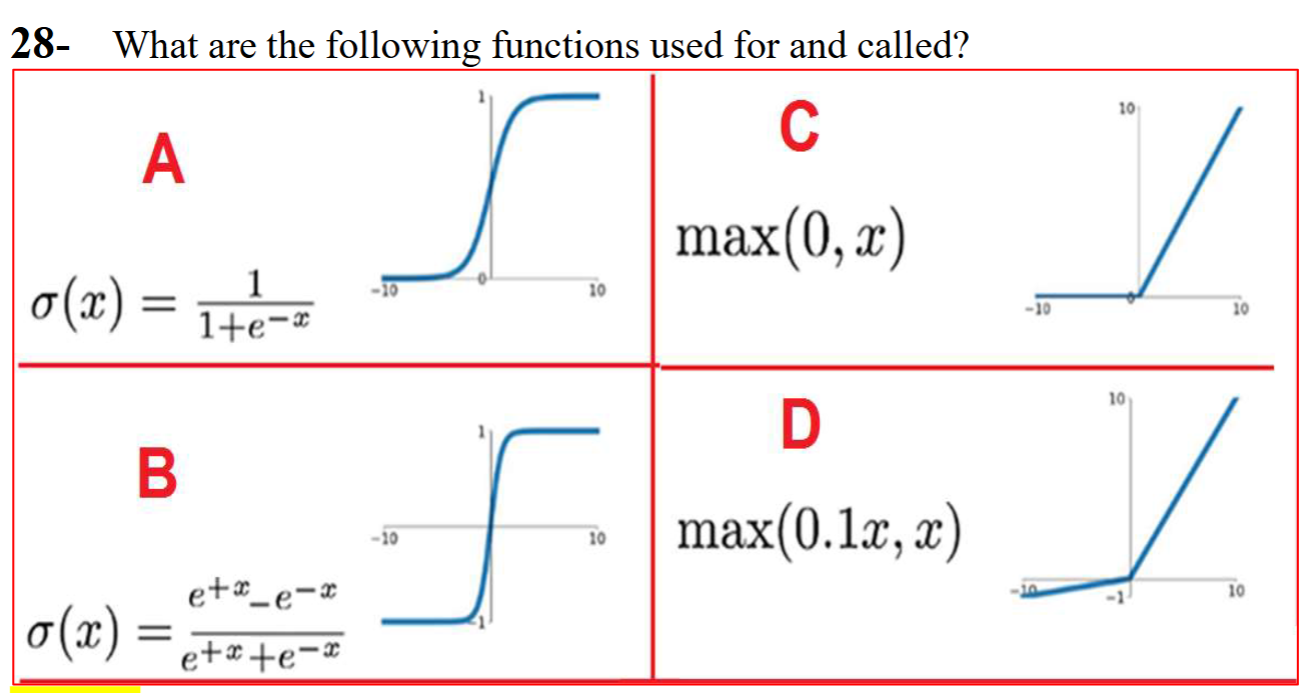
A is sigmoid,

B is tanh,

C is ReLu,

D is leaky ReLu.

What are the main advantages of the ReLu activation function?

1- ReLu causes representational sparsity. This means that any neuron that produces a negative output will be ignored. This accelerates the learning process since the weights of links connected to such neurons are not calculated.

2- ReLu prevents vanishing gradient. The gradient of the loss with respect to 𝑤_n will be proportional to the output loss, 𝑤_n, and the signal that is weighted by 𝑤_n.

Draw the shape of the ReLu function and its derivative.

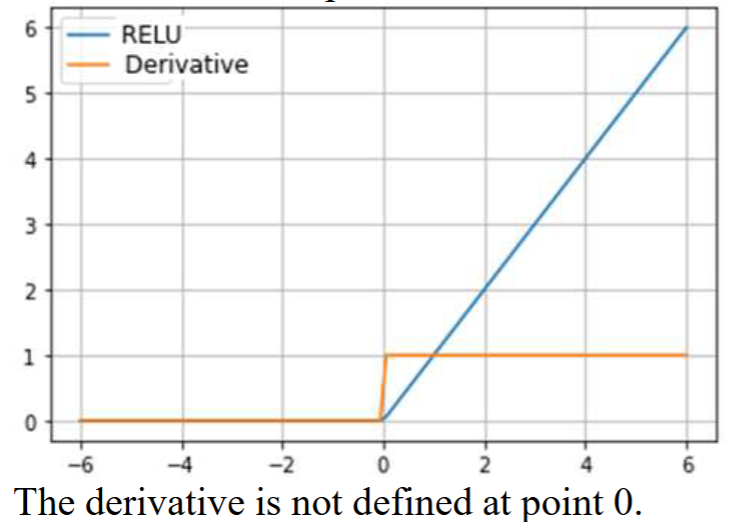
What is the vanishing gradient problem?

To update any network parameter, we need to calculate the gradient of the loss for that parameter. If the gradient is zero or close to that, the update process takes a long time or may even stop. Furthermore, as the number of layers grows, the possibility of a vanishing gradient increases. Sigmoid and tanh activation functions could cause a vanishing gradient. For example, the gradient of the sigmoid as a function of its input is:

డ௙(௫)

డ௫ = 𝑓(𝑥)(1 − 𝑓(𝑥)). This is a function of the output of the sigmoid. If the output of the sigmoid is small, the gradient becomes small. In contrast, the gradient of the ReLU function for positive inputs is always one, regardless of the cell's output value.

What happens if we replace ReLu with an identity function (𝑓(𝑥) = 𝑥)?

The network cannot approximate nonlinear functions. The network would essentially reduce to a linear regression model, as the network's output would be a linear function of the input.

What is the derivative of the sigmoid function?

Which of the following is a key advantage of the ReLU activation function over the sigmoid function in deep neural networks?

A) ReLU avoids the vanishing gradient problem in the positive range.

Why is nonlinearity a mandatory characteristic for activation functions in multi-layer neural networks?

B) To allow the network to learn complex, non-linear relationships in data.

Which of the following best describes the 'vanishing gradient' problem?

D) Gradients become extremely small, making it difficult for earlier layers to learn.

During backpropagation, how are the parameters (weights and biases) of a neural network adjusted?

A) Based on the difference between predicted and actual outputs, using gradient descent.

Which of the following is a common issue with the sigmoid activation function that ReLU helps to mitigate?

C) It suffers from the vanishing gradient problem due to its squashing effect.

The sigmoid activation function is commonly used in the output layer for binary classification problems because its output can be interpreted as a probability.

True

If a neural network uses only linear activation functions, it can

learn any complex, non-linear relationship in the data.

False

Backpropagation is primarily used to adjust the input features

of a neural network.

False

The vanishing gradient problem is more likely to occur in very deep neural networks that use activation functions like sigmoid or tanh.

True

ReLU (Rectified Linear Unit) is always preferred over sigmoid for all types of neural network layers, including output layers for binary classification.

False (Explanation: Although ReLU is popular for hidden layers, sigmoid remains a strong choice for binary classification output layers, as its probabilistic output range of 0 to 1 aligns well with the task of predicting likelihoods.)

Consider the following neural network. Assume that outputs O1 and O2 are outputs of sigmoid activation functions. Target1 and Target2 are the ground truth for the outputs O1 and O2. Mean Squared Error is our loss function. Calculate the derivative of the loss for w5.

Please note that the derivative is the slope of a line tangent to the cost function, so the steeper the slope, the more incorrect we are.

Here, we are using the sigmoid activation function for all neurons.

The derivative for w5 is a function of O1. The same will happen when we go back to h1 and h2. This could cause a vanishing gradient.

If the neuron's output is small, the gradient could become useless.

What is the defining characteristic of a Multilayer Perceptron (MLP)?

It includes at least one hidden layer between the input and output layers.

What is the purpose of backpropagation in training an MLP?

It calculates and propagates the error gradient through the network to update the weights.

What role does the chain rule play in backpropagation?

It enables the calculation of gradients for each layer by multiplying the partial derivatives of consecutive layers.

What is the "forward pass" or “forward propagation” in MLP training?

It refers to feeding input data through the network to generate an output.

What is the "backward propagation" in MLP training?

It involves calculating the error gradient and updating the weights based on that error.

A fully connected (dense) network with 11 inputs and two hidden layers with six neurons, each with ReLU activation functions. Additionally, one neuron is located in the output layer, utilizing the Sigmoid activation function. We perform mini-batch processing and train for 100 epochs. The output of the Sigmoid is converted to binary.

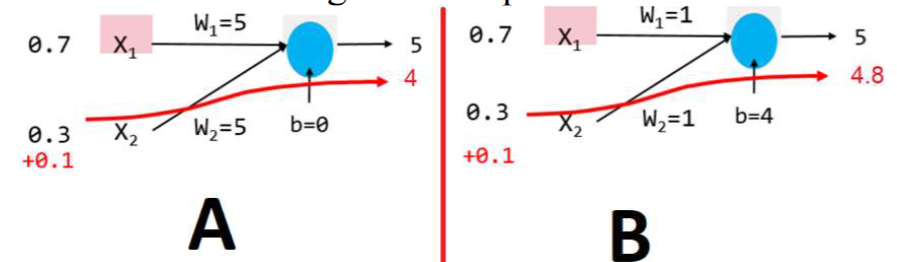
The following diagram illustrates that we tested one neuron with two different sets of weights and inputs.

The inputs of case A are first 0.7 and 0.3, which produce an output of 5. Then, the inputs are changed to 0.7 and 0.1, which produce an output of 4. This experiment demonstrates that A is ill-conditioned, while B is well-conditioned. Please explain why we want a neural network to be well-conditioned and how it is achieved.

In this experiment, A’s output significantly changed due to a slight input variation, making it ill-conditioned. This is due to its relatively large set of weights.

We aim to utilize regularization to constrain the parameters to be small and train a well-conditioned network. Such a network’s output will not fluctuate significantly for small changes in input.

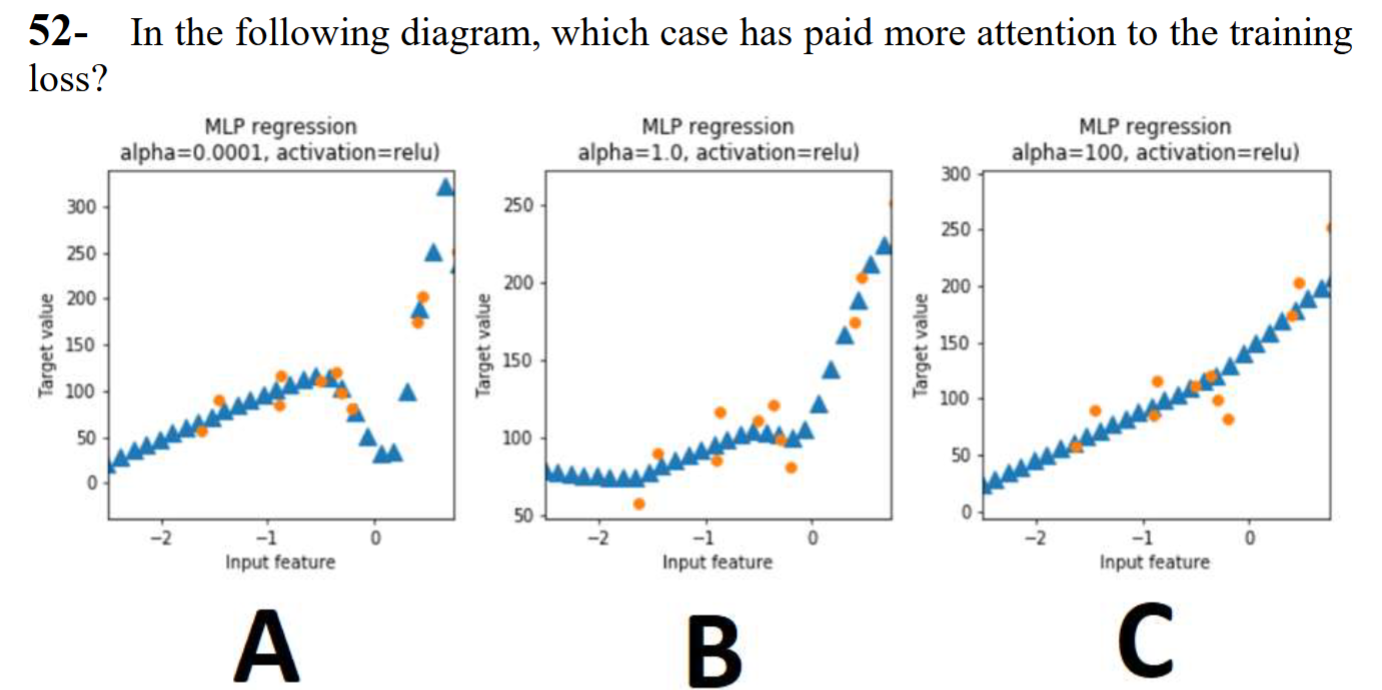
Case A has low regularization, meaning it places more value on the training loss. Hence, A is overfitted on the training data. C has a higher regularization factor and is not overfitted on the training data.

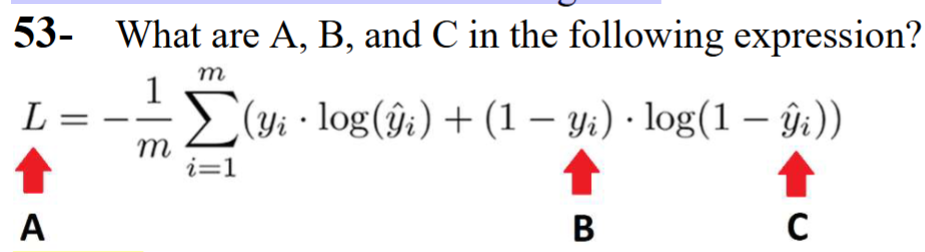
A is the cross-entropy loss function;

B is the actual label;

C is the probability of the label to be 1.

Regularization techniques in deep neural networks are primarily used to prevent overfitting.

True. Regularization methods such as L1, L2, and Dropout are specifically designed to reduce model complexity and prevent the model from performing too well on training data at the expense of generalization to unseen data (overfitting).

L1 regularization (Lasso) tends to drive some feature weights to exactly zero, performing feature selection.

True. L1 regularization adds a penalty proportional to the absolute value of the weights. This often results in sparsity, meaning some weights become exactly zero, effectively removing the influence of corresponding features.

Dropout regularization works by randomly setting a fraction of

input units to zero at each update during training.

True. Dropout temporarily 'drops out' (sets to zero) a random subset of neurons along with their connections during each training iteration, preventing complex co-adaptations and forcing the network to learn more robust features.

L2 regularization (Ridge) encourages smaller weights, helping to prevent complex models.

True. L2 regularization adds a penalty proportional to the square of the magnitude of weights. This encourages weights to be small but rarely exactly zero, thereby reducing the influence of individual features and making the model simpler.

Early stopping is a regularization technique that involves stopping the training process when the training loss begins to increase.

False. Early stopping monitors the validation loss (not training loss). Training is stopped when the validation loss starts to increase, indicating that the model is beginning to overfit the training data and generalize poorly to unseen data.