Mean Value Theorem and Rolle's Theorem

This set of flashcards covers key concepts related to the Mean Value Theorem and Rolle's Theorem, including definitions and interpretations of continuity, differentiability, and rates of change.

Mean Value Theorem (MVT)

States that if a function f is continuous on [a,b] and differentiable on (a,b), then there exists a number c in (a,b) such that f'(c) = (f(b) - f(a)) / (b - a).

Rolle's Theorem

States that if a function f is continuous on [a,b], differentiable on (a,b), and f(a) = f(b), then there exists a number c in (a,b) such that f'(c) = 0.

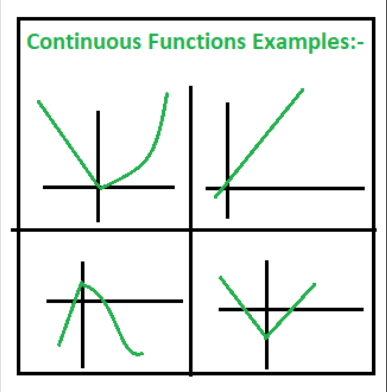
Continuous Function

A function is said to be continuous on an interval if its graph can be drawn without lifting the pencil from the paper.

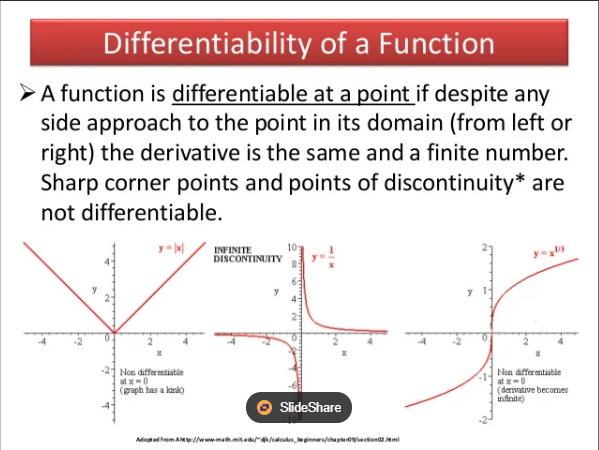
Differentiable Function

A function is differentiable at a point if it has a derivative at that point; the function must be continuous at that point.

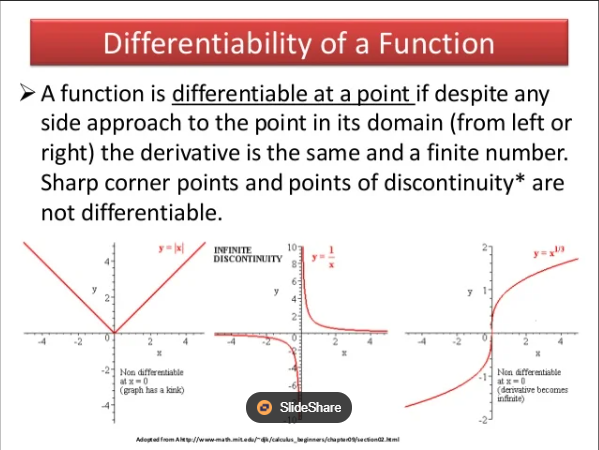
Instantaneous Rate of Change

The rate of change of a function at a particular point, represented by the derivative at that point.

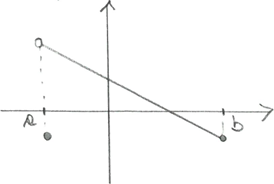
(MVT) What happens if we drop the assumption f(a) = f(b)

f is continuous on[a,b] and differentiable on (a,b), but there is no c in (a,b) where f’(c) = 0 

(MVT) What happens if we drop the assumption that f is differentiable on (a,b)?

f is continuous on [a,b] and f(a) = f(b), but there is no c in (a,b) where f’(c) = 0

(MVT) What happens if we drop the assumption that f is continuous on [a,b]?

f is differentiable on (a,b) and f(a) = f(b), but there is no c in (a,b) where f’(c) = 0

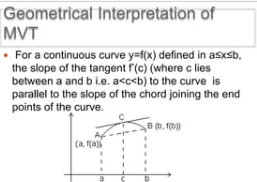
Geometric Interpretation of MVT

If the graph of f has no jumps (continuous) and is smooth (differentiable), then there is at least one number c in (a,b) so that the slope of the tangent line at c equals the slope of the line through endpoints (a, f(a)) and (b, f(b)): f’(c) = f(b)-f(a)/b-a

(MVT) Rates of Change Interpretation

The rate of change of a function over an interval [a, b], calculated as (f(b) - f(a)) / (b - a).

In Conclusion the MVT…

The MVT tells us that there’s a point c between a and b, where the instantaneous rate of change at c equals the average rate of change of f between a and b.

Corollary of Mean Value Theorem

If f'(x) = g'(x) for all x in some interval, then there exists a constant c such that g(x) = f(x) + c for all x in that interval.

Derivative

The derivative of a function gives the slope of the tangent line to the graph of the function at a given point.

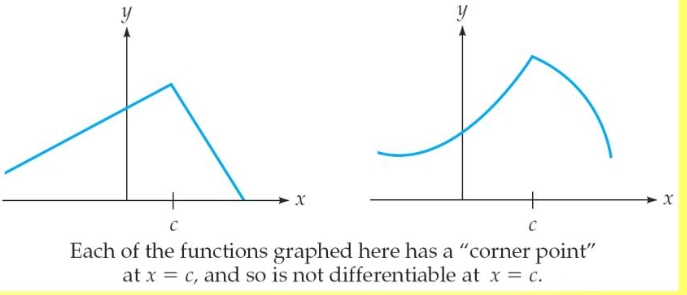
Corner Point

A point at which a function is not differentiable but still continuous; often exhibits a sharp change in direction.

Why is the MVT So Important?

The MVT is so important because it is the main theorem in Calculus! It helps us relate statements about f’ to statements about f in a direct way.

How does MVT impact limits and derivatives?

The definition of the derivative is f’(a) = lim(b→a) f(b)-f(a)/b-a, but the MVT tells us that under its assumptions, there is a number c in (a,b) where we can “drop the limit” and relate information about f’ directly to information about f. This results in its geometric interpretation.