Maths
1/13
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
14 Terms
Quadratic Formula of form ax2 + bx + c = 0
x = (-b +- √(b2 - 4ac))/2a
First Derivative
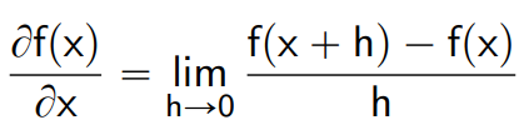
Arithmetic Growth Rate
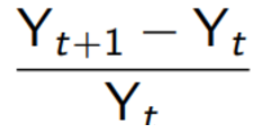
Logarithmic Growth Rate
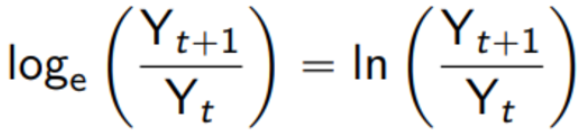
Locating Minima and Maxima of a Function

Stationary Points
Minima and maxima are what we call stationary points i.e., points of a function with a first derivative equal to zero z is a stationary point of f(x) if and only if:
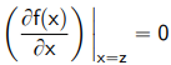
Inflection Points
a point where a function’s curvature shifts or, in mathematical terms, when a function’s second derivative equals zero z is an inflection point of f(x) if and only if:
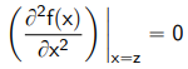
Global vs Local Optima
A function f(x) can have multiple minima and maxima
global minimum (maximum) – smallest (greatest) value of f(x) importantly, in all its domain (global -> for all xs)
local minimum (maximum) – smallest (greatest) value of f(x) in an interval of its domain (local -> for a subset of xs only)
Natural Logarithm Rule
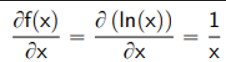
Rule on Exponentials of Base e
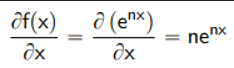
Partial Derivatives

Cross-Partial Derivatives

Second Order Partial Derivatives

Optimising Multivariate Functions
