Calc. 1( Limit of a Function and Intro Derivatives ( Tangent+ Velocity Problem
5.0(1)
5.0(1)
Card Sorting
1/24
Earn XP
Description and Tags
Goes through what a limit of a function is and is not , how to ind the slope of a tangent line, and a derivate at a point, and finding its function
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No study sessions yet.
25 Terms
1
New cards
What is the Difference Quotation Formula?
f(x+h)-f(x)/h
2
New cards
Common Behaviors Associated with Nonexistence of a Limit
1. f(x) approaches a different number from the right side of a than it approaches from the left side.
2. f(x) increases or decreases without bound as x approaches a.
3. f(x) oscillates between two fixed values as x approaches a.
3
New cards
Formula #1: Slope of the tangent line (Common Point)
Lim x➡️a f(x)-f(a)/x-a
4
New cards
Formula #2: Slope of Tangent Line+ Derivative at a Point( instantaneous rate of change at x=a
Lim h➡️0 f(a+h)-f(a)/h
5
New cards
Formula #3: Derivative Funiction( find a f(x) function
Lim h➡️0 f(x+h)-f(x)/h
6
New cards
Existence of a Limit Theorem
The limit of the right and left are the same value so the limit is same value.
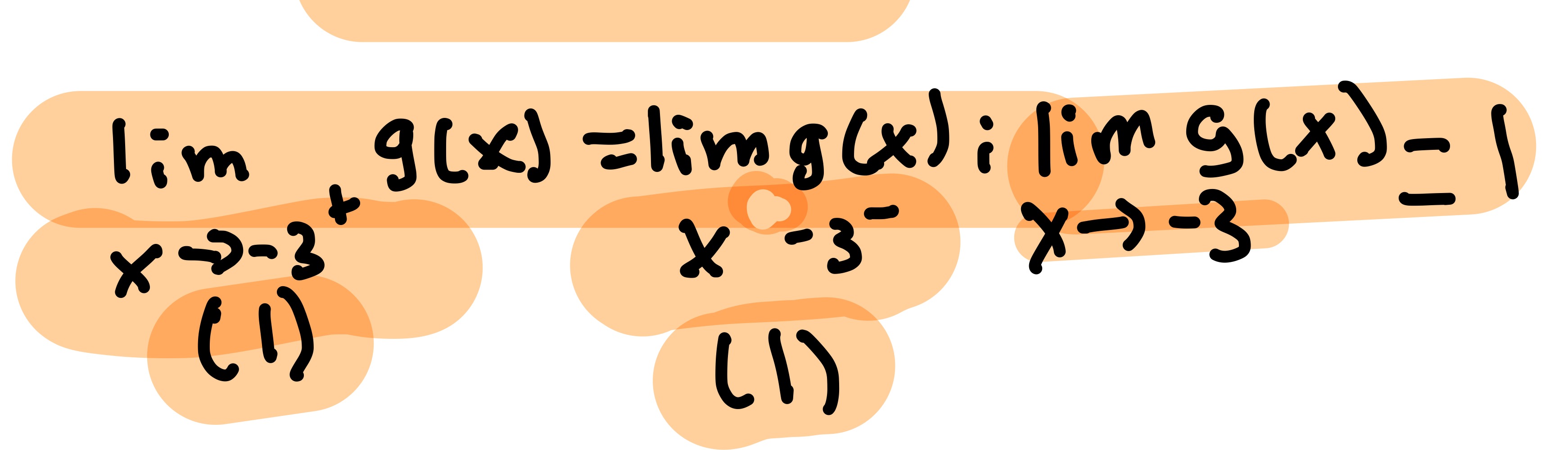
7
New cards
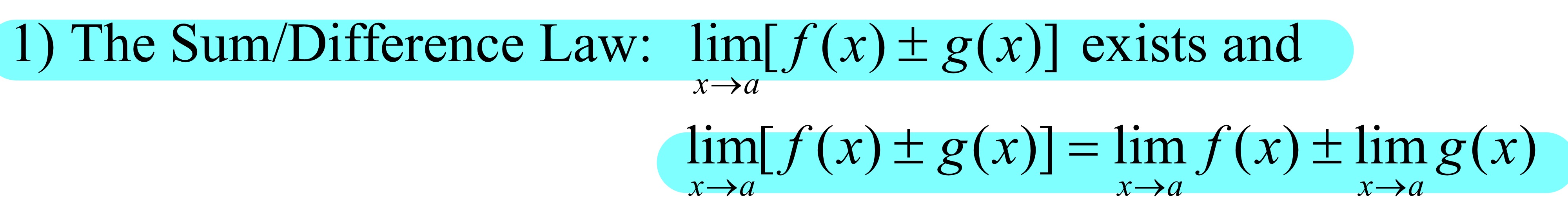
Basic Limit Laws#1: The Sum/Difference Law
You can distribute your limit to each part of the expression( put the limit before each factor)
8
New cards
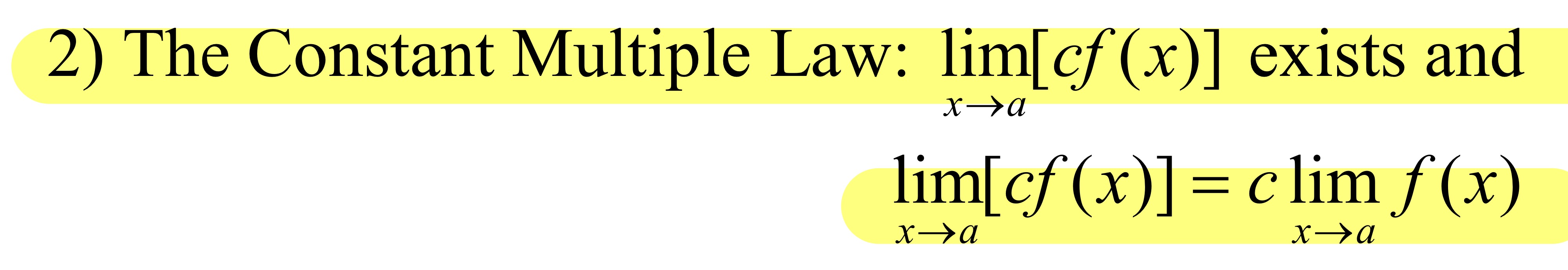
Basic Limit Laws#2: The Constant Multiple Law
The constant can be moved outside the limit and away from sitting next to the limit.
9
New cards
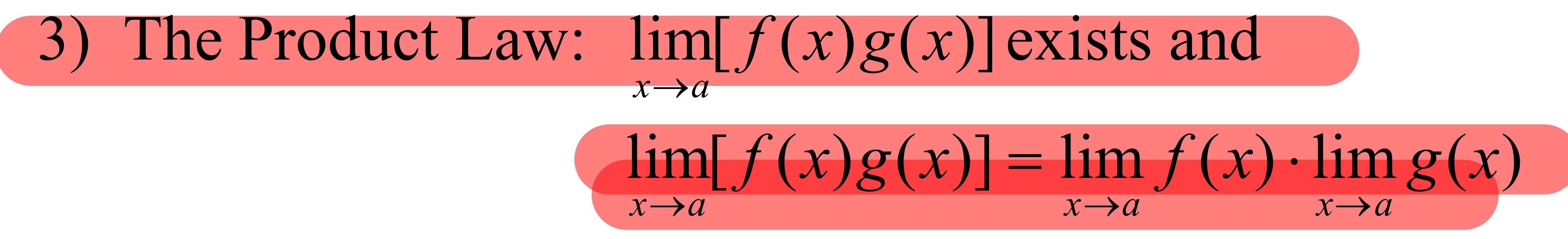
Basic Limit Laws#3: The Product Law
You can multiply each function by each other as long as they have the same limit
10
New cards
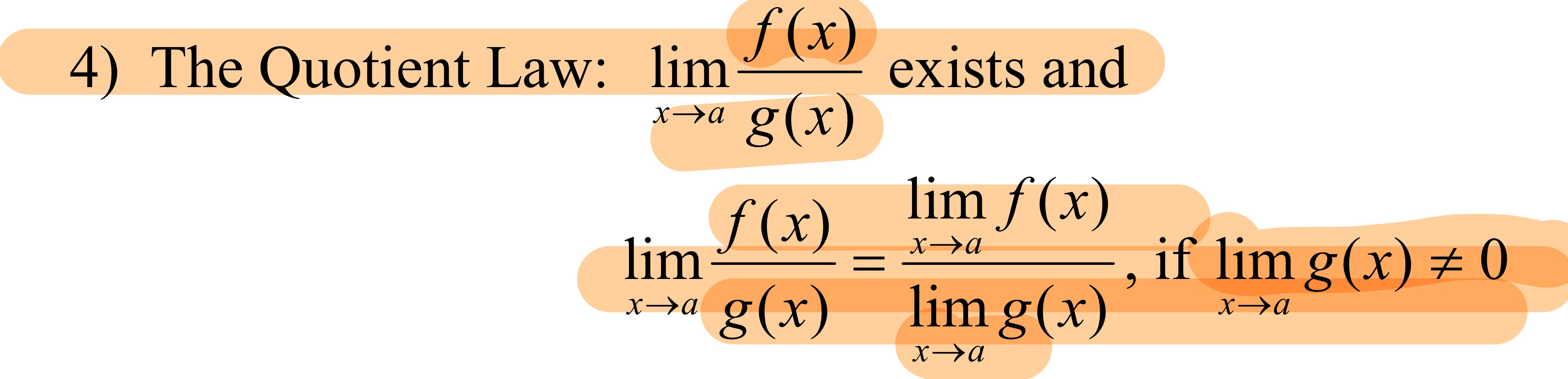
Basic Limit Laws#4: The Quotient Law
The value of the limit on num. and the limit of the denom. Equals the limit of the fun in num/ denom. As long as the denom. Does not equal zero.
11
New cards
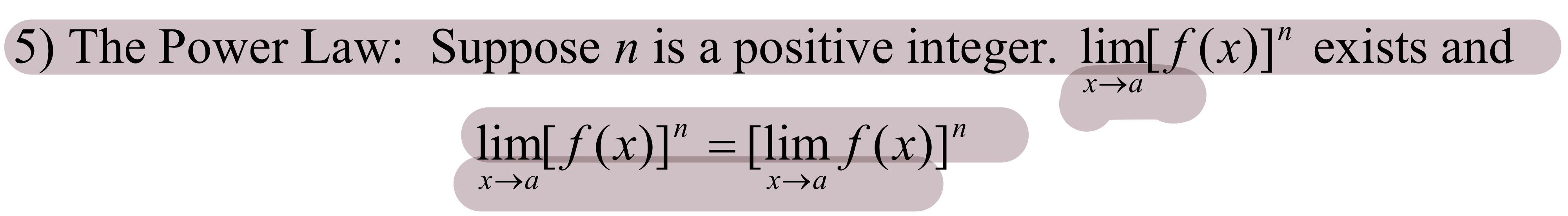
Basic Limit Laws#5: The Power Law
As long as the n(interfere) is positive than the limit can be moved ext to then function and done together
12
New cards

Squeeze Theorem:
If the upper function( right) and lower function(left) are equal and the function is between the other two , than that middle function equals the equaled value of the outside functions
13
New cards
Definition of Continuous

14
New cards
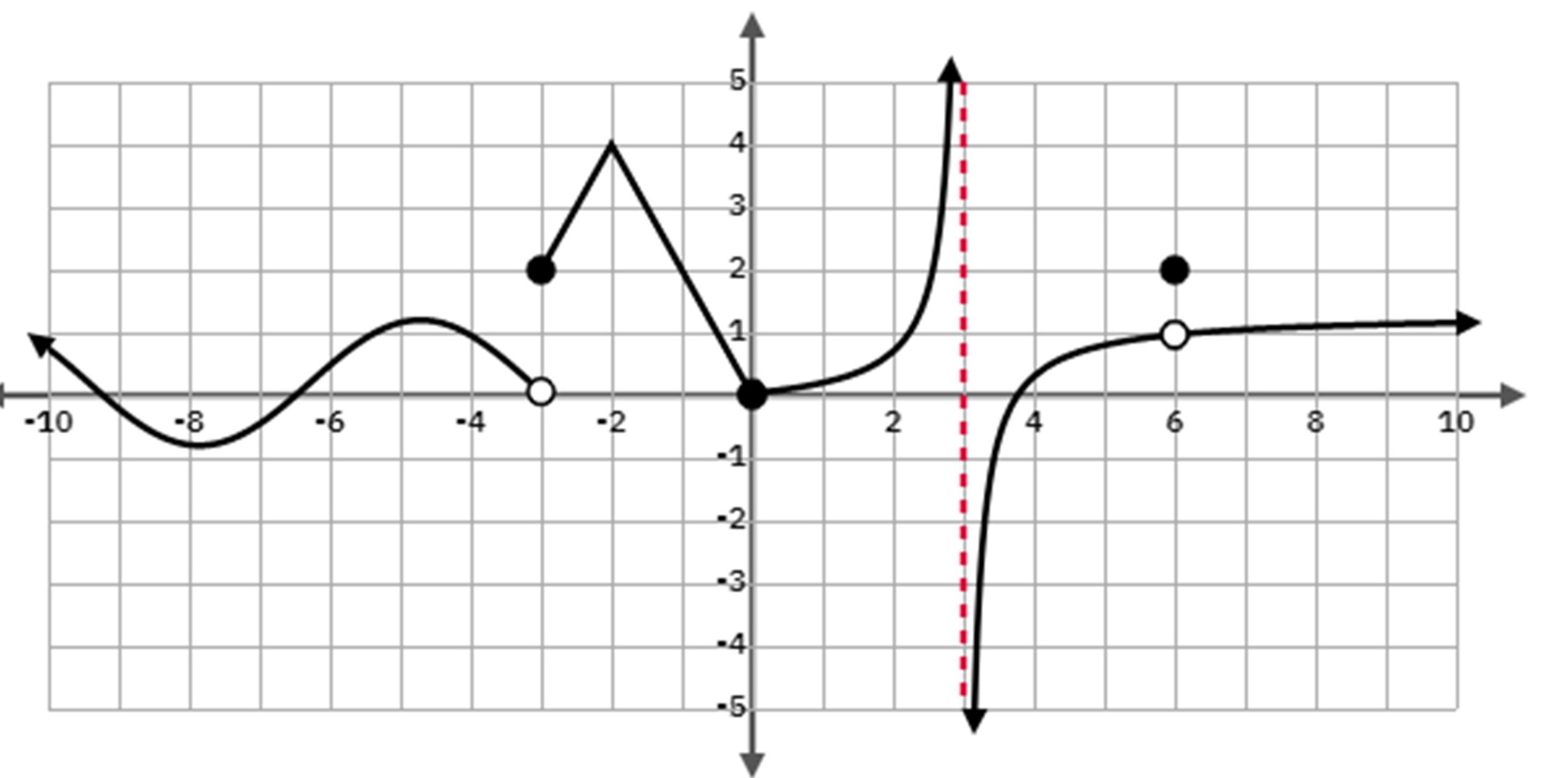
Discontinuity: Removable
If you can fill in the circle and create a continuous function( has a function value and limit)
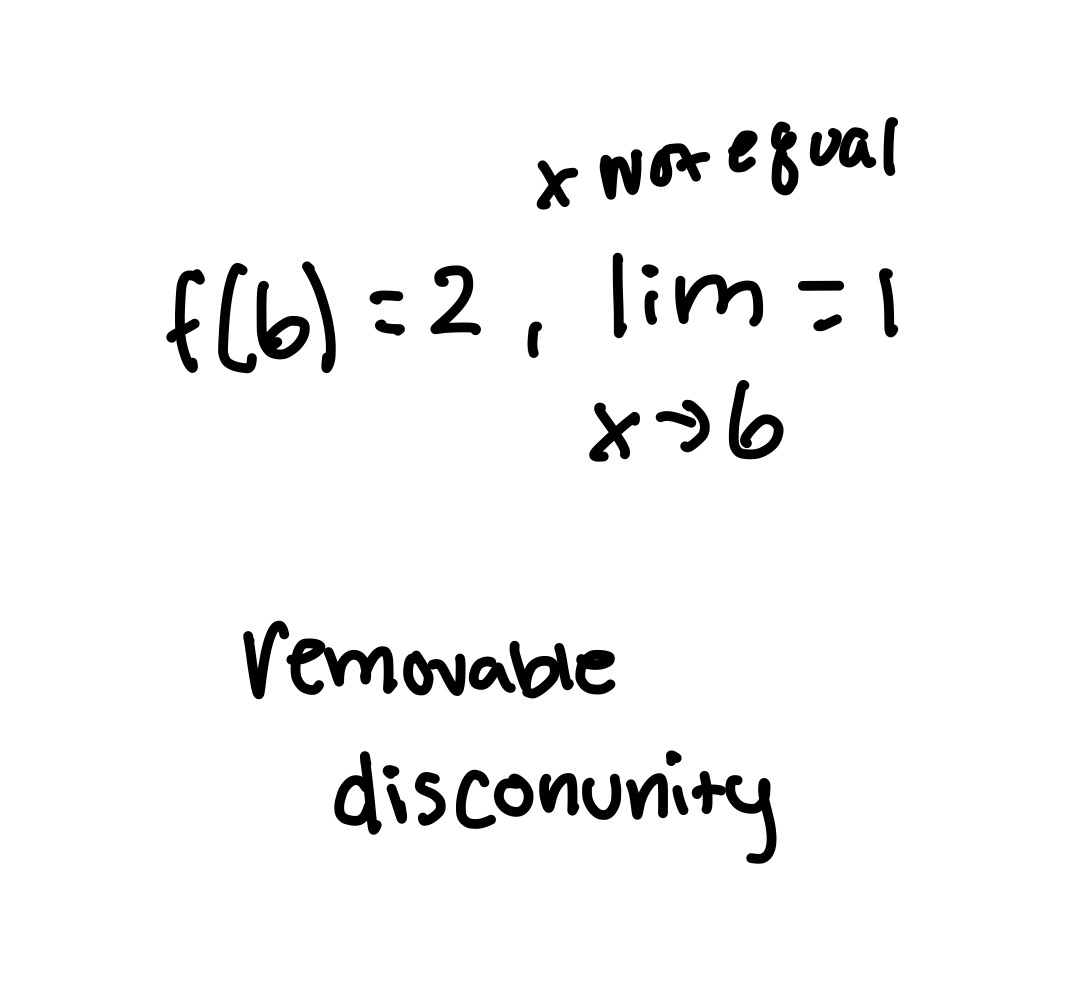
15
New cards
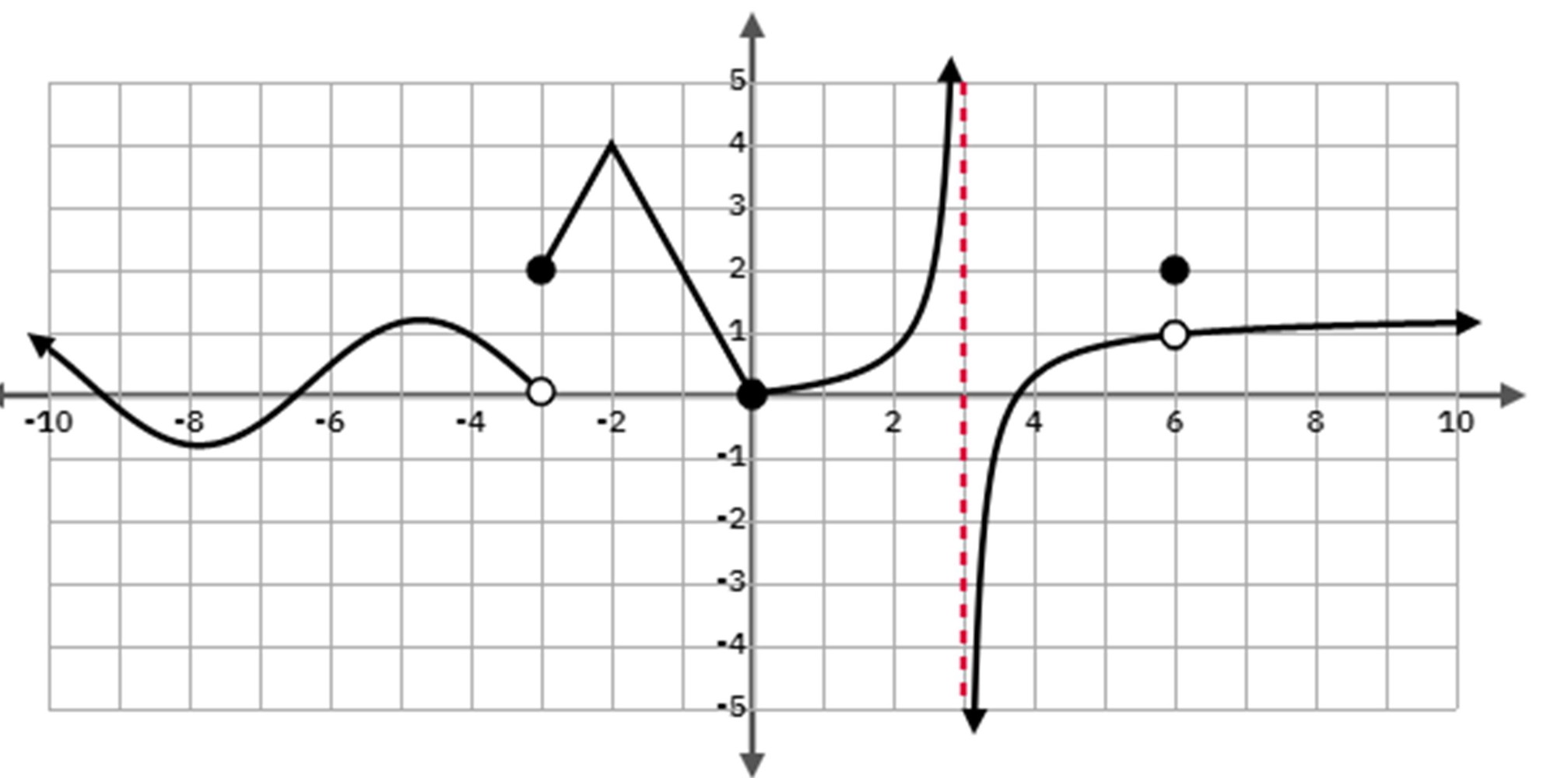
Discontinuity: Jump
Where you have a gap( break) between the line and you would have to go up or down to continue

16
New cards
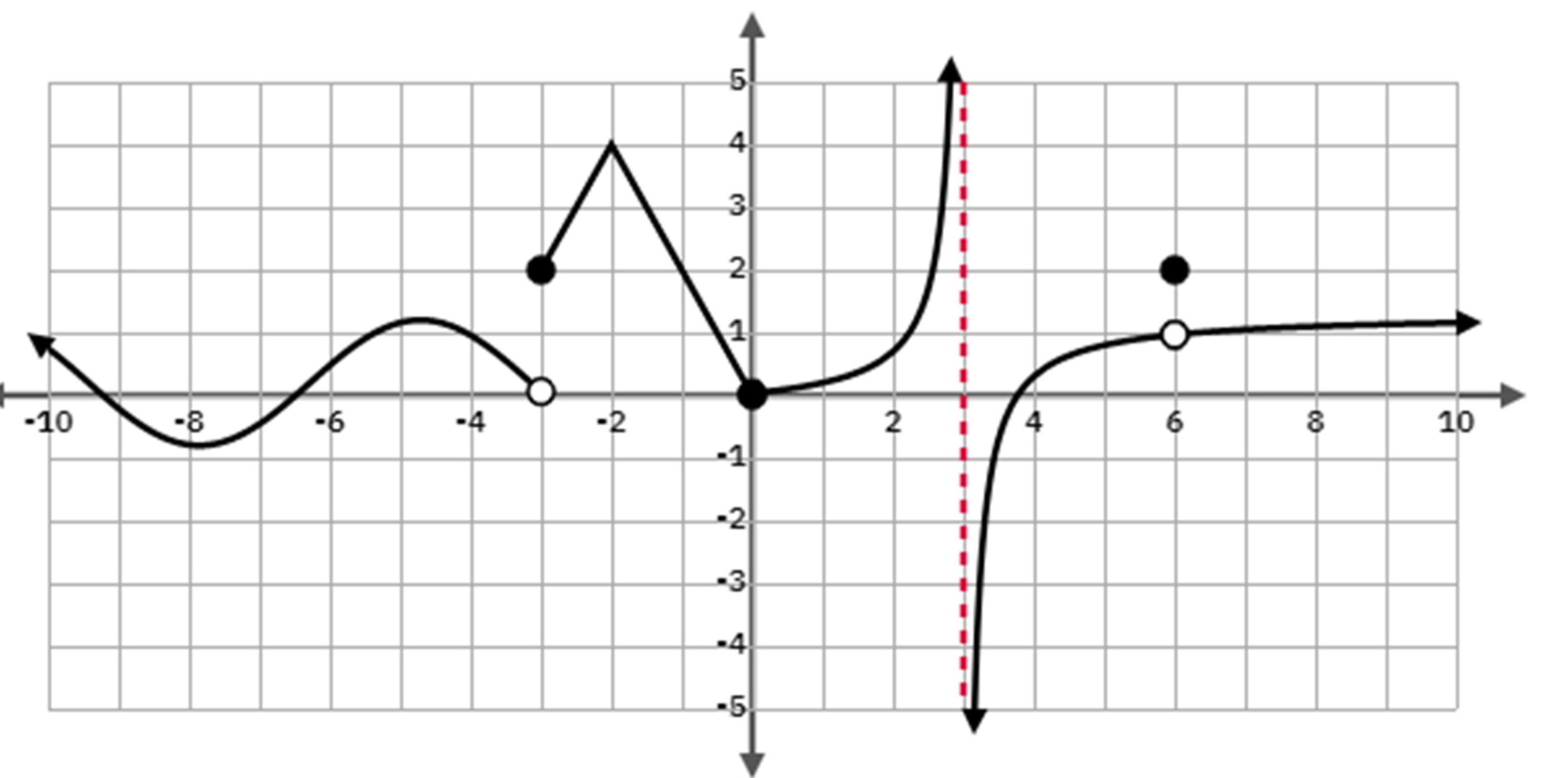
Discontinuity: Infinite
An asymptote is usually a good indicator, but it’s when both the function value and limit does not exist in that limit

17
New cards
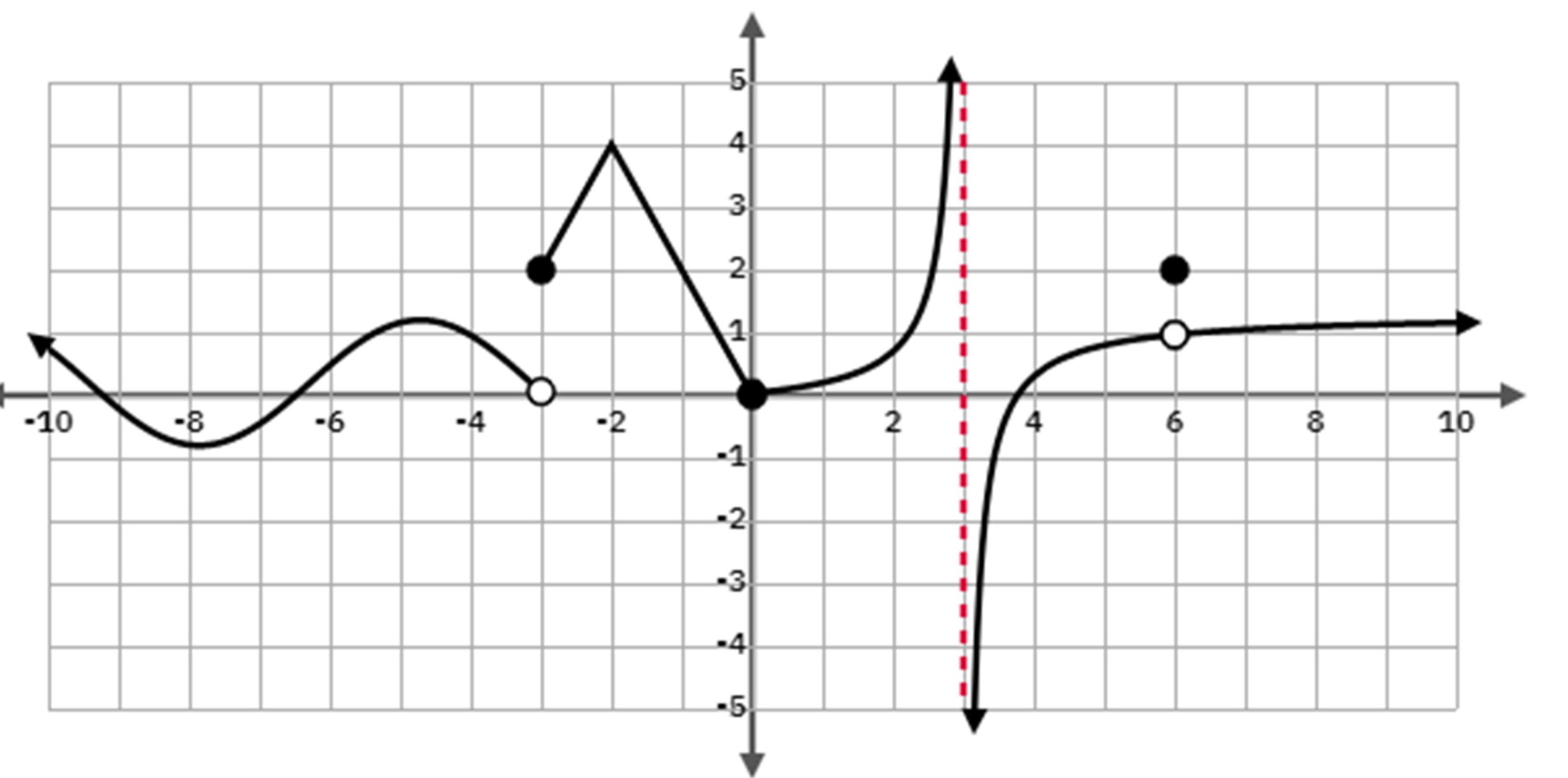
Continuous Domain
Be sure to write and not include anything discontinuous
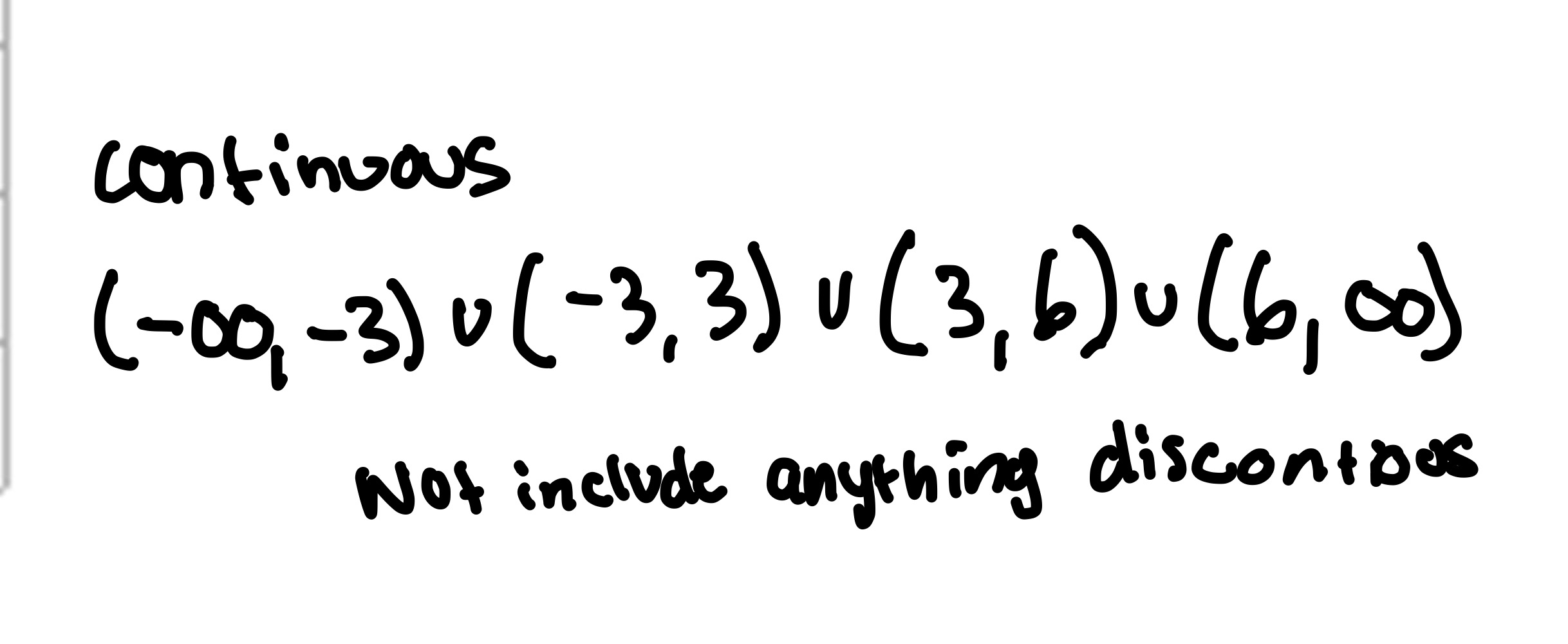
18
New cards
Polynomials + Rational Functions
Polynomials are continuous everywhere(-,+) Rational, root, trig, inverse trig, exponential, logarithmic functions are continuous where defined( every number) in its domain
19
New cards
The Intermediate Value Therem(IVT)
Condition 1: Must be Continuous. 2: N must be between the intervals. 3: That function values don’t equal. To prove the function continuous at the interval.

20
New cards
Degree ratios

21
New cards
Tangent Line Equation
Y=Mx+b ( just find value of m through formulas and solve for b using the points for x and y.
22
New cards
Position and Velocity
S(t)= S( t2)-S(t1)/ t2-t1 : Distance/ time
23
New cards
Instantaneous Velocity
S’(t)=v(t)
24
New cards
Refer to Notes
Go to page 36( second page of 2.8) study how you make those graphs
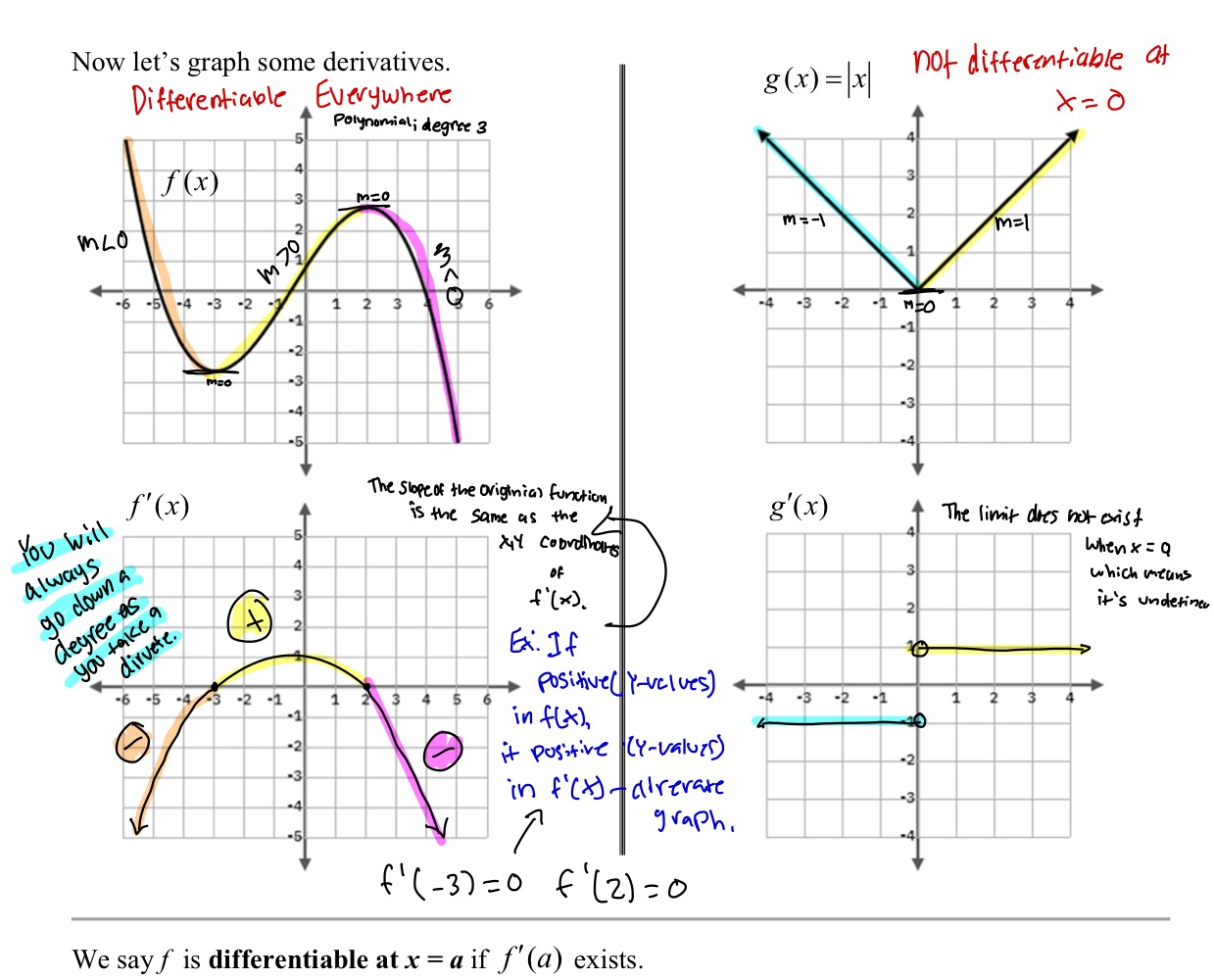
25
New cards
Theorem
If f is differentiable at a, then f is continuous at a. NOT! The other way around