Unit 3 -- Trigiometry / unit circle basics

Pre-calc

Write these special angles of quadrant I in radians:

• 0°

• 30°

• 45°

• 60°

• 90°

• 0° = 0

• 30° = π/6

• 45° = π/4

• 60° = π/3

• 90° = π/2

Write these special angles of quadrant II in radians:

• 120°

• 135°

• 150°

• 180°

• 120° = 2π/3

• 135° = 3π/4

• 150° = 5π/6

• 180° = π

Write these special angles of quadrant III in radians:

• 210°

• 225°

• 240°

• 270°

• 210° = 7π/6

• 225° = 5π/4

• 240° = 4π/3

• 270° = 3π/2

Write these special angles of quadrant IV in radians:

• 300°

• 315°

• 330°

• 360°

• 300° = 5π/3

• 315° = 7π/4

• 330° = 11π/6

• 360° = 2π

Make the table for the unit circle trig values + the ASTC graph view

It should look like:

• Q1 – All: sin, cos, tan all positive

• Q2 – Students: sin is positive (cos, tan neg)

• Q3 – Take: tan is positive (sin, cos neg)

• Q4 – Calculus: cos is positive (sin, tan neg)

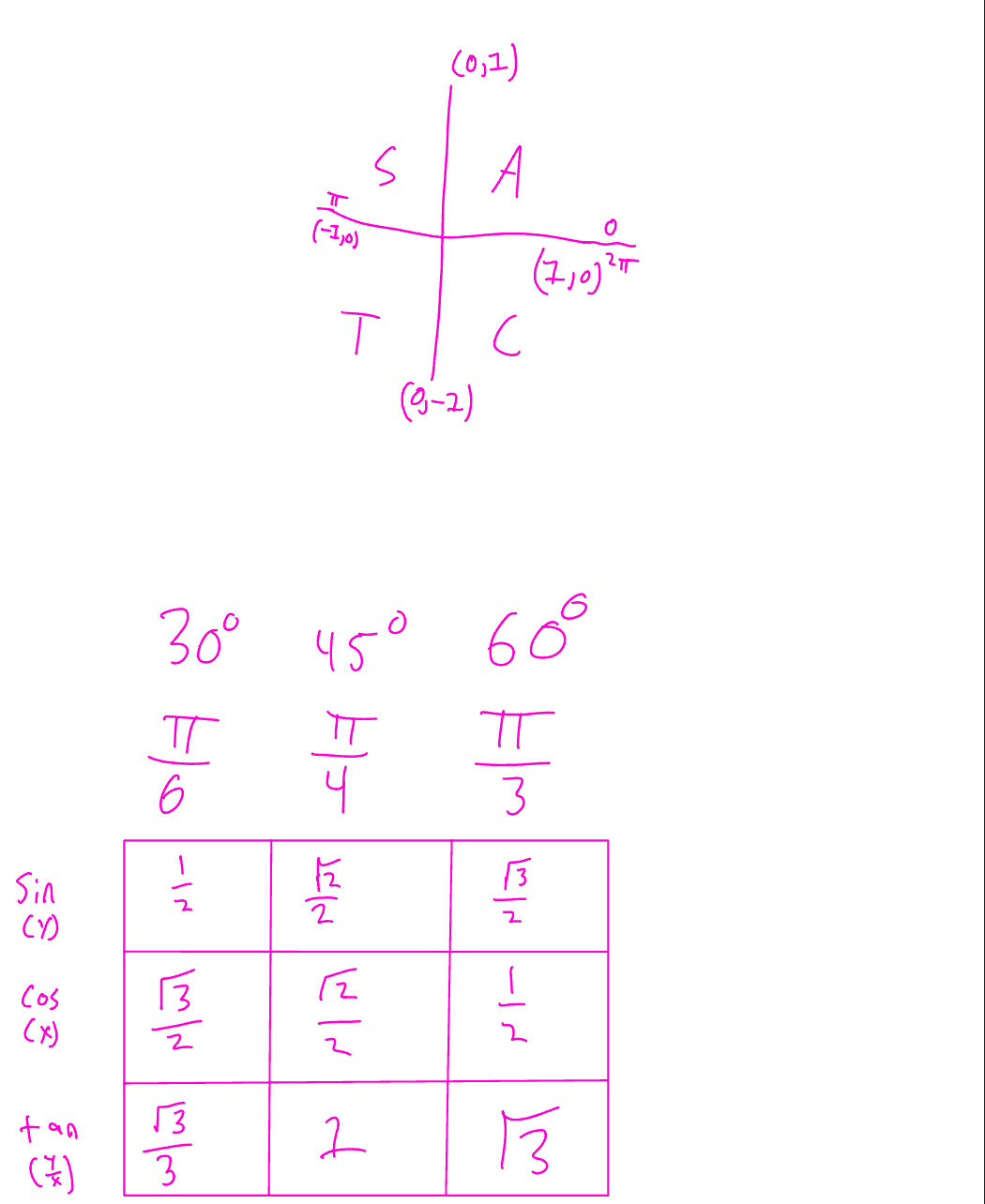
What are reference angles and write the following formula for reference angles in Quadrants I, II, III, and IV:

Reference angle in Quadrant II:
π – θ

Reference angle in Quadrant III:
θ – π

Reference angle in Quadrant IV:

2π – θ

What are coterminal angles and how do you find them?

• Add or subtract 2π (or 360°) until it's between 0 and 2π.

sin(–θ) = ?

–sin(θ)

cos(–θ) = ?

cos(θ)

tan(–θ) = ?

–tan(θ)

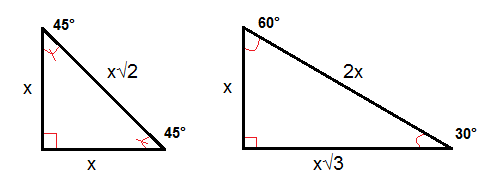
Write the ratios for 30-60-90 and 45-45-90 triangles:

30-60-90

• Opposite 30° = 1

• Opposite 60° = √3

• Hypotenuse = 2

45-45-90

• Legs = 1

• Hypotenuse = √2

r = ?

• unit circle r=1

• any other circle: r= √x²+y²

sinθ=?

y / r

cosθ = ?

x / r

tanθ = ?

y / x

What does “standard position” mean?

Initial side at positive x-axis; rotate counterclockwise.