Pure Maths

Transformation y = |f(x)|

Negative values of y are reflected in x-axis

Transformation y = f(x) + a

+a in y-axis

Transformation y = |f(x)|

Negative values of y are reflected in x-axis

Transformation y = f(x) + a

+a in y-axis

Transformation y = f(x + a)

-a in x-axis

Transformation y = af(x)

All y-coordinates ×a

Transformation y = f(ax)

All x-coordinates ÷a

Transformation y = -f(x)

Reflection in x-axis

Transformation y = f(-x)

Reflection in y-axis

When is a binomial expansion valid (yr13)?

For (a + bx)ⁿ, valid when | bx/a | < 1

or |x| < a/b

x = aⁿ as a log?

n = log_ax

log_a (x^k) rearranged

klog_ax

log(xy)

log(x) + log(y)

log(x/y)

log(x) - log(y)

Order of transformations

x: reflect, stretch, translate | y: translate, stretch, reflect , modulus

π Radians in degrees

180

Condition for increasing function?

dy/dx ≥ 0

Condition for decreasing function?

dy/dx ≤ 0

Condition for local minimum?

d²y/dx² > 0

Condition for local maximum?

d²y/dx² < 0

Condition for concave function?

d²y/dx² ≤ 0

Condition for convex function?

d²y/dx² ≥ 0

Percentage Change

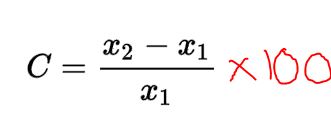
Area of circle segment

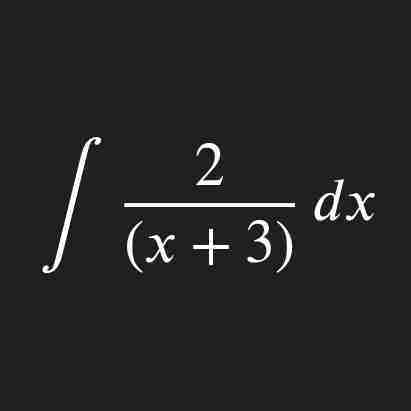
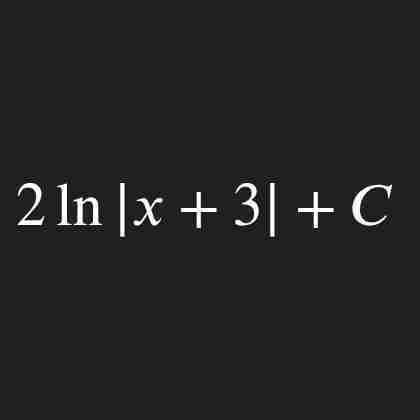
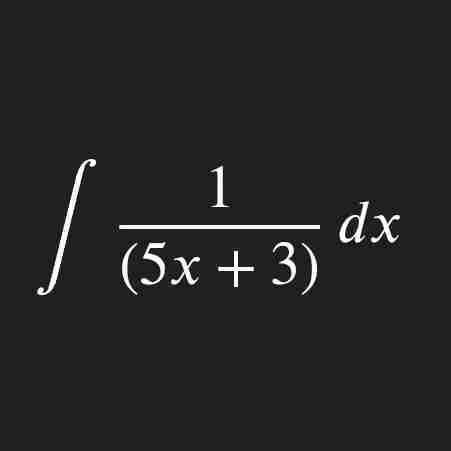
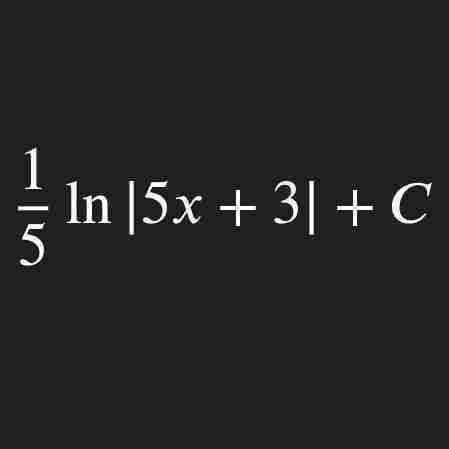
How to integrate a parametric function?

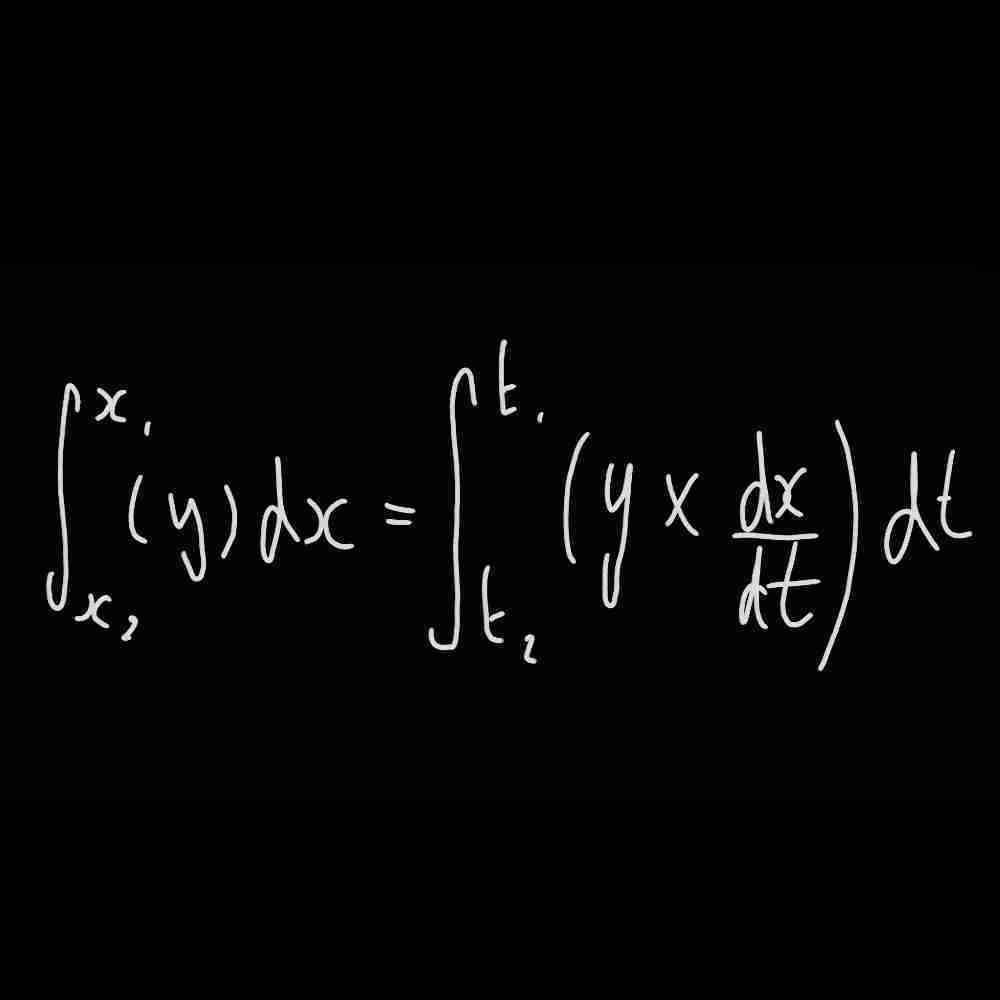
Differentiate

y = ln(5x)

dy/dx = 1/x

Graph of sec x

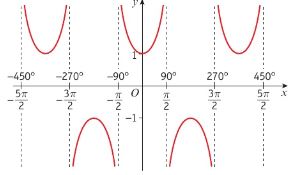
Graph of cosec x

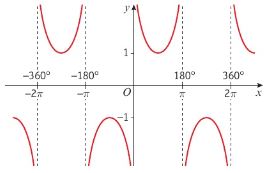
Graph of cot x

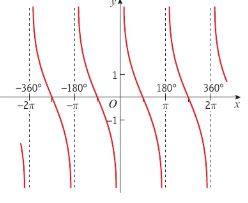
Domain and range of sec x

Domain: x ∈ R, x ≠ any odd multiple of 90

Range: between -1 and 1

Domain and range of cosec x

Domain: x ∈ R, x ≠ any multiple of 180

Range: between -1 and 1

Domain and range of cot x

Domain: x ∈ R, x ≠ any multiple of 180

Range: y ∈ R

Differentiate y = a^kx

dy/dx = a^kx k ln(a)

nth term of a geometric sequence

ar^n-1

Equation for length of a line

[ (x₂ - x₁)² + ( y2 - y1)² ]^1/2

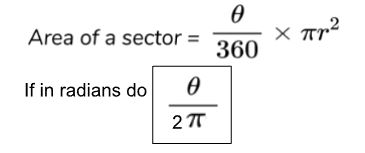
Arc Length equation

arc length = 2πr × (θ/360)

if in radians then (θ/2π)

What is ‘n’ for trapezium rule?

Number of rectangles

If for trapezium rule 5 ordinates are used to approximate area, what would n be?

n = 4

Area of a triangle (not 1/2bh)

½(a)(b)(sinC)

cos rule for triangles

a² = b² + c² - 2(b)(c)(cosA)

Integral of f’(x) × f(x)^n

f(x)^(n+1)

÷ n+1

What makes a function a function?

If it is one-to-one or many-to-one

ie NOT one/many - many

When sketching two ranges e.g f(x) = 5 - 2x for x < 1 and = x² + 3 for x>=1, how do you represent these inequalities?

• Draw both graphs up to limits

• Use a coloured in circle for =

• Use a not coloured in circle for < or >

• Join the circles with a straight line

Limitations of change in sign method

• There can be a change in sign but not root if the graph is not continuous e.g 1/x

• There can be no change in sign but a repeated root if it touches the axis

• There can be no change in sign because the points are too spread apart so there are e.g two roots between them

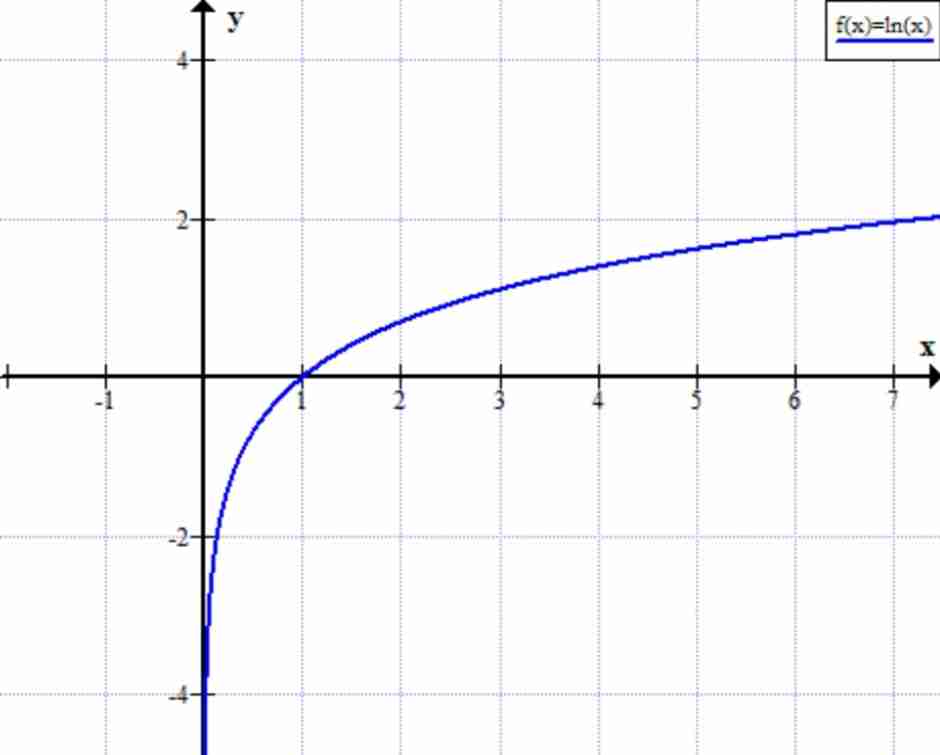
Graph of y = ln x

When does Newton-Raphson fail?

• If f’(x) gives zero it means x0 (first number being inputted) is a stationary point so the gradient is zero, therefore the tangent at x0 is a horizontal line and won't cross the x-axis so no x1 is produced

• Iterations are diverging

• Iterations converge to another root

When does a function have an inverse?

When the function is one-to-one

Volume of a cone

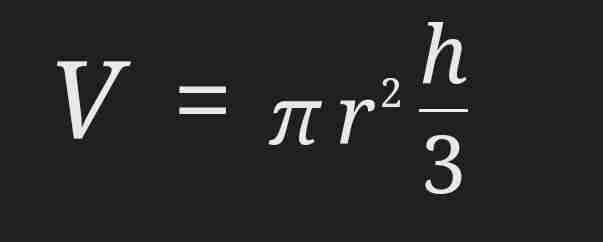
Volume of a cylinder

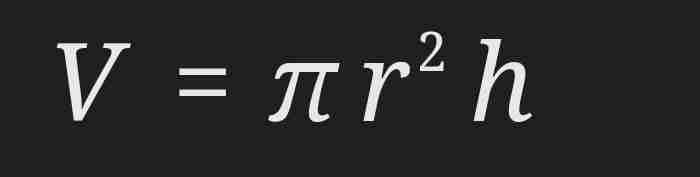
Volume of a sphere

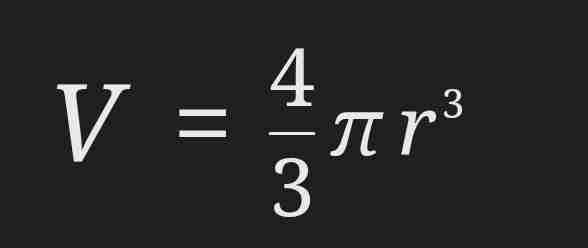
Surface area of a sphere

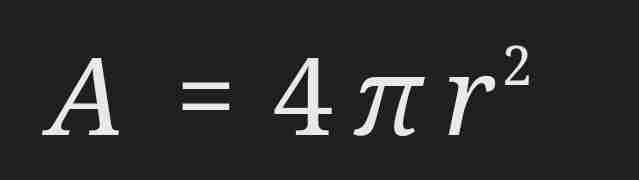
Types of triangle

• Equilateral - all sides equal

• Isosceles - two equal sides

• Scalene - all sides are different

• Acute triangle - all angles > 90°

• Obtuse triangle - one angle < 90°