queuing

reasons for wait

• servers

  • not enough

  • too slow

• customer

  • too many

  • people arriving before you

business perspective

• should reduce amount of time customers wait

customer perspective

• find queues to be fair cuz served in the order you arrive

queuing models

• gives the amount of service you should be providing

  • affected by wait times which can be mitigated by # of employees

    • more = shorter line but more labor expense

    • less = longer line but more cost of unhappy customers

• units

  • entity that waits in queues

  • ex.

    • customers

    • commuters

    • jobs

    • printers

    • subassemblies in manufacturing

    • emails

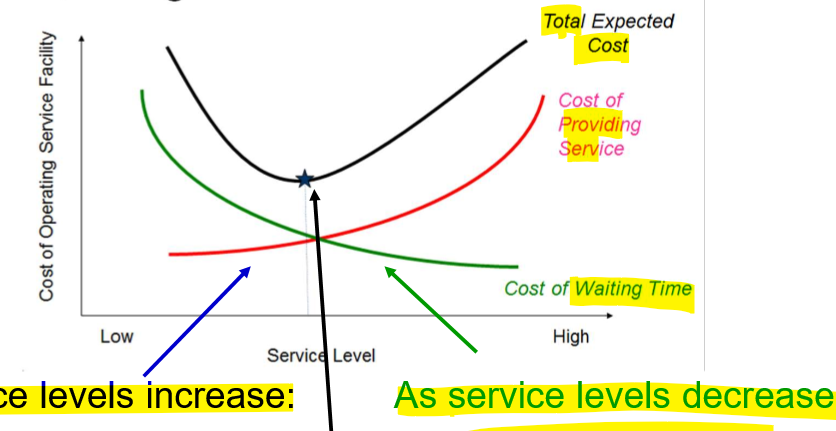
trade-offs in queuing models

• graph

  • queuing costs (service and unhappy customers) v. service levels

  • optimal service level

    • not directly above cost intersect

    • cuz not found through formula

• as service inc.

  • cost of service inc. but cost of unhappy customer dec.

• as service dec.

  • cost of service dec. but cost of unhappy customers dec.

performance measures

• used to determine:

  • effect of changing # of servers

  • Effect of changing arrival rate

  • effect of reducing avg. service time

• to eval. efficiency and effectiveness

• types

  • avg. # of customers waiting in line

  • avg. # of customers in system

  • avg. waiting time in queue

  • avg. time in system

line-up actions

• customers will do one of the following

  • wait in line

  • not join the line

    • leaving right away

  • jockey

    • when multiple lines

    • if find that ur line is too long and the other is shorter, then move to it

  • initially join the line then leave

  • meld

    • multiple lines become one big line

queuing theory

• deals w/ queues

• in early 1900s by A.K. Erlang

  • through studying congestion and waiting times on phone lines

psyc. tips for queue manage.

• perception of wait

  • tendency to overestimate waiting time

  • feels longer than it is

• acceptable waiting time depends on:

  • type of service

    • urgent or no?

  • type of waiting

    • in person v. through phone

      • more willing if in person cuz already allocated time and effort to the endeavor

  • type of customer

    • do they have kids w/ them?

• distractions

  • provide them

  • things to do

  • ex.

    • tv.

    • magazines etc.

• avoid line-up whenever possible

  • plan for the endeavor beforehand

  • through ex.

    • appointments etc.

• whether to provide awareness of time?

  • provide only if customer is unable to do it themselves

  • ex.

    • position in phone line

    • time till boarding a plane

• modify arrival behav.

  • incentives to come at non-peak hours

  • ex.

    • make it cheaper etc.

• idle resources out of sight

  • dont let customers see staff not doing anything

• segment customers

  • into who will wait vs. who is willing to pay extra to not wait

  • only if high volume

• think long term

  • dont let long lines be apart of ur company’s reputation

• friendly server

  • alter the impression of the wait

  • ex.

    • apologize for the wait

disneyland ex. of dealing w/ queues

• park pass can be used to virtually line up for an attraction

  • it will tell you what time your turn will be at

  • a way of making you do other things (that will cost money) while waiting

• tell what times are busy for diff. meal times

• virtual queues for restaurant

  • will tell you when they’re ready for you and food will already be ready by the time you get there

queuing configurations

• follow FCFS

  • first come first serve

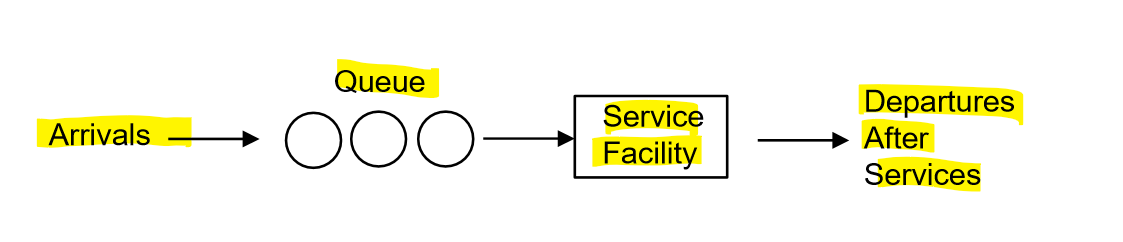
• parts of a queuing system

  • arrivals → queue → service facility (where the service itself occurs) → departure after services

• defined by # of channels/servers and # of phases

• types:

  • singe server, single phase

  • single server, multi-phase

  • multi server, single phase

  • multi server, multi phase

single server, single phase

• 1lineup and 1 server

• ex.

  • one banking machine

  • a car wash

  • small business w/ one cashier

  • a dive board at a pool

single server, multi-phase

• 1 lineup leads to 1 server then from there another lineup leads to another server that provides the main service

• ex.

  • fast food drive-thrus

    • 1st asks for your order

    • 2nd gives you the food

  • assembly lines

multi server, single phase

• 1 lineup leads to multiple server of which you choose 1

• ex.

  • bank tellers

  • checking in at an airport

• NOT like in a big grocery store

  • multiple separate lines

    • that are single server, single phase

multi server, multi phase

• 1 line leads to multiple servers of which you choose one who then pass you over to a type 2 server that will complete the service

• ex.

  • health care

  • auto repair

  • job shops

calling pop.

• where arrivals come from

• character. (each has alternatives):

  • size

    • big / infinite

      • most common

      • # in line < # that could come to line

    • small /finite

      • pre-set max. that can join line

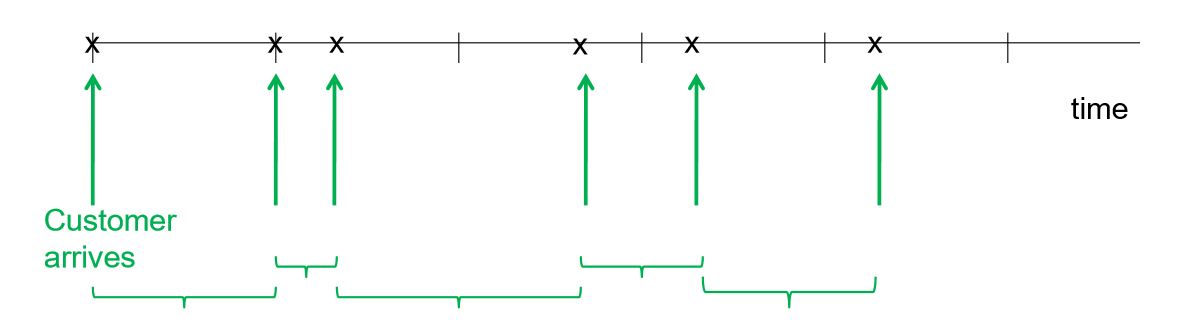
  • arrival pattern

    • distribution

      • random

        • poisson

        • based on independent arrivals

      • pre-determined

        • based on appointment

  • attitude

    • patient

      • will wait

    • impatient

      • will leave w/out service

      • through

        • balking

          • not joining line at all

        • reneging

          • join and then leave

the system

1. customers arrive to it at a random time

2. then, either:

   • if server idle, customer receives service right away

   • if server busy, customer must wait in the queue before being served

3. then time is taken to process customer

4. customer leaves system when finished

• queue time + service time = system time

• to describe and calculate performance need to know

  • prob. distribution of inter-arrival times

  • prob. distribution of service times

  • number of servers

avg. arrival rate

• denoted as:

  • lambda λ

• avg. # of customers arriving in a time period

• modelled by poisson distribution

  • because time between arrivals is independent

  • so should be an integer

• ex.

  • 2 arrivals per minute

  • λ = 2

poisson prob. distribution

• the prob. of x customers arriving in a time period

• P(x) = ((λ ^x)*(e^-λ ))/x!

  • x = the actual number of arrivals

  • λ = the mean/ avg. # of arrivals

  • will give a percentage

avg. inter-arrival time

• 1/ λ

• modelled by exponential distribution

  • so does not have to be an integer

• ex.

  • 2 arrivals per minute

  • λ = 2

  • inter-arrival time

    • 1/ lambda = ½ minutes

    • in seconds

      • 60 seconds/ lambda

      • 60 seconds/ 2 = 30 seconds

• this is what causes a queue to form

avg. service rate

• # of customers that can be served by 1 server

• denoted as:

  • mu μ

• follows the poisson distribution

• ex.

  • serve 3 customers per minute

  • μ = 3

avg. service time

• the time needed to provide the service

  • does not include queue time

• denoted as

  • 1/μ or 1/ service rate

• follows the exponential distribution

• ex.

  • serve 3 customers per minute

  • μ = 3

  • service time = 1/μ = 1/3 minutes

    • to get seconds:

      • 60 seconds/ μ

      • 60 seconds/ 3 = 20 seconds

prob. distribution of service time

• P(service time <=t) = 1-(e^-μt)

• to solve:

  • make sure the service rate, service time and t is in the same units

  • per hour, minutes etc.

variability

• if arrivals are less than amount of people servers can serve, easy to assume that there should not be any waitin in line

  • NOT TRUE

    • the quantities are only avg.s so in real life there can be more arrivals in certain time periods than others or some service times are taking too long compared to others

    • therefore, no guarantee that there will not be a line

kendall notation

• describes the character. of a queuing model

• M/ /

  • most common: M/M/1

    • 1st M

      • prob. distrib. for arrival process

        • poisson

    • 2nd M

      • prob. distribution for service time

        • exponential

    • 1 = # of servers

    • use when:

      • customers arrive w/out appointments

      • system is stable

      • first come first serve

      • no balking or reneging

      • system has reached a steady state

  • M

    • markovian* inter-arrival times

      • markovian = arrival+service or poisson+exponential

• M/M/3

  • 3 servers

queuing theory elements

• s = # of servers

• lambda = avg. arrival rate

• mu = avg. service rate

• first in, first out

  • first come first serve

idle time

• w/in a time period

• time between end of service and arrival time of next service * number of customers

total work time

• reciprocal of idle time

• service time*#of customers

how queues form

• occurs when there’s a lagging in the system

• components of chart

  • customer #

  • arrival time

  • # in system

  • wait

    • duration

  • start time

  • service time

    • duration

  • end time

• start time = end time of last customer

• wait = start time - arrival time

• if balking occurs

  • from wait → end time

    • - - - -

• if reneging

  • from start time → end time

    • - - -

    • the time they waited will be under wait time

  • next person’s start time = end time of person before reneger

steady state

• at start of day start at an “empty and idle” state then business activity increases till you reach a normal or steady state of operation

• observed rate of arrival = avg. rate of arrival = lambda

• steady- state can occur at diff. times

  • ex.

    • restaurants reach at lunch and dinner time

    • traffic reaches at morning and evening

stable system

• when:

  • lambda<mu

  • arrival rate is less than service rate

utilization (U)

• U = p = lambda/ (# of servers*mu)

  • make sure arrival and service rate are in the same units

  • p = traffic ratio

    • if less than 1, system is stable

      • if not queue explodes → too big

• % of time servers are busy

• high U is good if the units are items not people

M/M/1 performance measures

• utilization rate(%)

  • U = λ/μ

• prob of 0 customers(%)

  • % of time servers are not busy

    • aka idle time

  • Po = 1-(λ/μ )

  • OR

  • Po = 1 - U

• prob. of a customer waiting (%)

  • customer waits when server is busy in M/M/1

    • Pw = U

    • OR

    • Pw = 1 - Po

      • λ/μ

• avg. # of customers in queue (units)

  • Lq = λ²/(μ(μ-λ))

  • OR

  • Lq = L-(λ/μ)

    • Lq = L - U

• avg. # of customers in system (units)

  • in queue + being served

  • L = Lq +λ/μ

    • L = Lq + U

  • OR

  • λ/(μ-λ)

• avg. time customer in queue

  • in time in same units as given in og problem

    • ex. to get minutes from hours

      • hours* minutes in an hour = minutes

  • Wq = Lq/λ

  • OR

  • W - service time

    • W - 1/ μ

  • OR

  • λ/ (μ(μ-λ))

• avg. time customer in system

  • in time in same units as given in og problem

  • in queue + being served

  • W = L/λ

  • OR

  • W = 1/(μ-λ)

  • OR

  • w = Wq + service time

    • W = Wq + 1/μ

• prob. of n customers in system

  • prob. of an exact amount

  • Pn = (1-(λ/μ ))*((λ/μ ) ^n)

  • OR

  • Pn = Po*(U^n)

• prob. of more than k customers in system

  • Pn>k = (λ/μ ) ^k+1

  • OR

  • Pn>k = U^k+1

Q.xls

• calc. performance measures for M/M

  • where s can be any number of servers

• expected = avg.

decision making for queues

• answers:

  • how busy should a server be

    • tradeoff between higher server utilization and long queues

  • multiple single-server queues v. multiple server queue

  • do we need more servers

  • increase service speed v. inc. servers

how busy should a server be

• ex.

  • service time = 6 minutes

    • work backwards to get mu

      • (60 minutes/ hour)*(1 service/6 minutes = 60 services/ 6 hours = 10 service/hour

      • so, service rate = 10

    • when comparing diff. arrival rate up to 10 and seeing U, Wq (time in queue), and Lq (people in queue)

      • observation 1: when U too high, Wq and Lq get extremely high

        • can save resources but too much system congestion

      • observation 2: up to around 70% U, no sig. changes in Wq or Lq till then

• to reduce wait time need to reduce variation

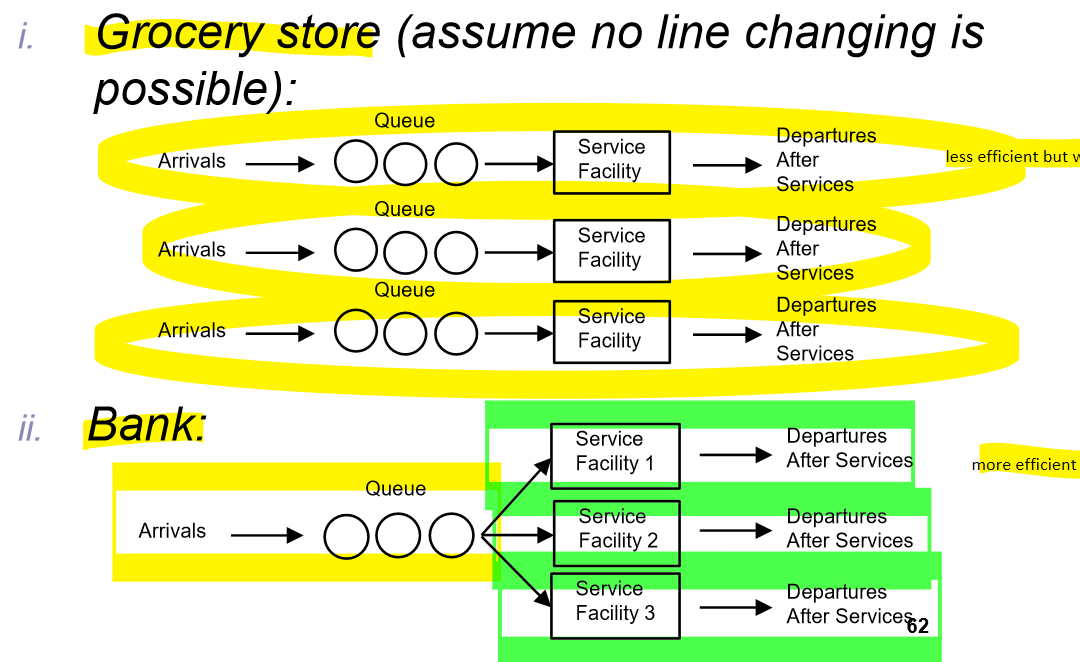
multiple single-server queues v. multiple server queue

• multiple single server

  • less efficient

    • cuz cant switch lines (jockey)

  • but good if:

    • you want customer to be engaging in other things like buying

    • if want to reduce traffic

    • there’s a prep time needed

      • ex. putting things on a conveyor belt beforehand

  • mostly used in grocery stores

• multiple server queue

  • if goal is to get through most people as fast as possible

  • more efficient

  • ex. used in banks

  • can be enforced

    • cash machines

    • washroom stalls

    • fast food

• between both

  • U will be the same but all other performance measures will be diff.

do we need more servers (eCycle case Study)

• ex.

  • received $30,000 waiting fee

    • between when city trailers get to facility and service begins

    • a $60/ hour fee for waiting at the dock including unloading

  • 1 loading dock

  • 2 employees

    • paid $24/ hour

  • mu = 4 per day

  • lambda = 3 per day

  • need to answer 3 things:

    • how long do the trailers wait at the late of 60/ hours

      • is the 30,000 invoice correct

      1. find W (avg. time (days) in system)

         1. 1/(μ-λ) = 1/ (4 - 3) = 1 day

      2. find L (avg. # of trailers in system)

         1. λ/(μ-λ) = 3/(4-3) = 3

      3. use 1 and 2 to get cost per day

         1. 3 trailers per day for 8 hours a day for $60 per hour

         2. 3×8×$60 = $1440

      4. get weekly

         1. $1440×5 = $7200

      5. get monthly

         1. (52 weeks/ 12 months)*$7200 = $31,176

            1. therefore, 30,000 invoice is correct

    • what are the current costs

      • are the trailers or the employees more expensive

      1. get cost of workers per day

         1. 2 workers work for 8 hours a day at a rate of $24 per hour

         2. 2×8*$24 = 384

      2. get weekly

         1. $384×5 = 1,920

      3. get monthly

         1. $1,920*(52 wks/12 months) = $8,314

      4. compare to the 31,176 you got for the trailers

         1. conclude that more costs come from trailer

            1. around 79%

            2. cen reduce by getting more crew

    • how does the change in crew size affect costs and what is the optimal crew size

      1. assuming that each extra worker = 1 more trailer unloaded per day

         1. go through step 1 again while adding the 1 extra worker until the total daily cost hits a minimum

• other process improvements

  • lower unloading time

    • through use of pallets or conveyor belts

  • increase loading docks

  • dont use city trailers in the first place

  • have them arrive by appointment/ set times

  • flexible crew size

    • other people can come help if one is taking too long

increase service speed v. inc. servers

• depends on:

  • if want to shorten wait time = add server

  • if want to shorten service time = speed up service

using queuing theory v. simulation

• simulation

  • more accurate

  • performance measure more extensive

  • more flexible

    • can be used in many situation

• queuing theory

  • more convenient

    • dont need software

  • quicker

  • dont need tech