MM - Chapter 7: Lossy Compression: Transform coding (copy)

wat is lossy compression

• The compressed data is not the same as the original data, but a close approximation of it

• Yields a much higher compression ratio than that of lossless compression

Measuring and comparing image quality (3 gebruikte maten)

extra psnr shit → niet in slide gdmmit

Hier is een kortere maar volledige versie:

• makkelijk te berekenen

• hoge MSE → meer distorties dan lage MSE

• PSNR vaker gebruikt dan MSE voor gereconstrueerde foto/video kwaliteit:

  • MSE hangt af van woordlengte signaal

  • gemiddelde foto/frame ≠ 0

  • PSNR normaliseert MSE tov pieksignaal → beter vergelijkbaar tussen codecs/systemen

  • PSNR ≥ 0

• PSNR kan misleiden:

  • kleine phase shift → mens ziet niet, PSNR wel

  • visual masking: fouten verstopt in minder opvallende regio’s → hoge subjectieve kwaliteit, maar PSNR merkt fouten toch

  • fouten spreiden over tijd

  • vergelijkingen tussen verschillende coderingsstrategieën

(nogmaals) wat is quantization in de context van lossy compression?

Wat zijn de drie main forms van quatization?

• Verminder het aantal verschillende uitvoerwaarden tot een veel kleinere set

  • vb. van analoog naar digitaal (cf. hoofdstuk 5)

  • hier: kwantiseer al gedigitaliseerde samples om het dynamisch bereik te verkleinen

• Belangrijkste bron van “verlies” in lossy compressie

• Drie hoofdvormen van kwantisatie

  • uniform: midrise- en midtread-kwantisatoren

  • niet-uniform: companded-kwantisator, Lloyd-Max

  • vector-kwantisati

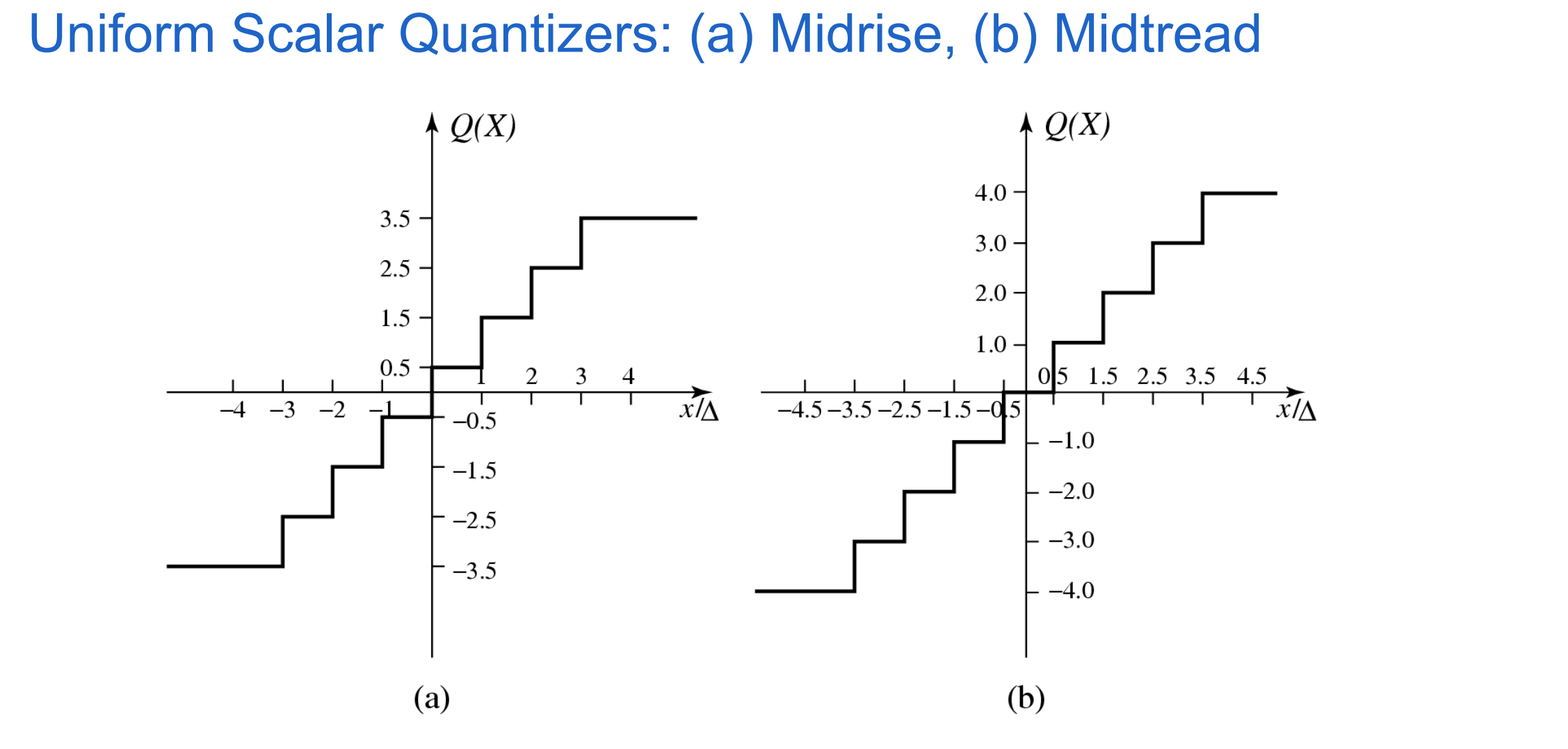
uniform scalar quantization

Een uniforme scalaire kwantisator verdeelt het domein van invoerwaarden in gelijk verdeelde intervallen (behalve mogelijk aan de buitenste intervallen)

• lengte van elk interval = stapgrootte, aangeduid met het symbool Δ

• de uitvoer- of reconstructiewaarde per interval = typisch het midden van dat interval

Twee types uniforme scalaire kwantisatoren:

• midrise-kwantisatoren: even aantal outputlevels

• midtread-kwantisatoren: oneven aantal outputlevels, inclusief nul als een van de levels

non-uniform scalar quantization

wanneer 4

soorten 2

Niet-uniforme stapgroottes zijn nuttig wanneer:

• het signaal geen uniforme kansverdeling (PDF) heeft

• signaalbereiken bekend staan om overmatig ruis

• er nood is aan niet-lineaire amplitude-mapping

  • bv. A-law (hoofdstuk 5)

• er gewenst is om een bereik van lage signalen naar nul te mappen

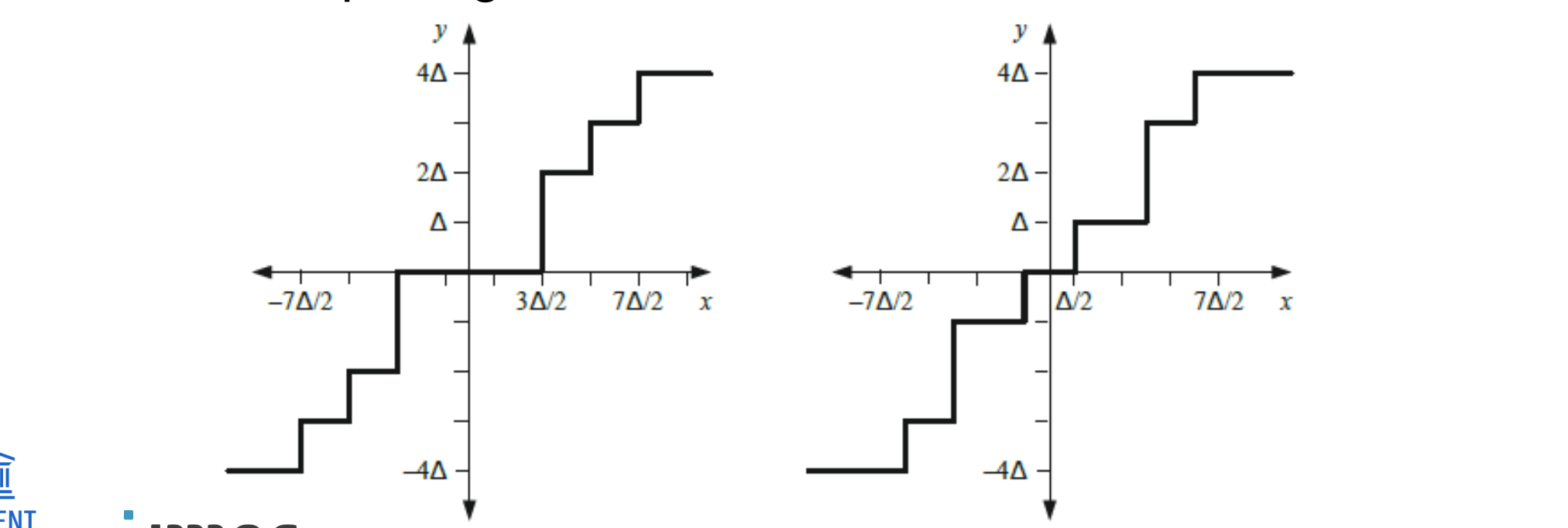
Twee veelvoorkomende niet-uniforme kwantisatoren:

• Deadzone (links)

  • low level signalen niet teveel bits krijgen

• Lloyd-Max (rechts),

  • vervorming minimaliseert door de kwantisator af te stemmen op de kansverdeling (PDF) van het ingangssignaal

vector quantization

Volgens Shannon (informatietheorie):

• Compressiesystemen werken beter als ze opereren op vectoren of groepen van samples, niet op individuele symbolen

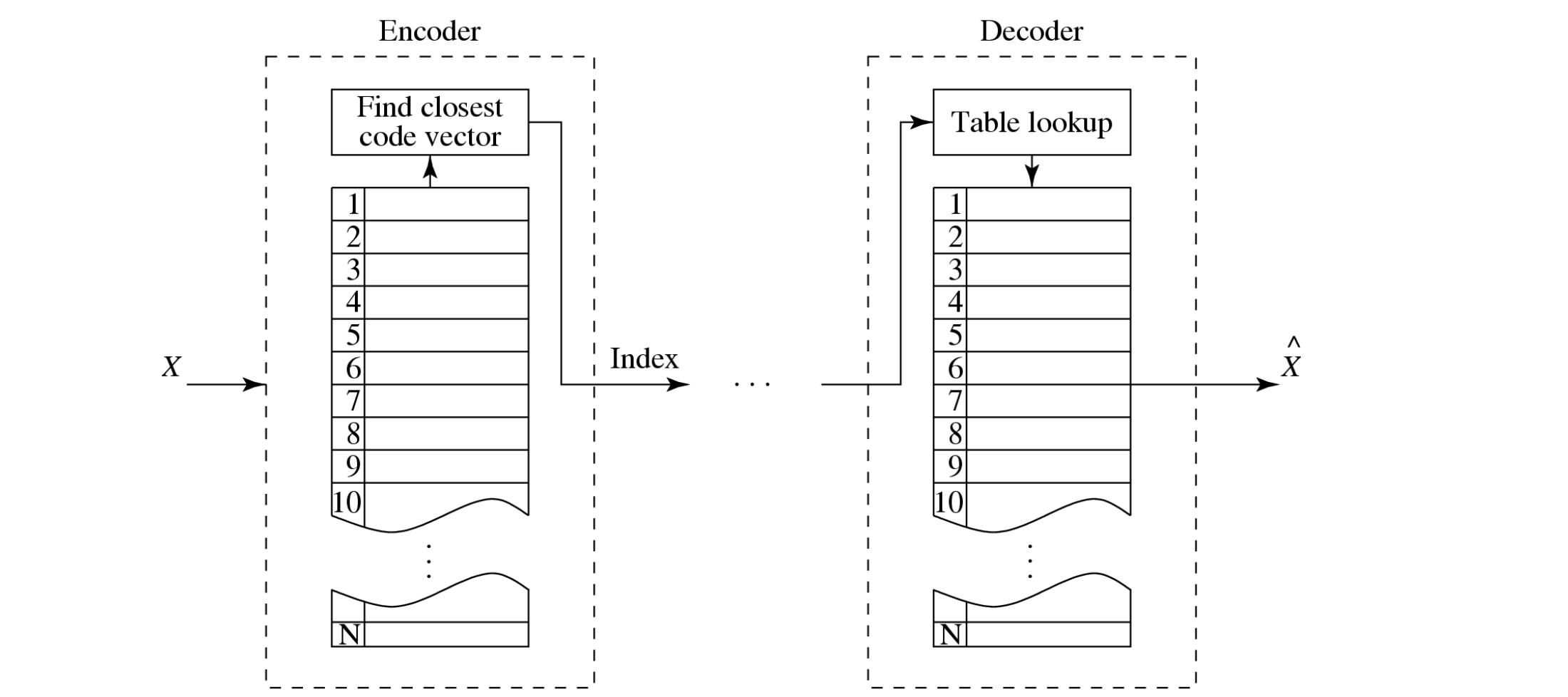
Hoe werkt dit?

• Vorm vectoren van inputs door opeenvolgende samples samen te voegen tot één vector

• VQ (Vector Quantization) definieert een set codevectoren met n componenten

  • in plaats van enkele reconstructiewaarden zoals bij scalair kwantiseren

• Een verzameling van deze codevectoren vormt het codeboek

Rate-Distortion Theory

• afhangt van

• rate-quality curves

• rdo

Framework voor het bestuderen van de trade-off tussen bitrate en vervorming (distortion)

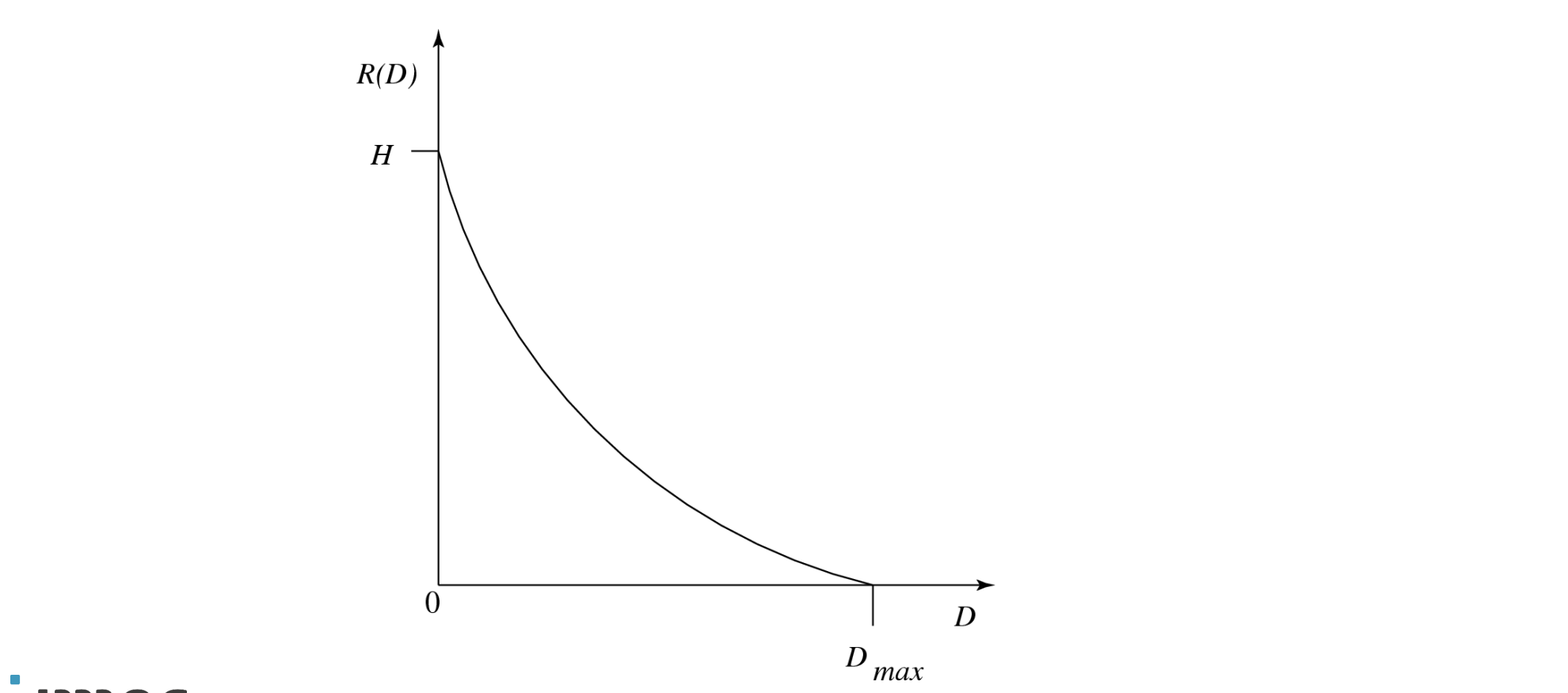
Typische Rate-Distortion functie:

• toont hoe de bitrate R(D) afhangt van de vervorming D

• H = entropie, Dmax = maximale vervorming

Bitrate voor een gecomprimeerde sequentie hangt af van:

• het encodering algoritme

  • differentieel of niet, intra vs. inter, motion estimation, blokgroottes, enz.

• de inhoud

  • veel spatiale of temporele activiteit vraagt meer bits

• de gekozen encodering parameters

  • resolutie, framerate, quantizer, blokgrootte, combinatie van inter en intra, enz.

Vaak worden Rate-Quality curves gebruikt (bijv. PSNR vs. bitrate)

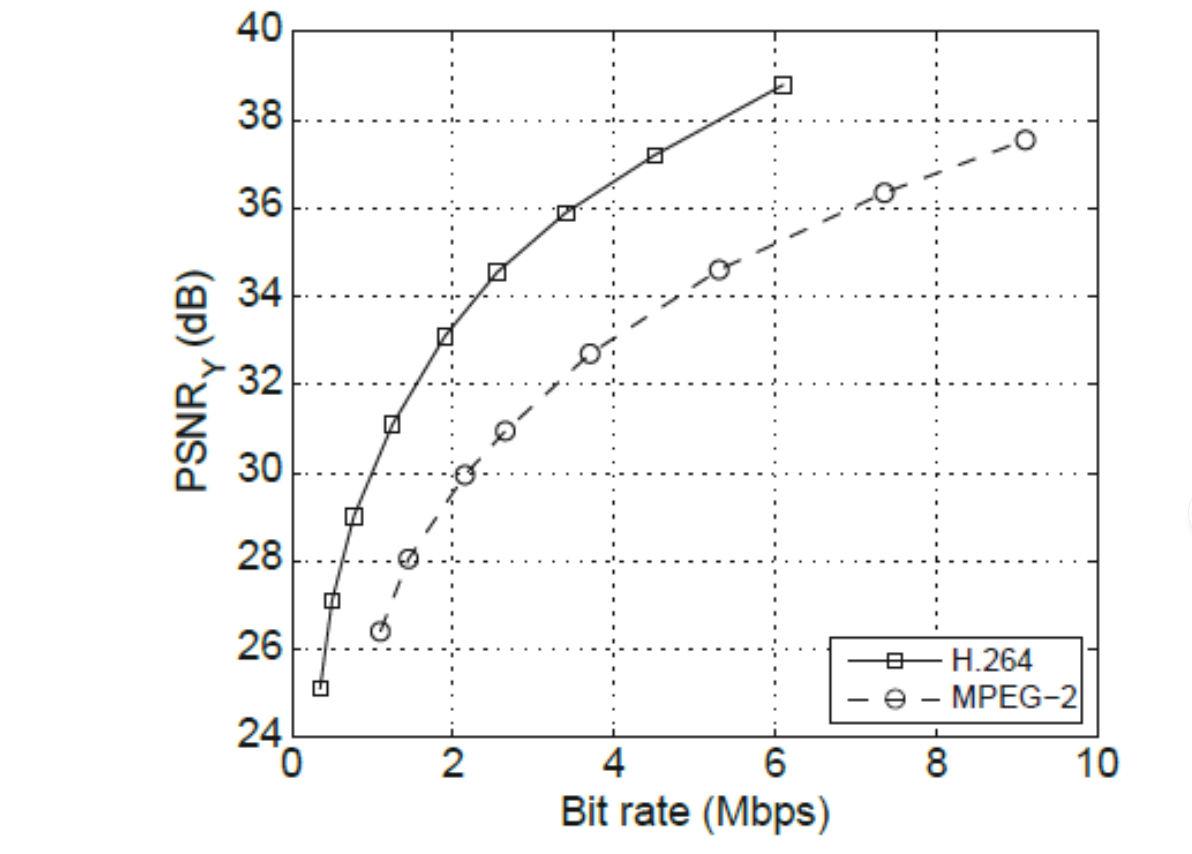
Rate-Distortion Optimization (RDO):

• doel: maximale kwaliteit bij een opgelegde bitrate

• selecteert de beste modes en parameters voor elk deel van het beeld of video

• gebruikt vaak een Lagrangiaan aanpak: minimaliseer D(p) + λR(p), met D = vervorming en R = benodigde bits

• essentieel voor moderne codecs zoals H.264/AVC en HEVC om optimale compressie te bereiken

principles of decorrelating transforms

Transform coding

• Doel: de redundantie in afbeeldingen verminderen door de pixels eerst te decorreleren, zodat de gegevens daarna efficiënter gecomprimeerd kunnen worden.

  • kan een groffere quantisatie stap plaatsvinden

• Achtergrond: in natuurlijke beelden zijn naburige pixels sterk met elkaar gecorreleerd.

Belangrijk:

• De transformatie zelf is verliesloos; compressie ontstaat door quantiseren

• Enkele coëfficiënten bevatten het meeste van de variatie/energie → weinig impact als kleine coëfficiënten verdwijnen

• In praktijk werkt dit op blokken (N × N) om balans te vinden tussen performantie en decorrelatie

Ratiojnale achter transform coding:

• Als C het resultaat is van een lineaire transformatie A op inputvector X, en de componenten van C zijn veel minder gecorreleerd, kan C efficiënter gecodeerd worden dan X

• Als de eerste componenten van de getransformeerde vector bijna alle informatie bevatten, kunnen de andere grofweg gequantiseerd of zelfs op nul gezet worden zonder veel signaalvervorming

  

What did just happen?

• rotating axes effectively decorrelates the data

  • x0 vs. x1 compared to c0 vs. c1

• small values can be set to zero

  • → sparse set of coefficients containing most of the information

• remaining values can be quantized

  • compression (!)

This is the essence of transform-based data compression

stappen van Transform coding

Segmentation

• Verdeelt de afbeelding in N × N blokken (typisch N = 8).
  Dit is een omkeerbare one-to-one mapping.

Transformation (map or decorrelate)

• Transformeert de ruwe inputdata naar een representatie

  • → beter geschikt is voor compressie.

• omkeerbaar (one-to-one mapping).

Quantization

• Vermindert het dynamisch bereik van de getransformeerde output, volgens een kwaliteits- of bitratecriterium

  • psychovisuele redundantie te reduceren.

• Voor ruimtelijk gecorreleerde data geeft dit een sparse blok coëfficiënten.

• Dit is een many-to-one mapping en niet omkeerbaar

  • → basis van lossy compressie.

Symbol encoding (codeword assigner)

• De sparsiteit van de gequantiseerde coëfficiëntmatrix wordt benut (bijv. via run-length coding)

  • reeks symbolen te produceren.
    

• De encoder wijst aan elk symbool een codewoord (binaire string) toe.

  • Het doel is redundantie reduceren (vaak met variabele-lengte codewoorden).

• Deze stap is omkeerbaar.

unitary transform

definitie:

• Een unitary transform is een lineaire transformatie waarbij de basisfuncties orthogonaal en orthonormaal zijn (d.w.z. hun inner product is nul en hun lengte is 1).

• lineaire transformatie die de energie en orthogonaliteit van de signalen behoudt, zodat de inverse gelijk is aan de getransponeerde geconjugeerde matrix

Waarvoor gebruikt / handig:

• Het decorreleert inputdata zodat de energie geconcentreerd wordt in enkele coëfficiënten.

  • totale energie behouden (tussen origineel en getransformeerd)

• Het maakt het mogelijk om met dezelfde matrix (of transponering) de inverse transformatie uit te voeren.

• Het vormt de basis voor efficiënte compressie, omdat kleine coëfficiënten kunnen worden genegeerd of grof gequantiseerd.

HOE?

signaal = lineair combinatie van basis functies

• x = originele vector

• B = in de kolommen basisfuncties

• c = de gewichten →hoeveel van iedere basisfunctie nodig

  

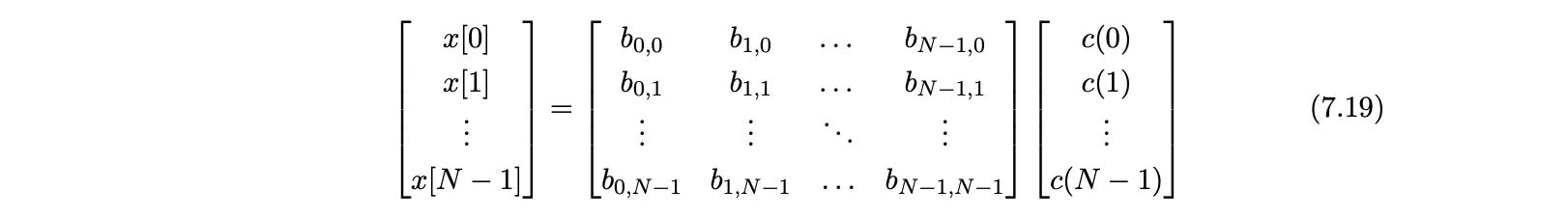
• x = B*c

in praktijk

• krijgen een set basis functies + input data → willen de coefficient waarden of gewichten c(k) krijgen

  

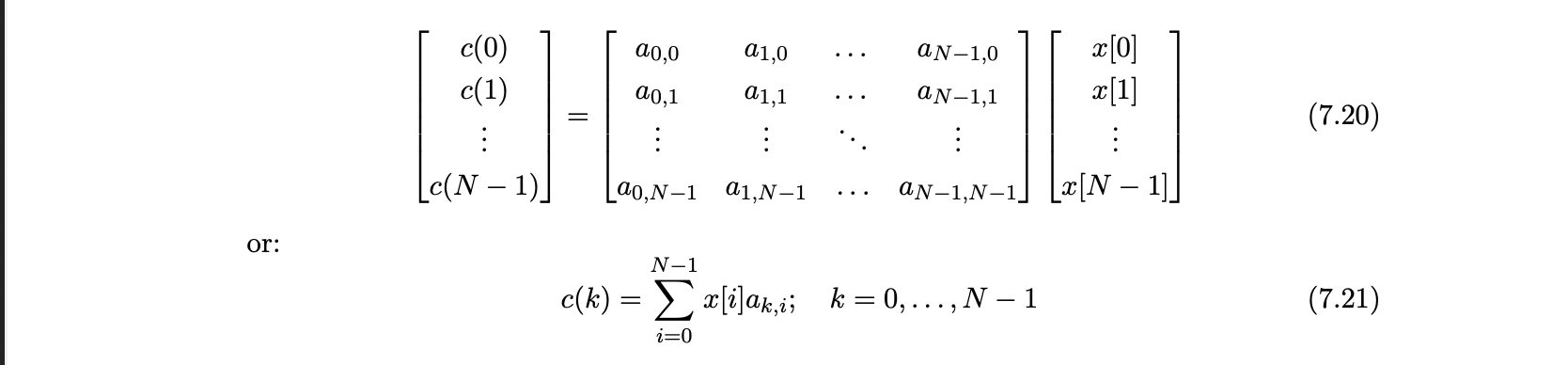
• c = A * c

  • x = A-1 * c

• B = A-1 * A → transformatie matrix

• c → transform coef

• kolommen van A-1 = basis functies van de transformaties

Unitary transform = orthogonaal + orthonormaal

• Basisfuncties zijn orthogonaal → inner product = 0.

  • onanfhankelijk en decorreleren het signaal

• orthonormaliteit: Basisfuncties hebben unit length (norm = 1).

• Mooie eigenschap: Aᵀ = A⁻¹ → c = A x en x = Aᵀ c.

  • Rijen van matrix A zijn de basisfuncties.

Andere belangrijke eigenschappen

• Totale energie van origineel en getransformeerd domein is gelijk.
   → inner product is preserved.

• Als je coëfficiënten verwijdert: de k grootste behouden minimaliseert de benaderingsfout (!).

• Autocorrelatiematrices in signaal- en transformdomein zijn gerelateerd:
  

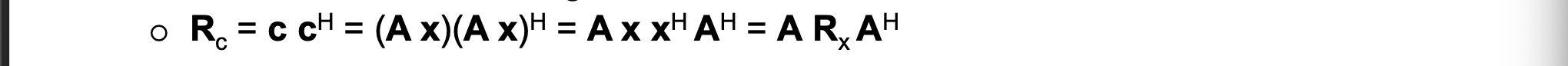
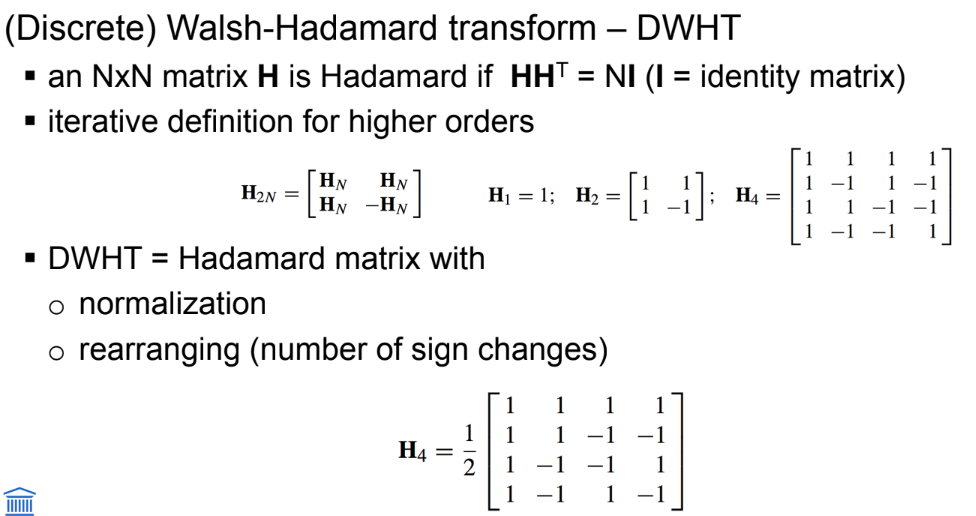
basic transforms: Walsh-Hadamard transform

De Walsh-Hadamard Transform (WHT) is een eenvoudige, lineaire en orthogonale transformatie die data omzet naar een andere representatie met enkel optellingen en aftrekkingen (geen vermenigvuldigingen nodig).

De Discrete WHT (DWHT) is de genormaliseerde versie ervan (delen door √N), zodat de matrix unitair wordt.

---

Toepassing:
Gebruikt in videocompressiesystemen zoals H.264/AVC (voor intra-frame coding).

Hoe werkt het?

• Gebaseerd op de Hadamard-matrix H, die opgebouwd wordt door herhaald splitsen:
    H₂ₙ = [ Hₙ Hₙ; Hₙ –Hₙ ]

• Basisfuncties worden gevormd door de rijen (na sequentievolgorde herschikking).

• Voorbeeld voor N = 4:
   H₄ =
   [1 1 1 1]
   [1 –1 1 –1]
   [1 1 –1 –1]
   [1 –1 –1 1]
  De DWHT normaliseert dit (delen door √N).

■ Waarom nuttig?

• Snel uit te voeren (geen vermenigvuldigingen).

• Energiecompactie: meeste energie zit in enkele coëfficiënten.

• Lage compressie-efficiëntie vergeleken met DCT, maar eenvoudiger.

the Karhunen-Loève Transform (KLT) (????)

The Karhunen-Loève transform is a reversible linear transform that exploits the statistical properties of the vector representation

• it optimally decorrelates the input signal

To understand the optimality of the KLT, consider the autocorrelation matrix Rx​ of the input vectors xi defined as

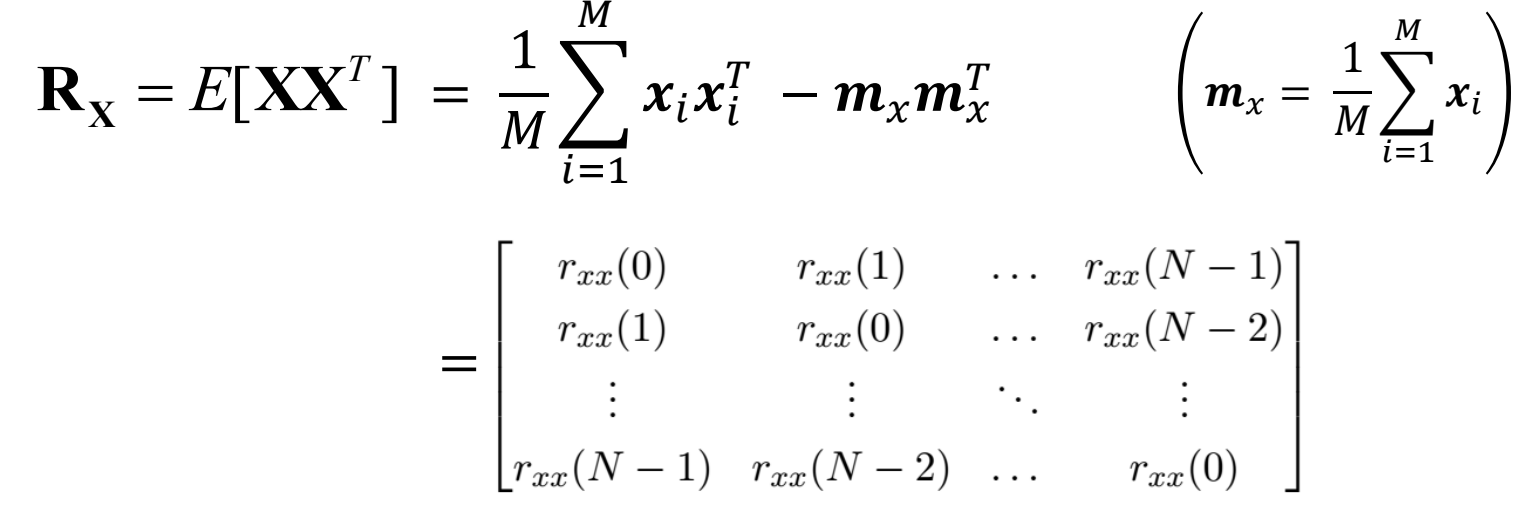
• Rx: symetrisch en niet negatief

  • N eigenvectoren a1, a2, a….

  • N eigen waarden lambda 1 ≥ lambda 2 ≥ …

Discrete Cosine Transform

■ Wat is DCT?
De Discrete Cosine Transform (DCT) is de meest gebruikte unitary transform voor beeld- en videocodering.

• lineaire orthonormale transformatie die een signaal omzet naar een representatie in termen van cos functies

• in tegenstelling tot KLT is DCT niet signaal afhankelijk

• decorrelatie: maakt de gegevens minder afh van elkaar

• energie compactie

■ Belangrijke eigenschappen:

• Zoals Fourier geeft DCT frequentie-informatie over een signaal, maar:
   ○ DCT werkt met reële waarden
   ○ DCT introduceert geen artefacten door periodieke extensie van het signaal

• DCT werkt uitzonderlijk goed voor signaalcompressie

• DCT heeft zeer goede energy compaction (energieconcentratie), en komt dicht bij de prestaties van de KLT voor gecorreleerde beelddata
   ○ zonder dat je de transform basisfuncties expliciet moet meezenden

■ Hoe werkt DCT?
De DCT van een signaal x[n] kan worden afgeleid door de DFT toe te passen op het symmetrisch uitgebreide (gespiegelde) signaal x1[n].

• Deze even extensie zorgt ervoor dat de imaginaire component (de sinusdelen) van de DFT wegvalt.

basisfuncties: zijn de kolomvectoren ven de inversie transformatie (reeel orthonormaal systeem zijn dit dezelfde als de rijen van de forward matrix)

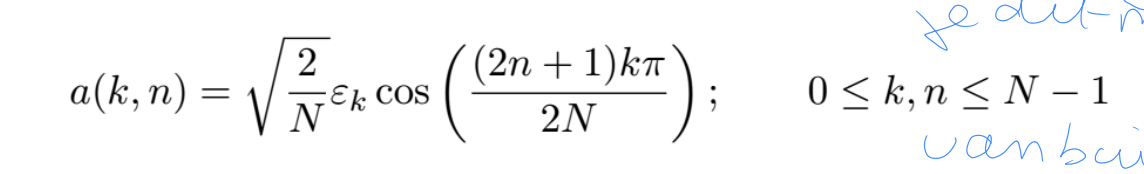
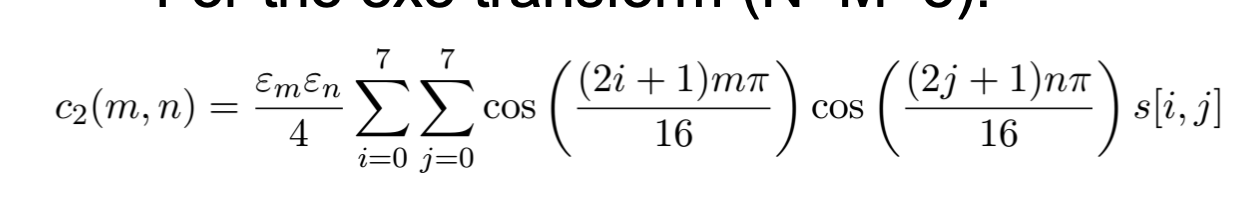
extension naar 2D

2D DCT = uitbreiding van 1D DCT, berekend als rijen + kolommen (separable → efficiënt).

Basisfuncties = outer product van 1D basisfuncties.

Groot voordeel: sterke energiecompactie, minder berekeningen.

Gebruikt in compressie (bv. JPEG) om data te reduceren met weinig kwaliteitsverlies.

Voorbeeld laat zien: met DCT en inverse DCT kan origineel blok exact hersteld worden (bij lossless).

Quantization of DCT coefficients

De DCT zelf zorgt niet voor compressie.

• Wat doet het wél?
  DCT concentreert energie in enkele grote coëfficiënten.

  • belangrijke coëfficiënten behouden (geen of weinig quantisatie),

  • minder belangrijke coëfficiënten grover quantiseren,

  • kleine coëfficiënten zelfs volledig verwijderen (op nul zetten).

• waarom

  • de transformatie decorrelatie oplevert

    • coef lijken op onafhankelijk getrokken

      • waarden → eenvoudige uniform quantizers

    • coef-weighted quantization

      • mensen minder gevoelig voor sommige freq → hiernaar quantiseren

• Use of coefficient-dependent weighting of the quantizer step-size

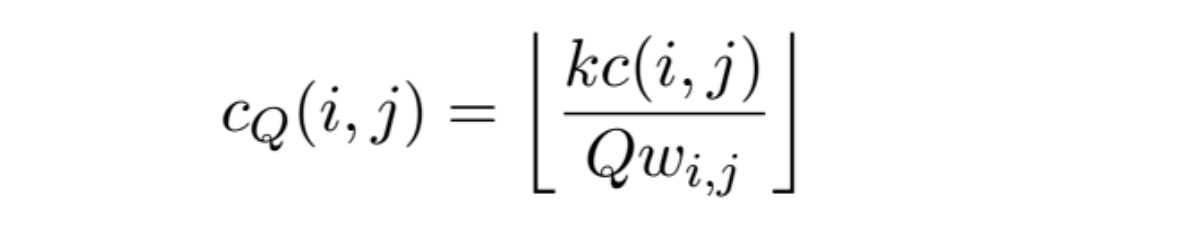
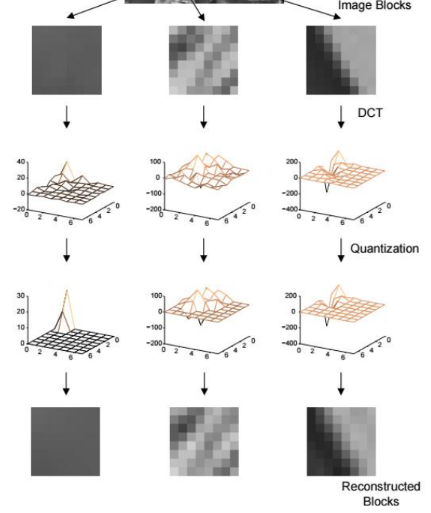
figuur:

• blokken met weinig strucutuur → minder coef nodig voor goeie reconstructie

• getextureerde blokken → meer coef nodig voor acceptabele kwaliteit

DCT implementation

Trade-off tussen decorrelatieprestatie en complexiteit:

• Decorrelatieprestatie hangt af van:

  • de grootte van de transformatie

  • autocorrelatiekenmerken van de data

    • inhoud

    • resolutie

    • enz

• Typisch gekozen blokgroottes: tussen 4×4 en 16×16

• JPEG gebruikt blokken van 8×8

Opmerking:

• Er bestaan efficiënte implementaties om de DCT-complexiteit te verminderen.

Kort: grotere blokken geven vaak betere decorrelatie maar kosten meer rekenwerk → je moet dus afwegen.