Investments - Formulas

Expected return - E[r]

Excel: =SUMPRODUCT(p_range; r_range)

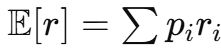
Variance - σ²

Excel: =SUMPRODUCT(p; r²) - (SUMPRODUCT(p; r))²

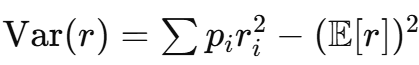
Standard deviation from variance - σ

=SQRT(variance_cell)

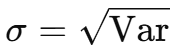
Covariance

Excel: =COVARIANCE.S(rA_range; rM_range)

Correlation (sample, time series)

Excel: =CORREL(rA; rB)

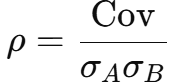
Mean vs geometric mean

Arithmetic: =AVERAGE(r); Geometric for periodic simple returns: =PRODUCT(1+r)^(1/n)-1

Sharpe Ratio

Excel: =(E[r]-rf)/sigma

Implied rfr_frf​ from Sharpe and (μ, σ)

r_f​ = μ − S σ

Normal VaR at 95% (returns)

Excel: =mu + NORM.S.INV(0.05)*sigma

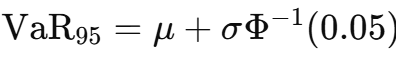
Normal ES at 95%

Excel: =mu - sigma*NORM.S.DIST(NORM.S.INV(0.05);FALSE)/0.05

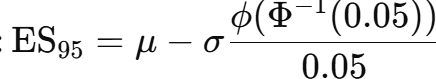
Historical VaR at q

Excel: =PERCENTILE.EXC(r; q)

Interpreting VaR number

95% VaR of −12%: on a typical day you lose ≤ 12%; 5% chance you lose more

Interpreting ES number

Average loss conditional on being in worst 5% outcomes

Gordon with next dividend D₁

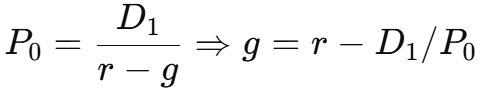
Gordon when given D₀

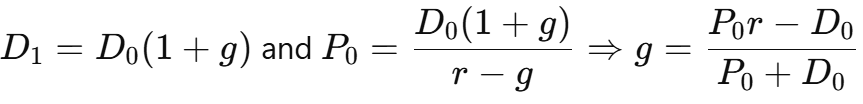
Multi-stage DDM — structure

PV of each stage’s dividends + terminal

Excel — PV of years 1–5 constant D1_5

=SUM(D1_5/(1+r)^{SEQUENCE(5)})

Terminal value at T with perpetual growth g

TV_T = CF_{T+1}/(r-g)

Multi-stage DDM (years 1–5 = D1₅; 6–10 = D6₁₀; then g)

• Stage 1 annuity PV: =PV(r; 5; D1_5; 0; 0)

• Stage 2 annuity PV at t=5: =PV(r; 5; D6_10; 0; 0) then PV today: =PV(r; 5; 0; -that; 0)

• TV at t=10: =D6_10*(1+g)/(r-g) then PV today: =PV(r; 10; 0; -TV; 0)

• Fair price = sum of three PVs

DDM when given D0

D1 = D0*(1+g); P0 = D1/(r-g). Solve g: = (P0*r - D0)/(P0 + D0)

HPR with dividends and split

=(P1*Shares*Split + Shares*Div - Shares*P0)/(Shares*P0)