Managerial Economics Ch. 1, 2, 18

Managerial differs from microeconomics

• Microeconomics focuses on description.

• Managerial economics is prescriptive

Managerial economics is an integrative course

• Brings the various functional areas of business together in a single analytical framework

Managerial economics exhibits economies of scope

• Integrates material from other disciplines

• Reinforces and enhances understanding of those

subjects

Managerial Objective

• Make choices that increase the value of the firm.

• The value of the firm is defined as the present value of

future profits.

Present value of expected future profits; equation

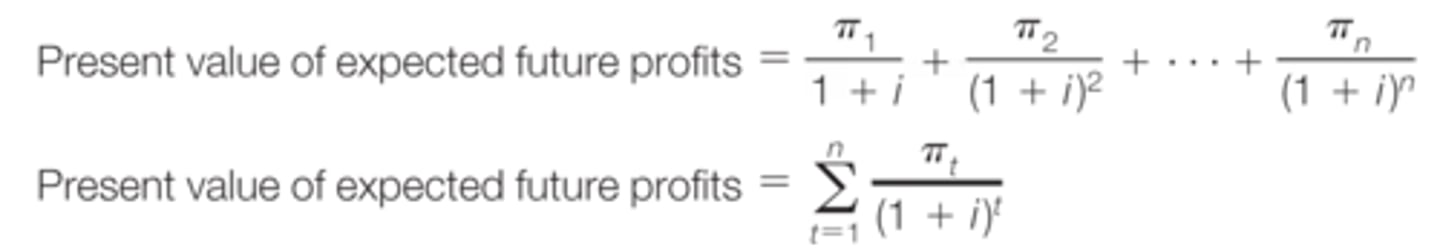
Managerial Choices

• Influence total revenue by managing demand

• Influence total cost by managing production

• Influence the relevant interest rate by managing

finances and risk

Managerial Constraints

• Available technologies

• Resource scarcity

• Legal or contractual limitations

Two Measures of Profit

Economic and Accounting Profit

Accounting Profit

• Historical costs

• Legal compliance

• Reporting requirements

Economic Profit

• Market value

• Opportunity, or implicit cost

• More useful measure for managerial decision making

PROFIT

• Measures the quality of managers' decision-making skills

• Encourages good management decisions by linkage with

incentives

SOURCES OF PROFIT

Innovation, Risk Taking, Exploiting Market Inefficiencies

Managerial Interests and the Principal-Agent Problem

The interests of a firm's owners and those of its managers may differ, unless the manager is the owner

Moral hazard

exists when people behave

differently when they are not subject to the risks

associated with their behavior.

• Managers who do not maximize the value of the firm may do so because they do not suffer as a

result of their behavior.

SOLUTION: MORAL HAZARD

Devise methods that lead to convergence of the interests of the firm's owners and its managers

Elasticity

Measures the percentage change in one factor given a small (marginal) percentage change in

another factor

Demand elasticity

Measures the percentage change in quantity demanded given a small (marginal) percentage change in another factor that is related to demand

role of managers in controlling and predicting market demand

• Managers can influence demand by controlling price, advertising, product quality, and distribution strategies.

• Managers cannot control, but need to understand,

elements of the competitive environment that

influence demand

• Managers cannot control, but need to understand

how the macroeconomic environment influences

demand

Determinants of the position and shape of the

market demand curve

1. Consumer tastes

2. Consumer income

3. Population size in the market

normal good

a good that consumers demand more of when their incomes increase

inferior good

a good that consumers demand less of when their incomes increase

parameter

Constant or variable terms used in

the function that helps managers determine the specific form of the function but not its general

nature

Relationship between the market demand function and market demand curve

• Market demand curve shows the relationship between Q and P when all other variables are held constant at specific values.

• Market demand function does not explicitly hold any values constant.

Own-price elasticity of demand

The elasticity of a function is the percentage change

in the dependent (Y) variable in response to a 1

percent increase in the independent (X) variable

price elasticity of a demand function

the percentage change in quantity demanded in response

to a 1 percent increase in price.

own price elasticity of demand formula

Price Elasticity=(P/Q)(%change in Q/%change in P)

0 n -∞

• When |n| > 1, demand is elastic.

• When |n| < 1, demand is inelastic.

• When |n| = 1, demand is unitary.

price inelastic

Buyers are not sensitive to price changes and demand is relatively unchanged.

price elastic

Consumers are very sensitive to price changes and buy more at low prices and less at high prices.

Demand is perfectly inelastic

Quantity demanded is the same at all prices

demand is perfectly elastic

• Price is the same for all quantities demanded.

• If price rises, quantity demanded falls to zero.

• If price falls, quantity demanded increases without limit.

At the midpoint of a linear demand curve...

= -1, with n

approaching zero as price approaches zero.

• At prices above the midpoint, demand is elastic, with n

approaching negative infinity as quantity approaches zero.

• At prices below the midpoint, demand is inelastic.

point price elasticity

A measure of the elasticity of demand at a particular point on the demand curve.

- should be used working with an estimated demand curve or when the change in price is very small

arc midpoints formula

Example: P1 = 5, P2 = 4, Q1 = 3, and Q2 = 40

• n = [(40 - 3)/(4 - 5)][5/3] = -61.67 (when price falls)

• n = [(3 - 40)/(5 - 4)][4/40] = -3.70 (when price rises)

If n > -1 (inelastic), dTR/dP> 0, so an increase in P

will increase total

revenue

If n < -1 (elastic), dTR/dP< 0, so an increase in P

will decrease total revenue.

marginal revenue formula

P(1 + 1/n)

Income elasticity of demand

the percentage change in quantity demanded (Q) resulting from

a 1% change in consumers' income (I)

Income elasticity of demand formula

(% change in quantity demanded / % change in income)(Income/quantity)

Income elasticity of demand >0

Normal Good

Income elasticity of demand < 0

inferior good

Cross-price elasticity of demand (nxy)

the percentage change in quantity demanded of one

good (QX) resulting from a 1% change in the

price of a related good (PY)

nxy > 0

substitutes

nxy < 0

complements

nxy formula

(half derivative Qx/half derivative Py)(Py/Qx)

Constant-elasticity demand function:

Mathematical form that always yields that same

elasticity, regardless of the product's price and

consumers' income

Difference Rule

dY/dX = dU/dX - dW/dX

Sum Rule

dY/dX = dU/dX + dW/dX

Product Rule

dY/dX = UdW/dX + WdU/dX

Quotient Rule

dY/dX = [W(dU/dX) -U(dW/dX)]/W2

Chain Rule

dY/dX = (dY/dW)(dW/dX)

For maximum, dY/dX = 0

d2Y/dX2 <0

For minimum, dY/dX = 0

d2Y/dX2>0