EOT exam 2000psy
0.0(0)
Card Sorting
1/101
There's no tags or description
Looks like no tags are added yet.
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
102 Terms
1
New cards
What is another name for a Repeated Measures Design?
Within Subjects Design
2
New cards
What are the threats of validity in a repeated measures design ?
Practice effects order effects and fatigue effects
3
New cards
What might we expect of POWER in a repeated-measures design - assuming all other things equal?
Power will increase
4
New cards
What method can be used to overcome order effects in repeated-measures designs?
Counterbalancing
5
New cards
Power is enhanced by a repeated measures design because
Reduced variability due to individual differences
Less random error due to more observations per participant
Less random error due to more observations per participant
6
New cards
Which experimental design would be used for testing a longitudinal seqeunce based research design?
Related samples
7
New cards
How many participants does a repeated mesures design need compared to a between subjects design?
Less participants are needed for the same level of power
8
New cards
Sensitisation effects occur when:
A participant finds out why the researcher is doing the study
9
New cards
A match design analyses data as if it was _____ type of design?
A repeated measures design
10
New cards
What is a disadvantage of using a matched pairs design?
Matching is difficult, time and energy and participants may guess the purpose of the experiment.
11
New cards
Describe a between- subjects design ?
Between-subjects manipulations are where different groups of people provide data in each experimental condition. Scores on the DV come from different samples that are unrelated to one another. Between-subjects designs are otherwise called unrelated samples, independent-samples, uncorrelated samples/measures, between-participants, or between groups.
12
New cards
What are the disadvantages of a between-subjects design?
One major disadvantage is the problem of Individual differences . A good experimental design needs to rule out systematic bias stemming from individual differences between participants across experimental groups. If these individual differences cannot be ruled out completely, then they should at least be relatively even across experimental conditions (using random assignment to conditions is the best way to minimise the effects of individual differences in a between-subjects design). Another limitation is that logistically and practically we generally we need a lot more participants for a between-groups design.
13
New cards
What is a within-subjects design?
Within-subjects designs involve the repeated collection of data from the same participants. In these designs, the same group of participants perform the task or provide data in all experimental conditions. Within-subjects designs are otherwise called related samples, dependent-samples/measures, correlated-samples/measures, repeated-measures, within-participants, within-groups.
14
New cards
What are the advantages of a within-subjects design?
Repeated-measures manipulations are generally
preferable to between-subjects designs. One major advantage is reducing the background variation against which we assess the impact of the IV on the DV. Within-subjects designs eliminate permanent or chronic Individual differences (each individual carries over individual differences into each new condition). \n Fewer participants are also required for a within-subjects design because the same group of participants can provide data under multiple experimental conditions.
preferable to between-subjects designs. One major advantage is reducing the background variation against which we assess the impact of the IV on the DV. Within-subjects designs eliminate permanent or chronic Individual differences (each individual carries over individual differences into each new condition). \n Fewer participants are also required for a within-subjects design because the same group of participants can provide data under multiple experimental conditions.
15
New cards
What are the disadvantages of a within-subjects design?
A major disadvantage of the within-subjects design is order effects . When we collect repeated measurements from the same individuals we are introducing a Confounding variable arising from the **order** in which we present the experimental conditions. Order effects can Improve scores (i.e., through practice and familiarity) and they can be detrimental to scores (i.e., through a decline in concentration and increased fatigue).
Another disadvantage is carry-over effects (otherwise called sequencing effects). These effects occur when one **sequence of conditions** (i.e., if condition A is completed first and then condition B) can lead participants to be more or less fatigued, **bored** or practiced than an alternative sequence (i.e., if condition B is completed first and then condition A). Sometimes carry-over effects are temporary for example if we complete a cognitively effortful task we might feel temporarily depleted but these resources will replenish after a short rest. However, sometimes carry-over effects are **permanent** – for example if we learn a new way of completing a task through following a set of experimental instructions in condition A. We cannot then unlearn or forget that strategy when completing the task again in condition B.
Another disadvantage is carry-over effects (otherwise called sequencing effects). These effects occur when one **sequence of conditions** (i.e., if condition A is completed first and then condition B) can lead participants to be more or less fatigued, **bored** or practiced than an alternative sequence (i.e., if condition B is completed first and then condition A). Sometimes carry-over effects are temporary for example if we complete a cognitively effortful task we might feel temporarily depleted but these resources will replenish after a short rest. However, sometimes carry-over effects are **permanent** – for example if we learn a new way of completing a task through following a set of experimental instructions in condition A. We cannot then unlearn or forget that strategy when completing the task again in condition B.
16
New cards
What are 2 methods that can be used to overcome order effects in repeated-measures designs?
Counterbalancing is the best option and this involves ensuring that each condition in an experiment follows, and is preceded by, every other condition an equal number of times. Randomisation is the next best option and this involves randomising the order of the experimental conditions (this is less preferred than counterbalancing because it does not always result in equal sample sizes across experimental conditions).
17
New cards
We could provide extensive practice and warm-up before commencing the experimental tasks themselves. We could also introduce a gap between conditions so that participants can replenish their resources (i.e., return to baseline before completing the next task).
18
New cards
What is a strategy we can use to minimise the effects of a permanent carry-over (practice) effect?
There is not much we can do about permanent carry-over effects. The best thing would be to use a between-subjects design instead.
19
New cards
What are the 3 procedural steps involved in creating a matched design?
• Measure participants on known variables to affect the DV
• Match participants on these key variables (create equivalent pairs)
• Randomly assign matched participants to experimental groups
• Match participants on these key variables (create equivalent pairs)
• Randomly assign matched participants to experimental groups
20
New cards
What analysis should we use to analyse the data collected using a matched design?
When using a matched design we would analyse the data as though it is repeated measures not an independent samples . What this means is that the data is organised as though each matched pair is a single participant, not a different participant.
21
New cards
What are the advantages of a matched design?
Matched designs can Increase statistical power depending on the effectiveness of matching procedure or how effective individual differences have been accounted for. This is an advantage of the matched pairs design over between subjects, it can more effectively eliminate the effect of individual differences compared to using randomisation of participants in a between-subjects design.
Matched designs also do not lead to this is an advantage over the within-subjects design
A third advantage is that a matched design can improve internal and external validity. By controlling for individual differences and ensuring equivalence across groups on important variables – this makes conclusions regarding cause-and-effect more convincing (i.e., improves internal validity). By allowing anyone in the study as long as they have a matched pair on the important variables, then the sample can also be more representative of real people (i.e., improves external validity). Again, this depends though on the effectiveness of the matching procedure.
Matched designs also do not lead to this is an advantage over the within-subjects design
A third advantage is that a matched design can improve internal and external validity. By controlling for individual differences and ensuring equivalence across groups on important variables – this makes conclusions regarding cause-and-effect more convincing (i.e., improves internal validity). By allowing anyone in the study as long as they have a matched pair on the important variables, then the sample can also be more representative of real people (i.e., improves external validity). Again, this depends though on the effectiveness of the matching procedure.
22
New cards
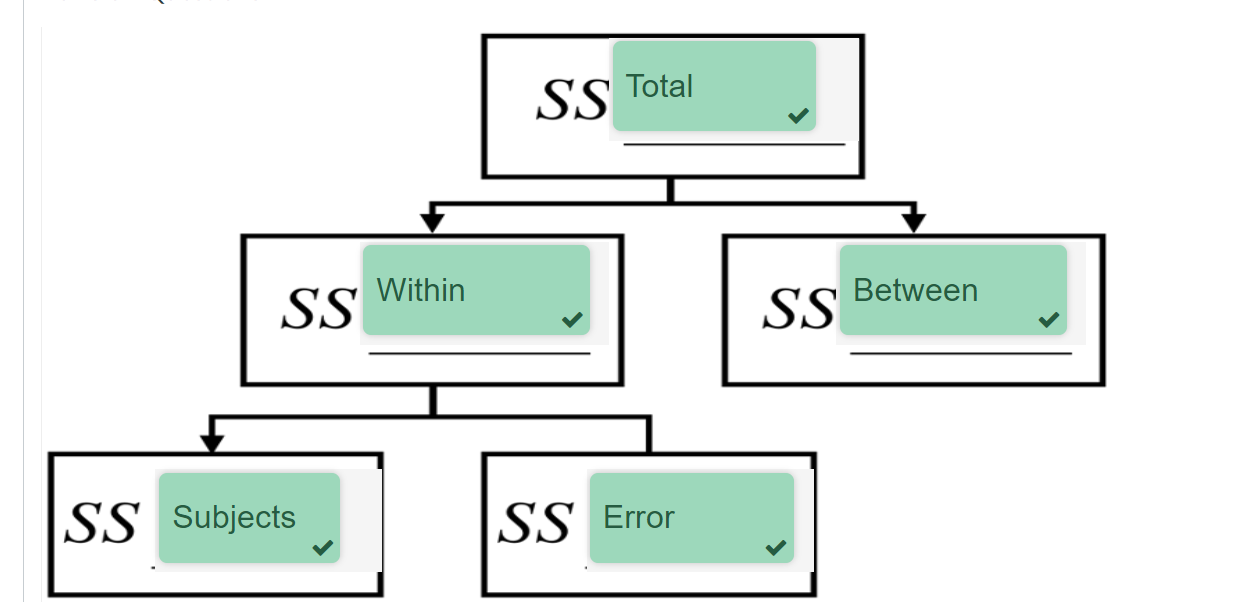
Diagram for partitioning of variance ONE- WAY within subjects ANOVA
23
New cards
The F-ratio for the one-way within-subjects ANOVA uses a ratio of which two Sums of Squares?
MS BETWEEN/ MS ERROR
24
New cards
In a one-way within-subjects ANOVA, what does the SS total measure?
The SS total measures total variation in scores on the DV. It is calculated as the difference between each observed data point and the grand mean across all experimental conditions.
25
New cards
In a one-way within-subjects ANOVA, what does the SS between represent?
the SS between measures variation due to the intervention, or the difference between condition means or what we sometimes call effect variance. It is calculated as the difference between each participants predicted value (or the conditioned mean) and the grand mean.
26
New cards
In a one-way within-subjects ANOVA, what does the SS subject represent?
The SS subject represents variation due to individual differences (within participants that is due to individual differences) this is calculated using the difference between the mean for each subject (or participant) across all experimental conditions and the grand mean
27
New cards
In a one-way within-subjects ANOVA, what does the SS error represent?
The SS Error represents variation in DV scores due to random error or **measurement error**. The SS error is the remaining **within-participant variation** (not **between-subjects variance**) that is not due to individual differences (i.e., is not part of the **SS subject**) but is due to measurement error
28
New cards
Why do we use the Mean Squares values rather than the Sum of Squares values to calculate the F-ratio in a one-way within-subjects ANOVA?
Mean Squares are calculated to: eliminate the bias associated with the number of scores used to calculate the sum of squares
Because the SS calculations are based on summed values, they are influenced by the number of scores that were summed ( eg the more numbers by the degrees of freedom) to standardize these ss values and make the comparable
.This average SS is what we call the MS
Because the SS calculations are based on summed values, they are influenced by the number of scores that were summed ( eg the more numbers by the degrees of freedom) to standardize these ss values and make the comparable
.This average SS is what we call the MS
29
New cards
In a research scenario where 60 participants provided data on 3 separate occasions, what are the values for the different degrees of freedom below ?
Use this formula to help you:
* df total = N - 1
* df between = k – 1
* df within = N - k
* df subjects = n - 1
* df error = df within - df subjects
Use this formula to help you:
* df total = N - 1
* df between = k – 1
* df within = N - k
* df subjects = n - 1
* df error = df within - df subjects

30
New cards
Using the above calculations, when reporting the F-ratio for a one-way within- subjects ANOVA, what Degrees of Freedom values should be inserted inside the brackets (i.e., *F*(?, ?) = 116.47) if *F*(df between, df error) = 116.47
F ( 2 ), (118 ) = 116.47
31
New cards
The value for SS within is not used in the calculation of the F-ratio in the one-way repeated-measures ANOVA. True or False?
TRUE
32
New cards
The SS subjects calculated is used in the F-ratio calculation for the one-way between-subjects ANOVA. True or False?
FALSE
33
New cards
What formula is used to calculate the F-ratio for the one-way repeated-measures ANOVA?
F = MS between/MS error
34
New cards
With a main effect for a one-way repeated-measures ANOVA of *F*(4, 89) = .82, this F-ratio likely to be statistically significant. true or false ?
False
It is likely to be not significant. An F-ratio less than 1 tells us that there is more error variance than effect variance in the data. This means the effect will not be statistically significant. An F-ratio close to 1 (or less than 1) tells us there is unlikely to be an effect in the data because the effect variance is not substantially larger than the error variance.
It is likely to be not significant. An F-ratio less than 1 tells us that there is more error variance than effect variance in the data. This means the effect will not be statistically significant. An F-ratio close to 1 (or less than 1) tells us there is unlikely to be an effect in the data because the effect variance is not substantially larger than the error variance.
35
New cards
In a repeated-measures design with 1 independent variable with 4 conditions, equal numbers of participants in each condition, and 40 total scores, how many participants were involved in the study?
**Answer = 10. Because 40 total scores divided by 4 conditions = 10 scores per condition (i.e., 10 participants per condition).**
36
New cards
In a repeated-measures design with 1 independent variable and 36 scores in each of 3 conditions, how many participants were involved in the study?
Answer = 36. If there are 36 scores in all 3 conditions, this means there must be 36 individual participants. The total number of scores across all conditions would be 108 (36\*3) but the 36 participants each contribute 3 different scores to that total.
37
New cards
If there are 32 participants in a study, and they provide data on 3 occasions, how many total scores in our data file?
Answer = 96. The total number of scores is calculated by multiplying the number of participants (32) and the number of conditions (3)
38
New cards
If there are 5 repeated-measures experimental conditions, with 15 scores in each condition, how many participants were involved in the study?
Answer = 15. If there are 15 scores in all 5 conditions, this means there must be 15 individual participants. The total number of scores across all conditions would be 75 (15\*5) but the 15 participants each contribute 5 different scores to that total.
39
New cards
What are the assumptions of the one-way within-subjects ANOVA?
Level of measurement: The DV must be measured at the **interval or ratio scale** This is met by the **study design.**
Random sampling: Scores must be obtained using a **random sample This is met by the study design.**
Normal distribution: The distribution of scores on the DV across all groups in the analysis should be normal. This is met by statistically testing the data
\
Random sampling: Scores must be obtained using a **random sample This is met by the study design.**
Normal distribution: The distribution of scores on the DV across all groups in the analysis should be normal. This is met by statistically testing the data
\
40
New cards
What is a Bonferroni correction?
A manual Bonferroni adjustment involves running our comparisons with no embedded or automatic adjustment for type 1 error rate. We handle the potential inflation of type 1 error rate by manually altering the alpha level we use to determine statistical significance. We create the new alpha level by dividing the original alpha level (p < .05) by the number of tests or number of comparisons conducted. For example, if we have 3 experimental groups (2 treatment groups and a control group) and we compare each experimental group against the control (treatment 1 vs control; treatment 2 vs control) we would use an adjusted alpha of p < .025 (.05/2) to judge statistical significance. If we compare each experimental group against each other experimental group (treatment 1 vs control; treatment 2 vs control; treatment 1 vs treatment 2) we would use an adjusted alpha of p < .016 (.05/3) to judge statistical significance.
41
New cards
When would we use a Bonferroni correction?
We would use a Bonferroni correction when we run follow-up tests to explore a significant main effect But specifically, we would use a Bonferroni adjustment when those follow-up tests are non-orthogonal (i.e., involve using the same experimental condition or chunk of variance in multiple comparisons) and if we have not used a statistical test that makes an automatic adjustment for type 1 error rate (i.e., **Tukey’s HSD**). You only need to use one approach or the other to control for **type 1 error inflation** there is no need to use a Bonferroni adjustment and Tukey’s HSD posthoc tests (this is doubling up).
42
New cards
If we run a one-way within-subjects ANOVA with 4 conditions and we conduct posthoc tests comparing each experimental condition with each other experimental condition, what would the adjusted alpha be if we used a Bonferroni correction to adjust for type 1 error rate?
*p* < .008
With 4 conditions and pairwise comparisons comparing all conditions, there would be 6 comparisons in total (1 v 2; 1 v 3; 1 v 4; 2 v 3; 2 v 4; 3 v 4). This means we would use an adjusted cut-off of *p* < .008 for significance (.05/6). So rather than the usual *p* < .05 cut-off, our individual comparisons would need to have an associated p-value of less than .008 to be able to conclude that these differences were statistically significant
With 4 conditions and pairwise comparisons comparing all conditions, there would be 6 comparisons in total (1 v 2; 1 v 3; 1 v 4; 2 v 3; 2 v 4; 3 v 4). This means we would use an adjusted cut-off of *p* < .008 for significance (.05/6). So rather than the usual *p* < .05 cut-off, our individual comparisons would need to have an associated p-value of less than .008 to be able to conclude that these differences were statistically significant
43
New cards
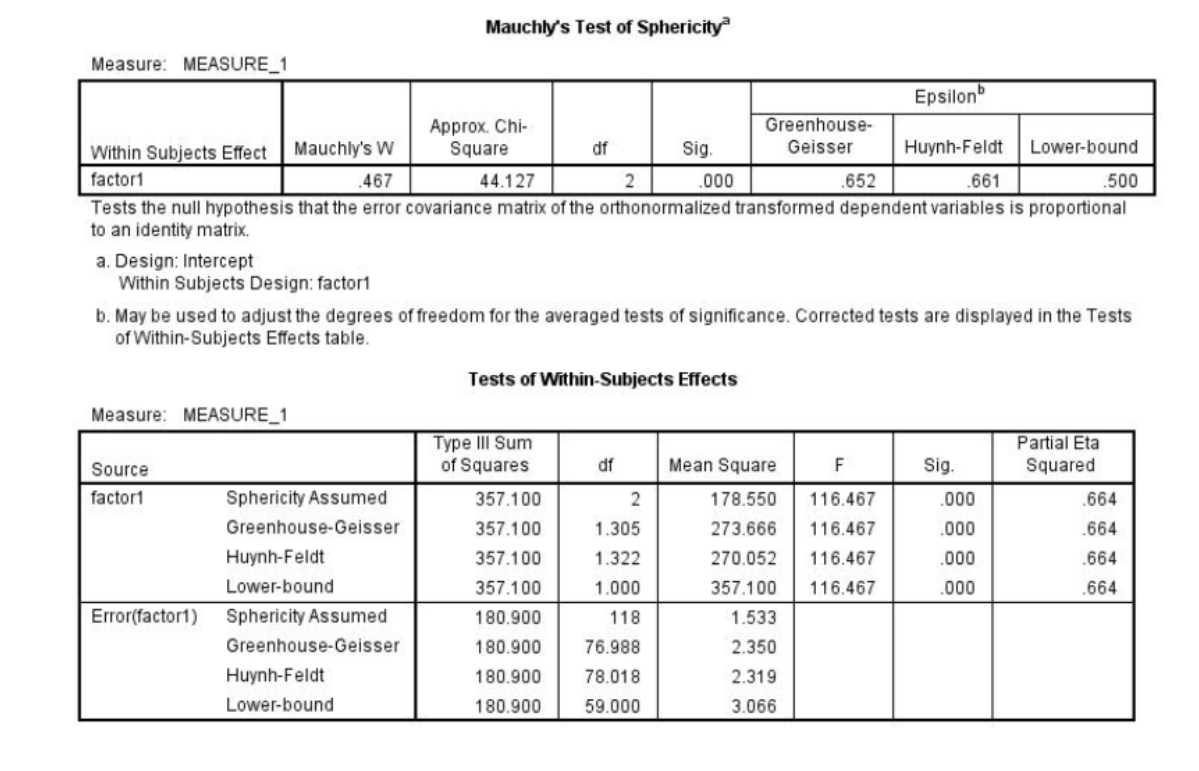
In the output below for a one-way within-subjects ANOVA with 3 experimental conditions, answer the following questions
What assumption does Mauchly’s test for?
Has the assumption of sphericity been violated?
How do you know?
What is the p value for Mauchley's?
What is the greenhouse-geisser correction factor?
Is there a significant main effect for Factor 1?
What assumption does Mauchly’s test for?
Has the assumption of sphericity been violated?
How do you know?
What is the p value for Mauchley's?
What is the greenhouse-geisser correction factor?
Is there a significant main effect for Factor 1?
1. sphericity
2. yes
3. Mauchlys test is significant
4. P< .001
5. .652
6. yes
44
New cards
How would you report the main effect for the above SPSS output in a format you would see in a Results section of a laboratory report?
There was a large significant main effect, F (1.31, 76.99) = 116.47, p < .001, partial η2 = .66. \[ Don’t forget that when the sphericity assumption is violated (i.e., Mauchly’s test is statistically significant), the greenhouse-geisser adjusted values for degrees of freedom should be reported. \]
45
New cards
Is Between subjects with 1 IV and 3 DVs a factorial design ?
No
Correct. Because this option has 3 dependent variables. None of the factorial ANOVAs test more than 1 DV simultaneously. But a factorial ANOVA can test 3 or more IVs simultaneously.
Correct. Because this option has 3 dependent variables. None of the factorial ANOVAs test more than 1 DV simultaneously. But a factorial ANOVA can test 3 or more IVs simultaneously.
46
New cards
What is an example of a factorial design with 4 independent varivariables?
* 2 x 2 x 3 x 4
As the number of IVs is represented by the number of values in the design statement, this is the correct answer.
As the number of IVs is represented by the number of values in the design statement, this is the correct answer.
47
New cards
What is an example of a within-subjects factorial design ?
2 x 2: task (with blindfold, without) and time (pre, post)
Correct as participants can be in both conditions of each variable. Meaning, the participants will participate in all conditions of the two IVs
Correct as participants can be in both conditions of each variable. Meaning, the participants will participate in all conditions of the two IVs
48
New cards
How many cells are there in a 2 x 2 x 3 design?
12
Correct because 2 x 2 = 4. Then 3 x 4 = 12.
Correct because 2 x 2 = 4. Then 3 x 4 = 12.
49
New cards
A between-subjects factorial ANOVA cannot be quasi-experimental true or false?
The answer is false because quasi-experimental research simply involves the manipulation of an independent variable without the random assignment of participants to conditions.
50
New cards
Factorial designs investigate the separate effects of all IVS true or false ?
True These are called main effects
51
New cards
A mixed factorial design is ?
When there are between and within subjects variables
A mixed design has independent variables that are both within and between in design. This is the defining factor of a mixed-design ANOVA
A mixed design has independent variables that are both within and between in design. This is the defining factor of a mixed-design ANOVA
52
New cards
A 2 ( does exercise, does not) x 2 (nonsmoker, smoker) between-subjects design interaction…
Looks at if exercise habit depends on smoking status
**Good, we can look at different smoking conditions and exerercise conditions to determine this.**
**Good, we can look at different smoking conditions and exerercise conditions to determine this.**
53
New cards
A researcher was interested in the effects of alcohol on self-reported enjoyment among young adults at a party. Ninety young adults were asked to recall a party they attended where they were sober and consumed no alcohol, a party where they had a few drinks, and a party where they were drunk. For each of the three party scenarios identified, they were asked to provide a rating of their enjoyment. Identify (drag and drop below) the requested factors (a,b,c,d,e) for this scenario:
Independent variable
levels
name of levels
main effects
design
dependent variable
analysis
\
Independent variable
levels
name of levels
main effects
design
dependent variable
analysis
\
1. alchohol consumption
2. 3
3. none, moderate, drunk
4. effect of alcohol
5. Within-subjects
6. enjoyment
7. One way within subjects anova
54
New cards
A researcher was interested in investigating the effects of experience and training task on efficiency in work performance. He collected data from 30 employees (10 novices, 10 intermediate and 10 advanced) and randomly allocated them to one of 2 training conditions: didactic or experiential. Identify (write below) the requested factors (a,b,c,d,e) for this scenario:
Independent variable
levels
name of levels
main effects
design
dependent variable
analysis
Independent variable
levels
name of levels
main effects
design
dependent variable
analysis
a. Independent variables – experience (3 levels: novice, intermediate, advanced) and training (2 levels: didactic, experiential)
i) 6 cells (3 x 2)
b. Main effects – 2 main effects (experience and training) and 1 interaction (experience x training)
c. Design – between-subjects
d. Dependent variable – work efficiency
e. Analysis – independent-measures factorial ANOVA
i) 6 cells (3 x 2)
b. Main effects – 2 main effects (experience and training) and 1 interaction (experience x training)
c. Design – between-subjects
d. Dependent variable – work efficiency
e. Analysis – independent-measures factorial ANOVA
55
New cards
A researcher was interested in investigating the effects of age and exercise on cognitive decline. She recruited a sample of 60 participants (30 in mid-late adulthood, and 30 elderly) and measured their cognitive performance at the beginning of the study and again 12 weeks later after having been participating in a structured exercise program. Identify (drag and drop below) the requested factors (a,b,c,d,e) for this scenario:
Independent variable
levels
name of levels
main effects
design
dependent variable
analysis
Independent variable
levels
name of levels
main effects
design
dependent variable
analysis
a) Independent variables – age (2 levels: adult, elderly) which is
between-subjects and time (2 levels: baseline, and 12-weeks) which is within-subjects
b) 4 cells (2 x 2)
c) Main effects – 2 main effects (age and time) and 1 interaction (age x time)
d) Design –mixed
e) Dependent variable – cognitive performance
f) Analysis – mixed factorial ANOVA
between-subjects and time (2 levels: baseline, and 12-weeks) which is within-subjects
b) 4 cells (2 x 2)
c) Main effects – 2 main effects (age and time) and 1 interaction (age x time)
d) Design –mixed
e) Dependent variable – cognitive performance
f) Analysis – mixed factorial ANOVA
56
New cards
A researcher was interested in investigating whether students study more effectively with a constant background sound, variable background sound, or no sound at all. Twenty-four participants were randomly allocated to one of the experimental conditions after which they were asked to study some material for 30 minutes. At the end of the study period, they completed a multiple choice test assessing their learning. Identify (fill in the missing words) the requested factors (a,b,c,d,e) for this scenario:
Independent variable
levels
name of levels
main effects
design
dependent variable
analysis
Independent variable
levels
name of levels
main effects
design
dependent variable
analysis
a. Independent variable – (3 levels: constant, variable, none)
b. Main effects – 1 main effect (main effect of sound)
c. Design – Between-subjects
d. Dependent variable – performance on multiple choice test
e. Analysis – one-way between-subjects
b. Main effects – 1 main effect (main effect of sound)
c. Design – Between-subjects
d. Dependent variable – performance on multiple choice test
e. Analysis – one-way between-subjects
57
New cards
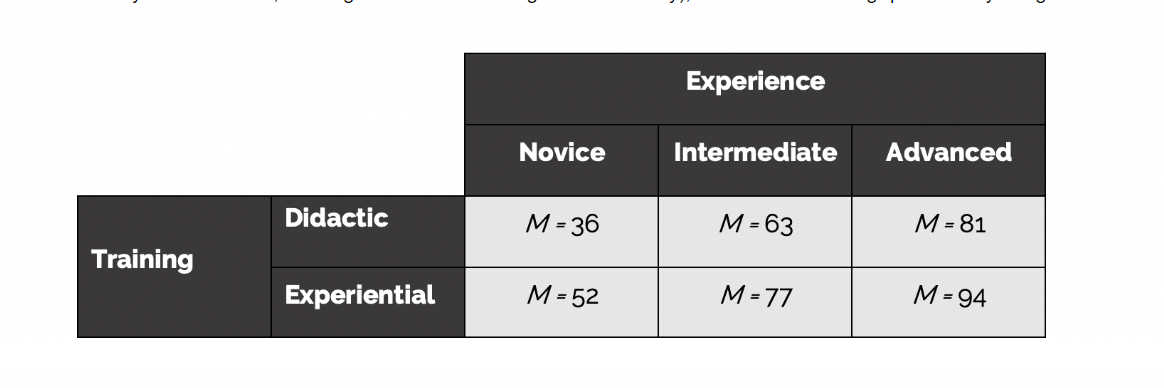
a. What is the mean efficiency for novices?
b. What is the mean efficiency for intermediate workers?
c. What is the mean efficiency for advanced workers?
d. What is the mean efficiency for the didactic training approach?
e. What is the mean efficiency for the experiential approach?
b. What is the mean efficiency for intermediate workers?
c. What is the mean efficiency for advanced workers?
d. What is the mean efficiency for the didactic training approach?
e. What is the mean efficiency for the experiential approach?
a. What is the mean efficiency for novices? **44**%
b. What is the mean efficiency for intermediate workers? **70**%
c. What is the mean efficiency for advanced workers? **87.5**%
d. What is the mean efficiency for the didactic training approach? **60**%
e. What is the mean efficiency for the experiential approach? **74.33**%
b. What is the mean efficiency for intermediate workers? **70**%
c. What is the mean efficiency for advanced workers? **87.5**%
d. What is the mean efficiency for the didactic training approach? **60**%
e. What is the mean efficiency for the experiential approach? **74.33**%
58
New cards
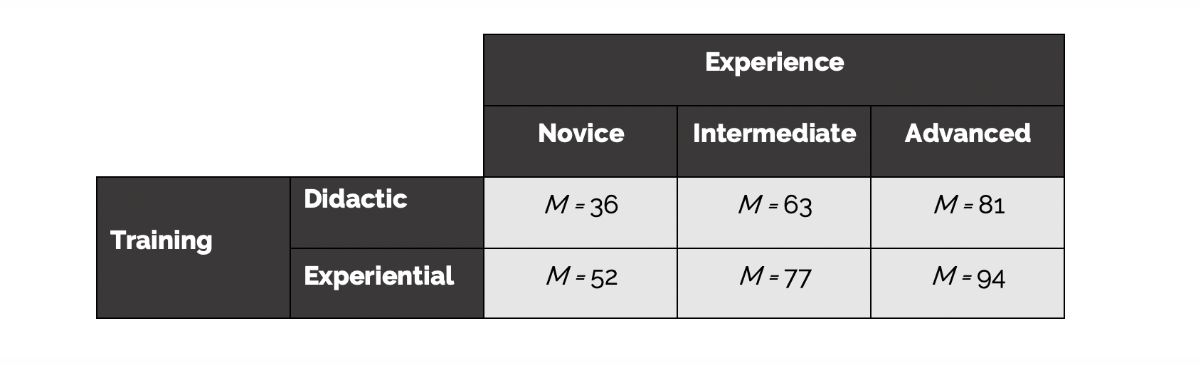
a. What is the mean efficiency for novices? **44**%
b. What is the mean efficiency for intermediate workers? **70**%
c. What is the mean efficiency for advanced workers? **87.5**%
d. What is the mean efficiency for the didactic training approach? **60**%
e. What is the mean efficiency for the experiential approach? **74.33**%
\
For the data in the table above, do you think there is a main effect for experience level? Explain why/why not
b. What is the mean efficiency for intermediate workers? **70**%
c. What is the mean efficiency for advanced workers? **87.5**%
d. What is the mean efficiency for the didactic training approach? **60**%
e. What is the mean efficiency for the experiential approach? **74.33**%
\
For the data in the table above, do you think there is a main effect for experience level? Explain why/why not
Yes. The efficiency level increases linearly (in a straight line upward) with greater experience.
59
New cards
For the data in the table above, do you think there is a main effect for training? Explain why/why not
Yes. The efficiency scores for the experiential approach are higher than for the didactic training approach.
60
New cards
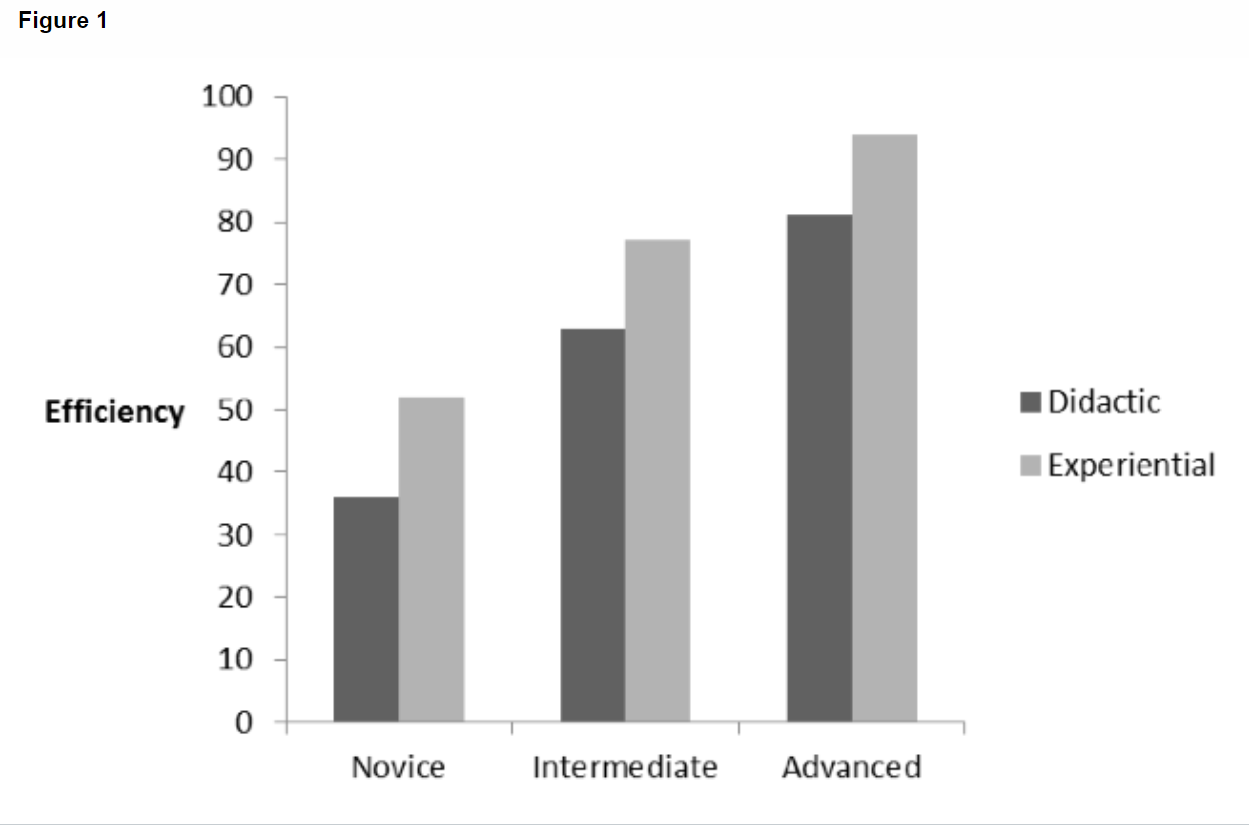
Looking at the plot of the means in the figure above, do you think there is an interaction between experience and training? Explain why/why not.
No. The effectiveness of the training approach does not appear to depend on level of experience. The experiential approach is better than the didactic approach for all workers regardless of experience. Furthermore, the advanced workers are more efficient than the intermediate workers, and the intermediate workers are more efficient than the novices, regardless of training approach. The pattern of results would therefore indicate two main effects but no interaction.
61
New cards
Factorial designs are useful because they provide:
* A main effect for each independent variable in isolation
* An interaction effect (effect of the IVs in combination)
* An interaction effect (effect of the IVs in combination)
62
New cards
In a factorial between groups ANOVA, each participant appears:
In only one experimental condition
63
New cards
Which of the following assumptions should be met before a factorial between groups ANOVA?
* Normality
* Homogeneity of Variance
* Homogeneity of Variance
64
New cards
A 2 x 3 between-subjects design, means that:
* There are three levels of the second independent variable
* There are two independent variables
* There are two independent variables
65
New cards
How many dependent variables are there in a two-way ANOVA?
1 Correct, a two-way ANOVA can only have one DV. To be able to test more than one DV, we would need to use a fancy test called a MANOVA. But don't worry about this test, this is something we cover in later years.
66
New cards
What does partial eta squared tell us?
How much variance in the DV accounted for by the IV
Correct as partial eta sqaured is the effect size for factorial ANOVA.
Correct as partial eta sqaured is the effect size for factorial ANOVA.
67
New cards
How many cells are there in a 2 x 3 x 3 between-subjects factorial design?
* 18
\
Correct. The way to have achieved this answer was by first multiplying 2 times 3 = 6. Then multiply 6 by 3 = 18.
\
Correct. The way to have achieved this answer was by first multiplying 2 times 3 = 6. Then multiply 6 by 3 = 18.
68
New cards
Homogenity of variance is a statistical assumption of the between groups Factorial ANOVA. true or false ?
True
Good job! This is true because we have different groups, and thus need to test for equality of variances.
Good job! This is true because we have different groups, and thus need to test for equality of variances.
69
New cards
The between groups factorial ANOVA has more statistical power than the repeated measures design. true or false
false
Great work. Correct! This is because repeated measures designs use the same participants and control for factors that cause variability between subjects
Great work. Correct! This is because repeated measures designs use the same participants and control for factors that cause variability between subjects
70
New cards
Which of the following two effect sizes can be used for the between groups factorial ANOVA?
Omega squared and eta squared
Correct. Omega and eta sqaured are both used as effect sizes for the between groups factorial ANOVA. Remember that R squared is the effect size for planned linear contrasts, not factorial ANOVAs.
Correct. Omega and eta sqaured are both used as effect sizes for the between groups factorial ANOVA. Remember that R squared is the effect size for planned linear contrasts, not factorial ANOVAs.
71
New cards
The diagram below displays the partitioning of variance for the between-subjects factorial ANOVA
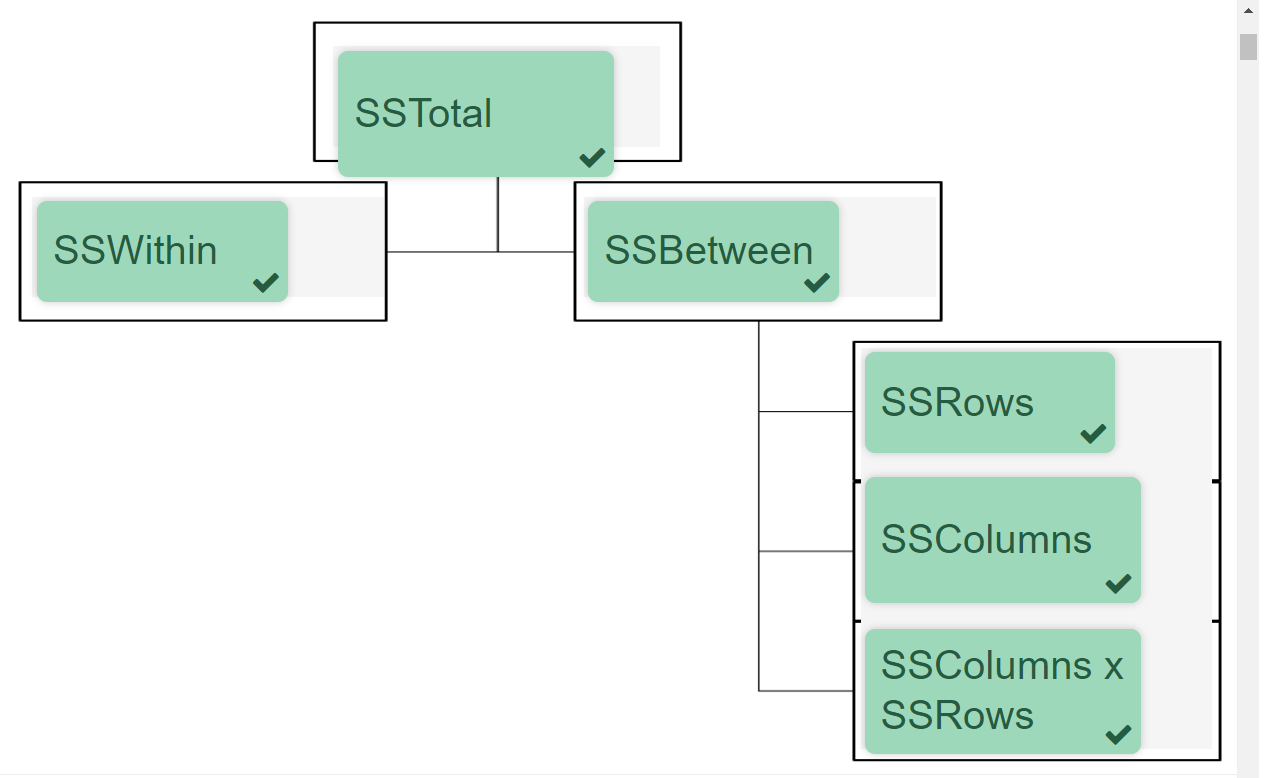
72
New cards
The F-ratio for the between-subjects factorial ANOVA uses a ratio of which two Sums of Squares for:
The main effect for columns
MS columns over MS within
\n The main effect for rows \n MS rows over MS within \n
The interaction between rows and columns \n MS columns x rows over MS within
MS columns over MS within
\n The main effect for rows \n MS rows over MS within \n
The interaction between rows and columns \n MS columns x rows over MS within
73
New cards
In a research scenario where 60 participants are equally split into 4 separate cells of data (i.e., there are 2 between-subjects IV’s, each with 2 levels), what are the values for:
a. df total
b. df column
c. df row
d. df column x row
e. df within
a. df total
b. df column
c. df row
d. df column x row
e. df within
**a. df total**
i. df total = N−1
ii. df total =60−1
iii. df total = **59**
**b. df column**
i. df column = c −1
ii. df column =2−1
iii. df column = **1**
**c. df row** \n i. df row = r −1
ii. df row =2−1
iii. df row = **1**
**d. df column x row** \n i. = df column x row (c−1)(r−1)
ii. = df column x row 1x1
iii. df column x row = **1**
**e. df within** \n i. df within =N − (c)(r)
ii. df within =60−(2x2)
iii. h = **56**
i. df total = N−1
ii. df total =60−1
iii. df total = **59**
**b. df column**
i. df column = c −1
ii. df column =2−1
iii. df column = **1**
**c. df row** \n i. df row = r −1
ii. df row =2−1
iii. df row = **1**
**d. df column x row** \n i. = df column x row (c−1)(r−1)
ii. = df column x row 1x1
iii. df column x row = **1**
**e. df within** \n i. df within =N − (c)(r)
ii. df within =60−(2x2)
iii. h = **56**
74
New cards

Using the above df calculations, when reporting the F-ratio for a between-subjects factorial ANOVA, what Degrees of Freedom values (i.e., F(?, ?) = 5.45) should be inserted inside the brackets for:
The main effect for rows
ii. *F*(, ) = 5.45
The main effect for columns
ii. *F*(, ) = 5.45
The interaction between rows and columns
ii. *F*(, ) = 5.45ii. *F*(**1**, **56**) = 5.45
\
The main effect for rows
ii. *F*(, ) = 5.45
The main effect for columns
ii. *F*(, ) = 5.45
The interaction between rows and columns
ii. *F*(, ) = 5.45ii. *F*(**1**, **56**) = 5.45
\
ii. *F*(**1**, **56**) = 5.45
The main effect for columns
ii. *F*(**1**, **56**) = 5.45
The interaction between rows and columns
ii. *F*(**1**, **56**) = 5.45
The main effect for columns
ii. *F*(**1**, **56**) = 5.45
The interaction between rows and columns
ii. *F*(**1**, **56**) = 5.45
75
New cards
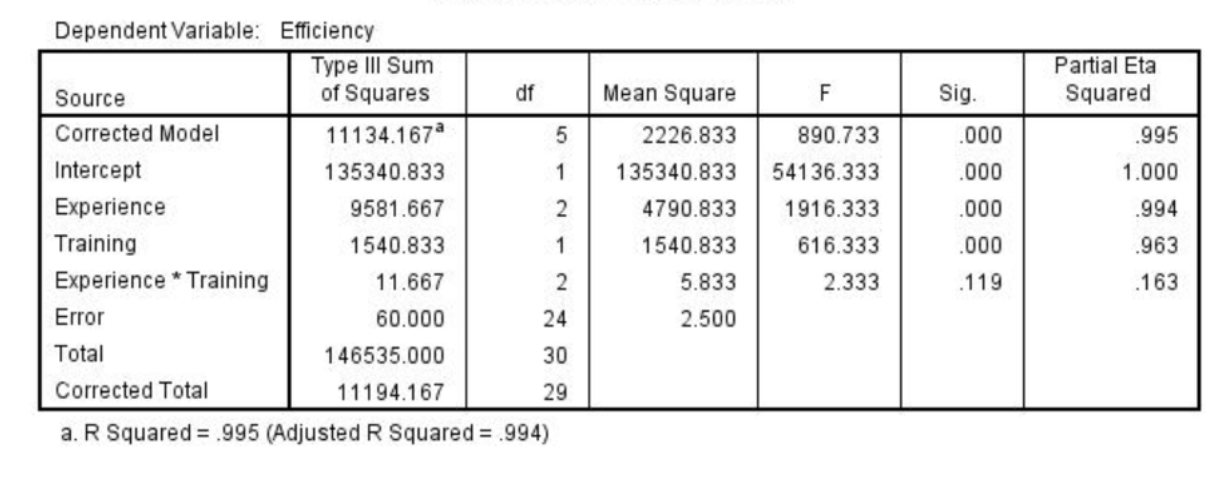
How would you write up the result for the main effect of experience?
F(, ) = , p
F(, ) = , p
F(2, 24) = 1916.33, p
76
New cards
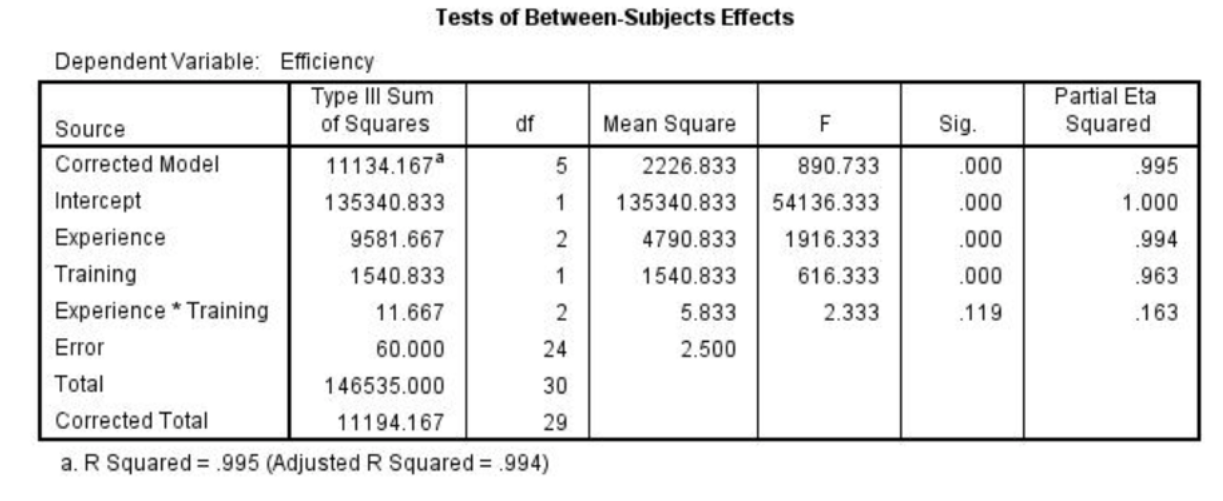
n the same ANOVA table below, there is an interaction between experience and training true or false?
False As the p value is greater than .05 (the p value is .119) the interaction is not significant.
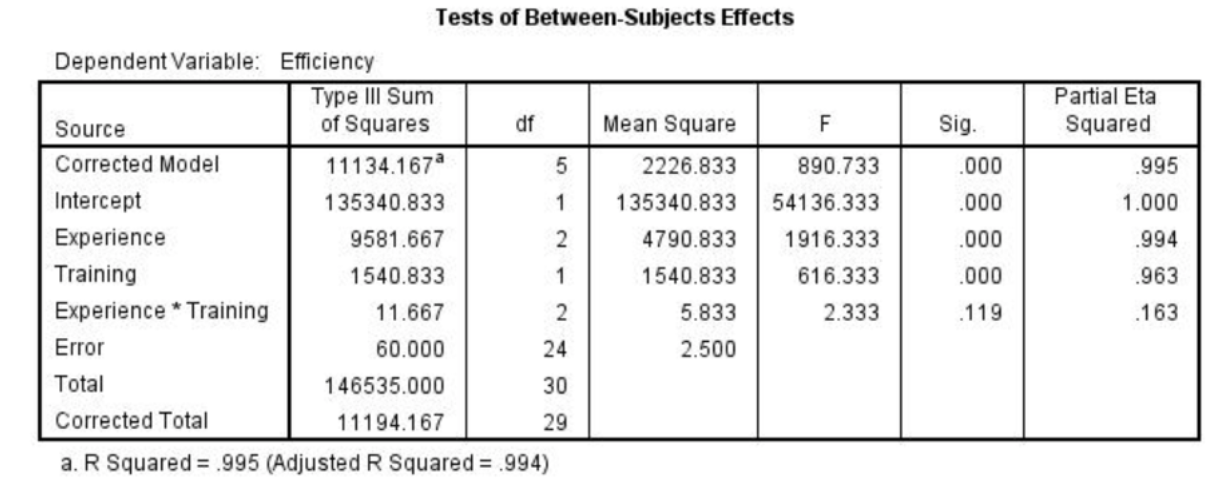
77
New cards
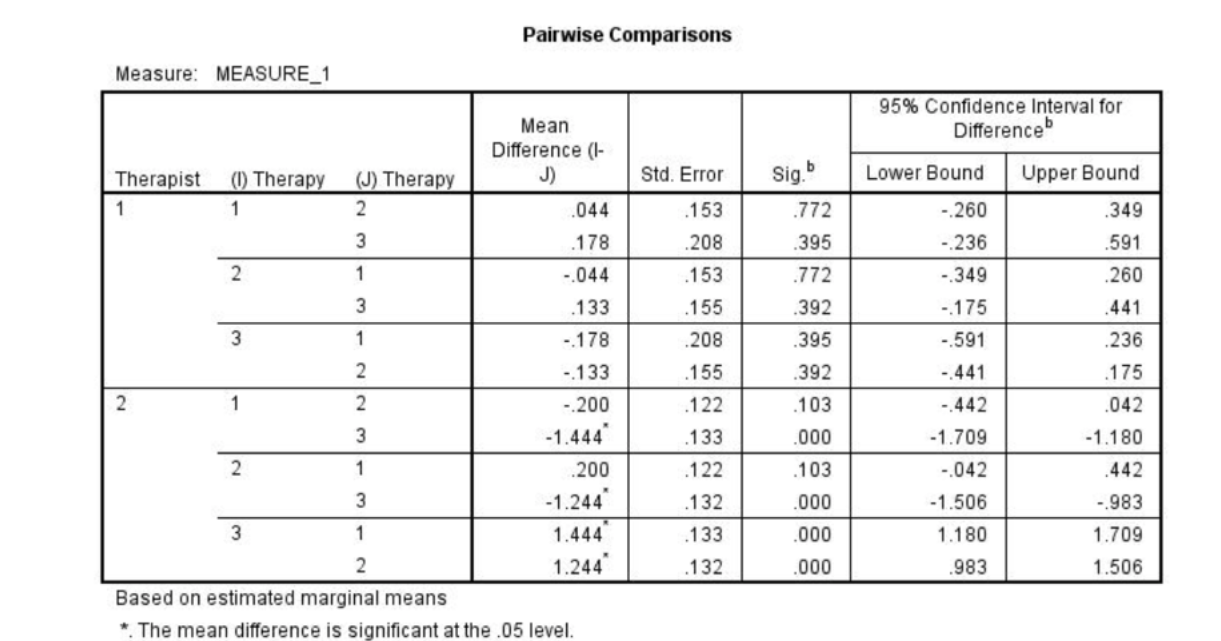
Using the output table below (and a Bonferroni adjustment of p < .016 to control for type 1 error rate), interpret, describe and report the results of the simple effects analyses for the interaction (Note: Level 1 of therapist is Therapist A and Level 2 of therapist is Therapist B; Level 1 of therapy is CBT, Level 2 of therapy is ACT, and Level 3 of therapy is ET).
For therapist A (untrained), where was no significant difference (using a Bonferroni adjusted alpha of p < .016) in likelihood of uptake across all three therapy types (all p’s > .016). For therapist B (trained), likelihood of uptake was significantly higher for ET than for both CBT (p < .001) and ACT (p < .001). Likelihood of uptake did not differ between CBT and ACT (p = .10). Overall, the results reveal that participants were more likely to pursue therapy with a trained therapist who practiced in ET rather than CBT or ACT.
78
New cards
It is possible to test for an interaction using a one-way ANOVA: true or false ?
The answer is false as there is only one IV in a one-way ANOVA, an interaction between two IVs cannot be tested.
79
New cards
If the interaction is significant in a factorial ANOVA, the main effects should be interpreted with caution: true or false ?
The answer is true because the main effects need to be investigated using simple effects.
80
New cards
If there are 2 significant main effects in a 2 x 2 factorial design, the interaction will also automatically be significant. true or false ?
false The answer is false because an interaction is not always significant when there are two main effects (as these effects could be occurring in the same direction).
81
New cards
The F-ratio for a main effect is *F* = .86. This result will be statistically significant. true or false ?
False F values generally need to approach a value of 1.00 or greater to be significant.
82
New cards
What is a simple effects analysis?
Simple effects tests are follow-up tests when the interaction is significant. They explore the nature of the interaction by examining the difference between means within one level of one of the independent variables across the levels of the other independent variable.
83
New cards
How may error terms does a Factorial Repeated-Measures ANOVA have?
One per main effect and one per interaction
84
New cards
For a fully Repeated-Measures ANOVA, we should check the assumption of:
Homogeneity of Covariance Homogeneity of covariance (or sphericity) is an assumption of a repeated measures design, whereas homogeneity of variance is a between-groups design assumption.
85
New cards
If I have a 2 x 3 x 2 factorial design, what do I know about my variables?
You have 3 IV's, each with at least 2 levels
Because there are three numbers in the design statement, this means you have three IVs. Also, because each of these numbers in the design statements are 2 or greater (the values are 2, 3, and 2) you know each of the IVs has 2 or more levels.
Because there are three numbers in the design statement, this means you have three IVs. Also, because each of these numbers in the design statements are 2 or greater (the values are 2, 3, and 2) you know each of the IVs has 2 or more levels.
86
New cards
If we find a significant main effect for BOTH IV's in a 2x2 design, we can conclude that..
There's not enough information to determine an interaction
because having significant main effects do not mean there will always be a significant interaction.
because having significant main effects do not mean there will always be a significant interaction.
87
New cards
how many levels of an IV are needed to do a repeated measures factorial ANOVA?
2 or more
For any factorial ANOVA (whether it is a between or repeated measures design), the IVs only need to have 2 or more levels.
For any factorial ANOVA (whether it is a between or repeated measures design), the IVs only need to have 2 or more levels.
88
New cards
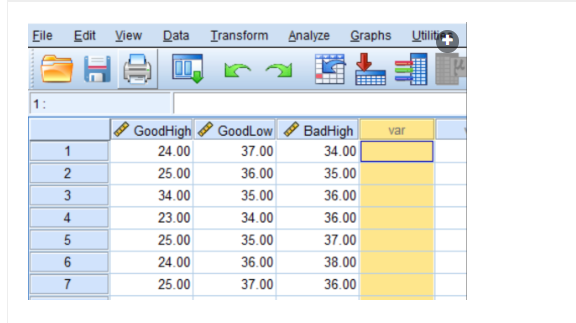
In a 2x2 Factorial Repeated-Measures ANOVA - what would be the coding for the missing column?
BadLow
89
New cards
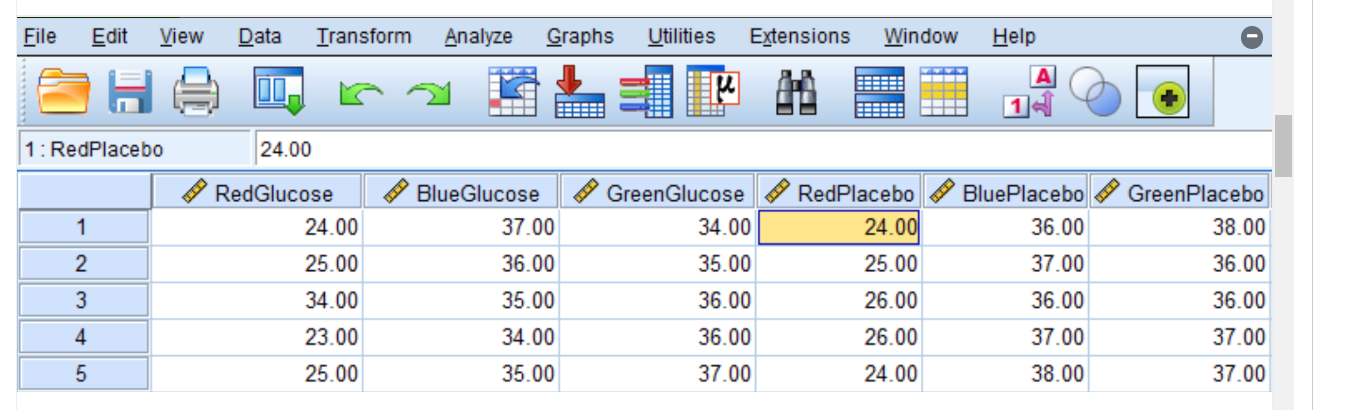
What is the design of this factorial data?
* 2 x 3 Repeated-Measures
Correct answer.
Correct. The reason being, you have one IV that would be called 'Condition' with two levels (Glucose, Placebo) and another called 'Colour' with three levels (Red, Blue, Green). The reason this data is repeated measures in nature is because the participants have a data value in every column, indicating they participated in all conditions.
Correct answer.
Correct. The reason being, you have one IV that would be called 'Condition' with two levels (Glucose, Placebo) and another called 'Colour' with three levels (Red, Blue, Green). The reason this data is repeated measures in nature is because the participants have a data value in every column, indicating they participated in all conditions.
90
New cards
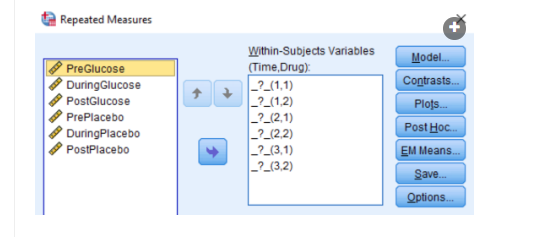
What are the first two conditions we should enter?
PreGlucose | PrePlacebo
91
New cards
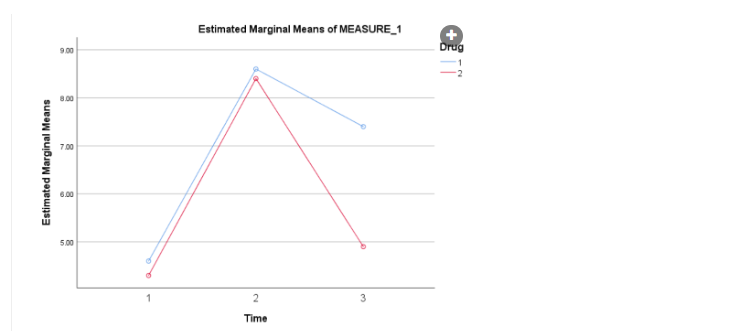
The most interesting time-point to run a simple-effects analysis on would be:
T3 Correct, because this is where the means appear to be different across the two drug conditions.
92
New cards
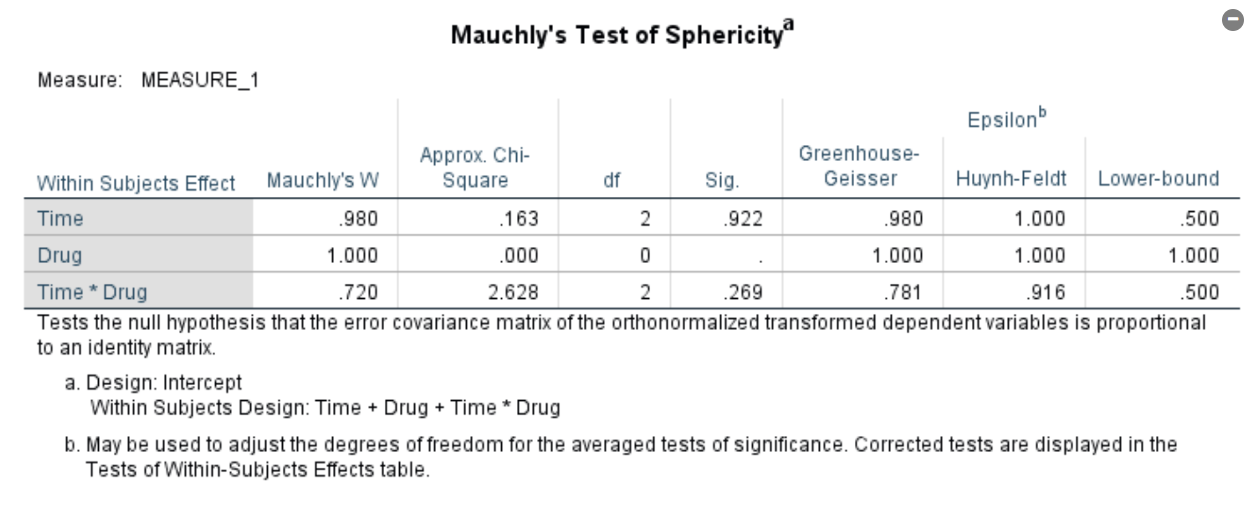
For the following output, we would say that assumption of sphericity:
Has been met for all effects Correct! Because the p values (sig column) for both the main effect of time, and the time x drug interaction were both greater than .05.
93
New cards
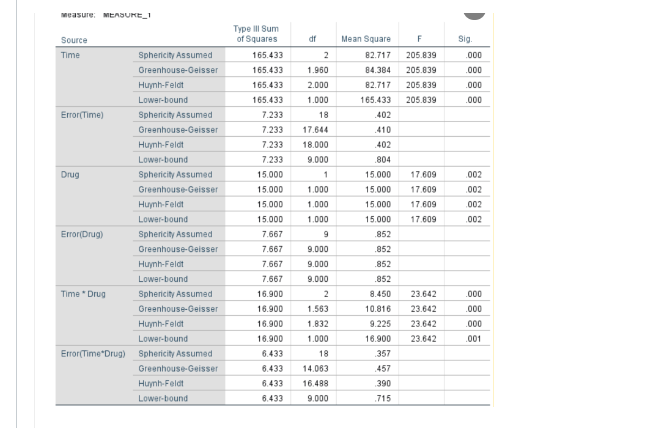
For this analysis, the interaction is:
Significant Correct, because irrelevant of whether we use Sphericity assumed or a correction, the p value (sig) for the interaction effect is less than .05. It is *p* < .001.
94
New cards
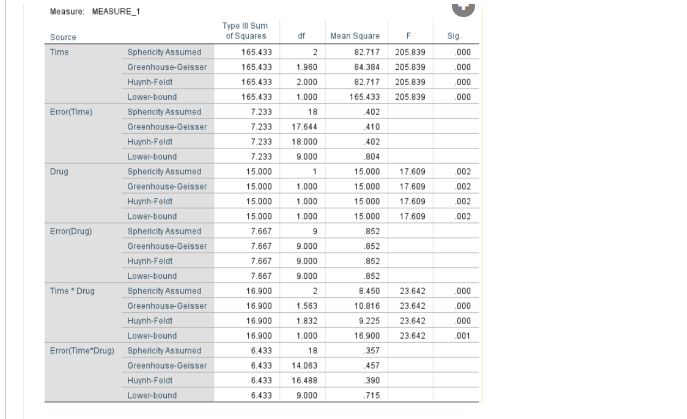
What are the degrees of freedom for the interaction effect?
(2,18)
95
New cards
What is the key feature of a mixed factorial design?
* One IV is between-groups.
* There are two or more independent variables.
* One IV is within-subjects.
* There are two or more independent variables.
* One IV is within-subjects.
96
New cards
Which Assumptions of the data need to be met for a mixed model ANOVA?
Both Homogeneity of Variance and Sphericity
both these two assumptions and nornallity are all requirements of the mixed factorial ANOVA.
both these two assumptions and nornallity are all requirements of the mixed factorial ANOVA.
97
New cards
In a mixed-factorial design, the interaction term between two between-groups factors would be:
* In the between-groups effects table
\
Correct, between-groups interactions would be in the between-group effects table.
\
Correct, between-groups interactions would be in the between-group effects table.
98
New cards
In a mixed-factorial design, the interaction between two repeated-measures factors would be:
In the within-subjects effects table
Correct, within-subjects effects and interactions are only displayed in the within subjects table.
Correct, within-subjects effects and interactions are only displayed in the within subjects table.
99
New cards
The interaction term between a repeated-measures and between-group factor would be:
* In the within-subjects effects table
\
Correct, for interactions that have a within-subjects AND a between-subjects factor, these will be in the within-subjects effects table.
\
Correct, for interactions that have a within-subjects AND a between-subjects factor, these will be in the within-subjects effects table.
100
New cards
In a 2x3 Mixed Factorial design - which factor is within, and which factor is between:
No way to tell