Math V - w3, w4

First Order Differential Equations

First Order Differential Equations

Some important concepts:

For 4 types of first order ODEs, general method can be used to find solutions:

For 4 types of first order ODEs, general method can be used to find solutions

Type 1

For 4 types of first order ODEs, general method can be used to find solutions

Type 2

For 4 types of first order ODEs, general method can be used to find solutions

Type 3

For 4 types of first order ODEs, general method can be used to find solutions

Type 4

First Order ODE

Alternative method

Sometimes the effort of finding an analytical solution is not justified by the costs.

In such cases we often resort to numerical methods:

In this course, we consider Picard’s method to numerically approximate the solution of an initial value problem.

Before we can formally derive why this method works, we need to introduce some concepts

Picard’s method

Introducing some concepts first 1

Picard’s method

Introducing some concepts first 2

Picard’s method

Stability of Differential Equations

Neutrally stable

Stability of Differential Equations

Asymptotically stable / unstable

Autonomous first order ODE

Autonomous first order ODE

If F is C¹

Second Order Differential Equations

Second Order Differential Equations

Solution

Systems of Differential Equations

First order

Systems of Differential Equations

Example

Systems of Differential Equations

The scalar ODE

Linear Vectorial ODEs

Solution to a system of homogeneous ODEs

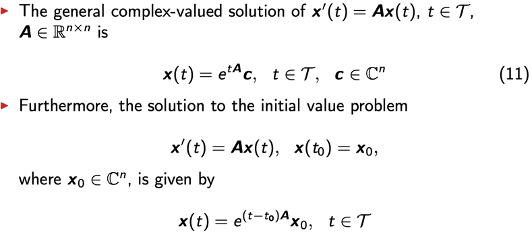
The sum of elements of a linear space are an element of the linear space.

Example

Fundamental Matrix of a linear differential equation

Once you have found a complex-valued basis of the solution space, you can construct a real-valued basis:

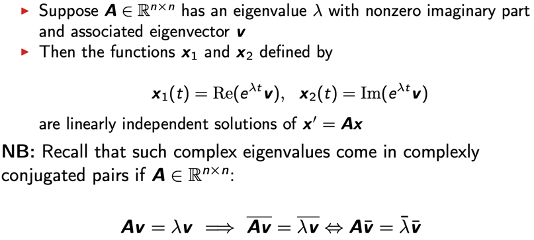
General Solutions of Linear Higher Order ODEs

1

General Solutions of Linear Higher Order ODEs

2

Stability of Solutions of Higher Order ODEs

Neutrally stable

Stability of Solutions of Higher Order ODEs

Asymptotically stable / unstable

Null solution of homogeneous equation

The stability properties of solutions of inhomogeneous ODEs coincide with

The stability properties of solutions of inhomogeneous ODEs coincide with those of the null solution of the associated homogeneous ODE:

Stability of nonlinear autonomous system of ODEs

Determining stability properties of solutions of scalar ODE trick

Phase portrait

Graphic illustrations are helpful when studying stability of systems of differential equations

Suppose you have constructed a phase portrait of a given planar ODE with equilibrium point a, then: