AP BC Formulas to know

sin2x =

2sinxcosx

Pythagorean Identities

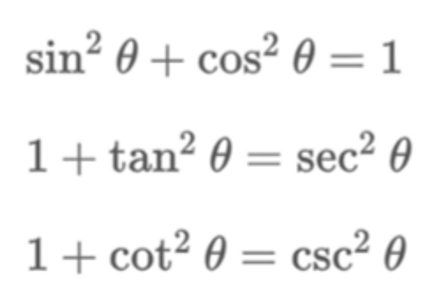
sin(-x) =

-sinx

sin (A ± B)

• sin (A + B) = sinAcosB + cosAsinB

• sin (A - B) = sinAcosB - cosAsinB

Law of Cosines

a^² = b² + c² - 2bc⋅cosA

Distance Between 2 Points

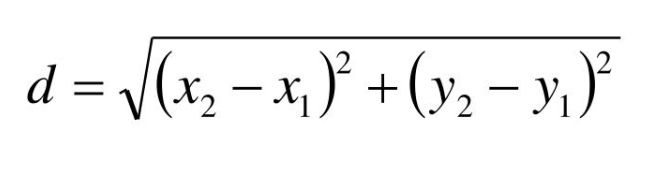
Midpoint Formula

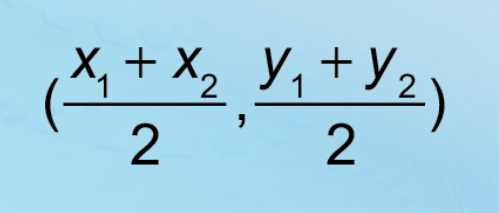
Laws of Logarithms — ln(ab) =

ln(a) + ln(b)

Laws of Logarithms — ln(0) =

undefined

Laws of Logarithms — ln(a/b) =

ln(a) - ln(b)

Laws of Logarithms — ln(1) =

0

Laws of Logarithms — ln(aⁿ) =

(n)ln(a)

Laws of Logarithms — ln(e) =

1

Laws of Logarithms — ln(1/a) =

-ln(a)

Definition of a Limit

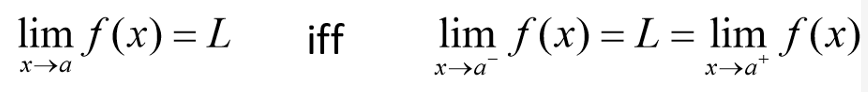
Limit Laws—lim_x→a(f ± g) =

lim_x→a (f) ± lim_x→a (g)

Definition of Continuity at a Point

Intermediate Value Theorem Conditions

If:

• f is continuous on a closed interval [a,b]

• f(a) does NOT equal f(b) —→ start point doesn’t equal end point

• k is between f(a) and f(b)

Then there exists a number c between a and b for which f(c) = k

Definition of |x|

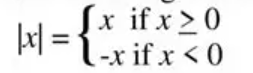
Squeeze Theorem

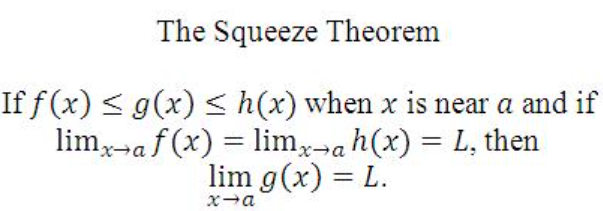
cos²x = 

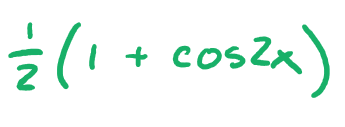
sinAcosB =

Definition of VA

Definition of HA

Average Rate of Change (AROC)

the slope of the secant line between 2 points

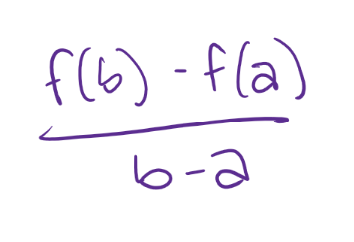
Common limits—lim_x→-∞ e^x =

0

Common limits—lim_x→∞ e^x →

∞

Common Limits—lim_x→0+ ln(x) →

-∞

Common limits—lim_x→∞ ln(x) →

∞

Common limits—lim_x→0 (e^x - 1) / x =

1

Common limits—lim_x→0 sin(x)/x =

1

Common limits—lim_x→0 1-cos(x)/x =

0

Common limits—lim_x→a x =

a

Common limits—lim_x→+-∞ (1 + (c/x))^x =

e^c

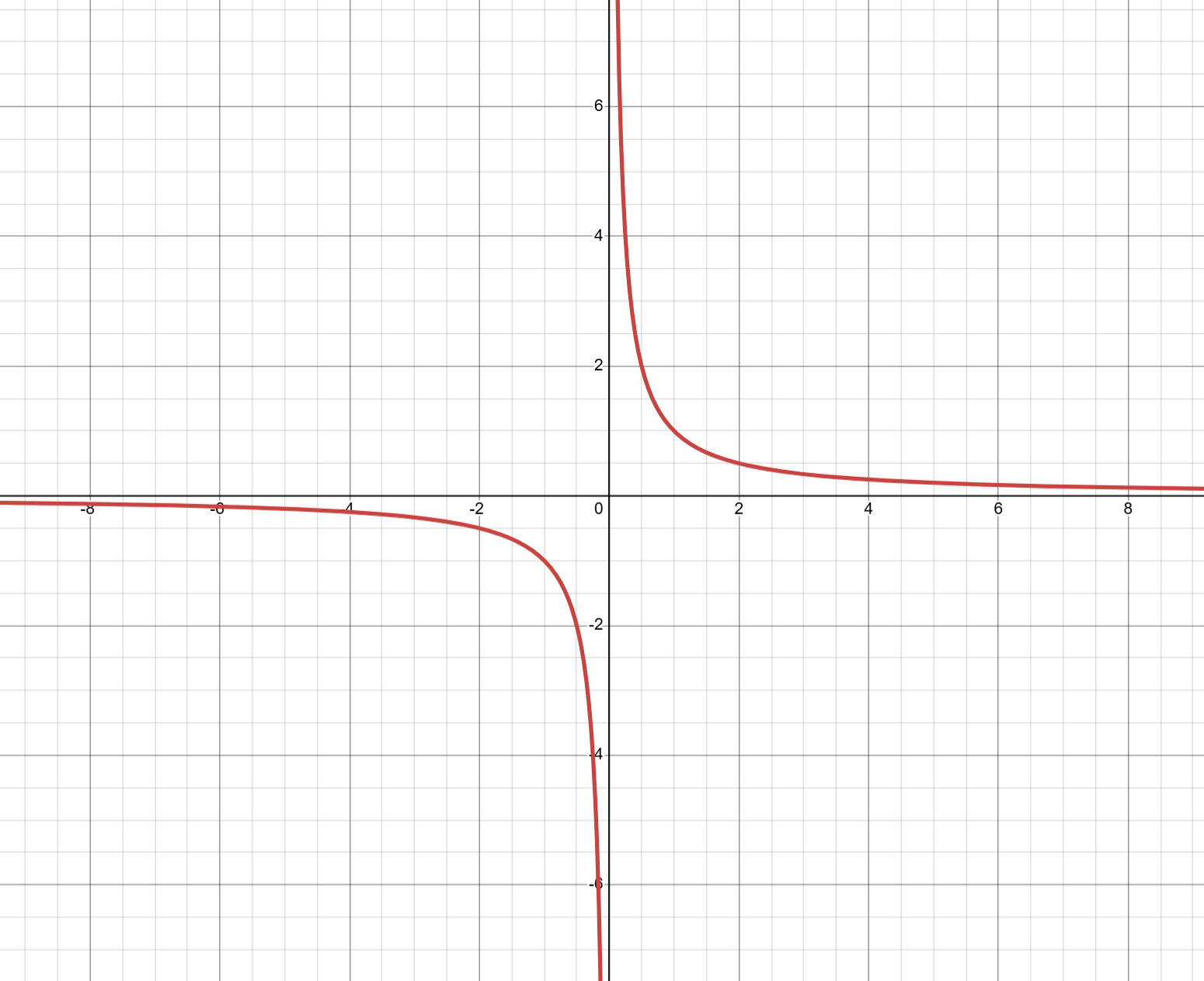
graph of 1/x

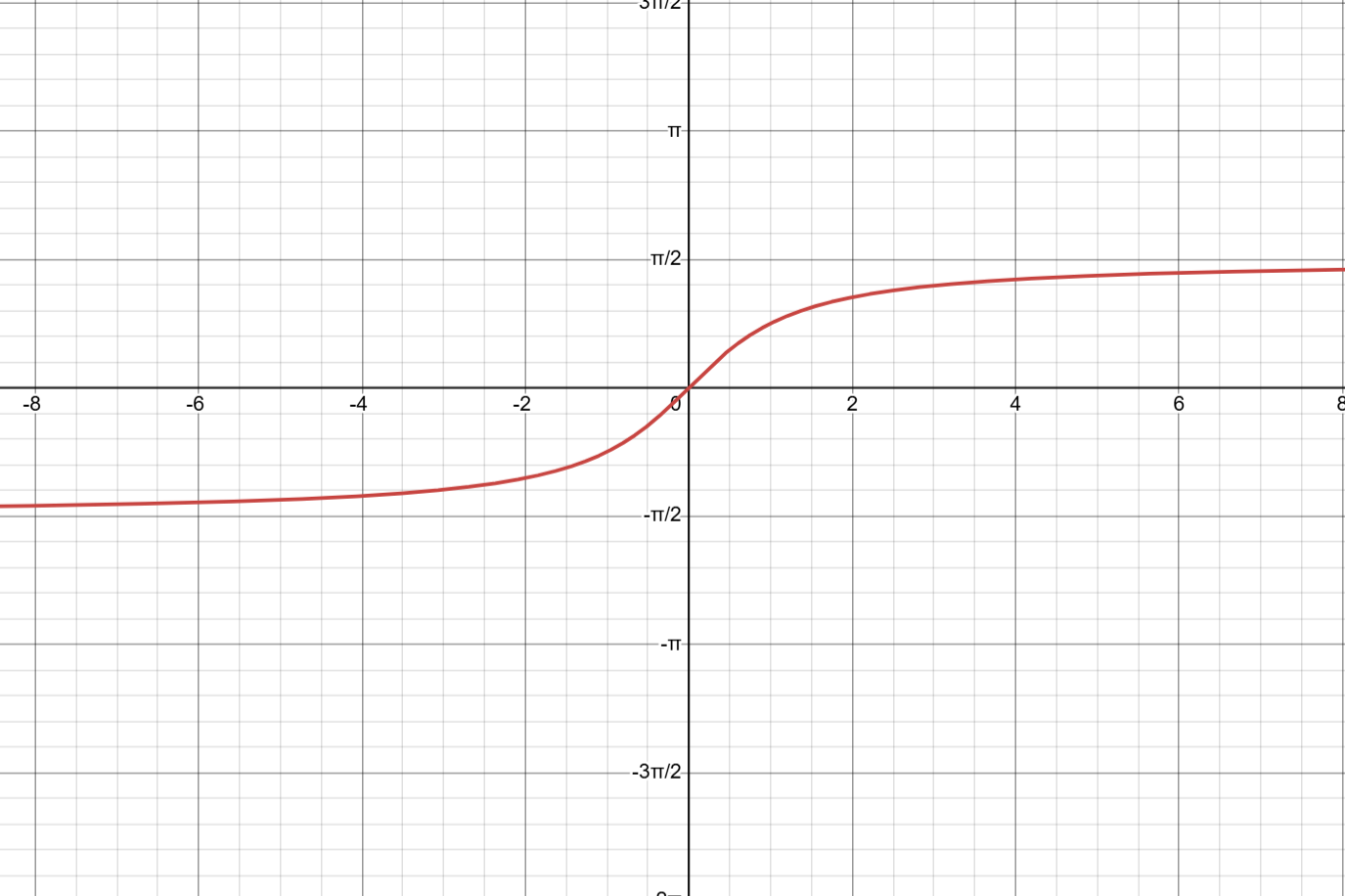
graph of arctan(x)

Definition of the derivative

will give an equation

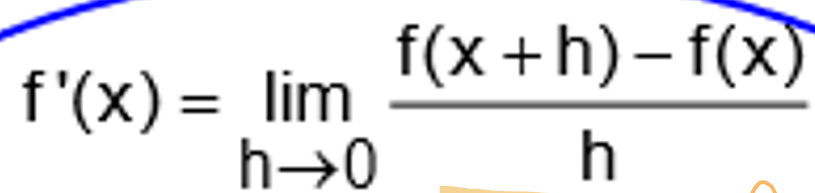
Alternate form of definition of the derivative

will give a number

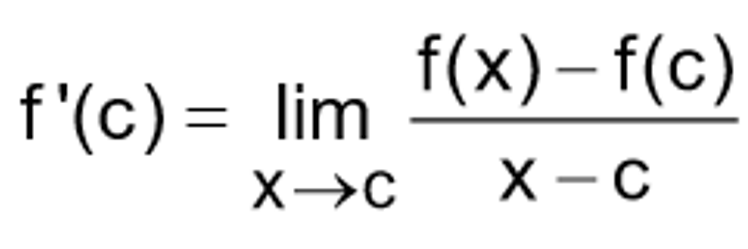
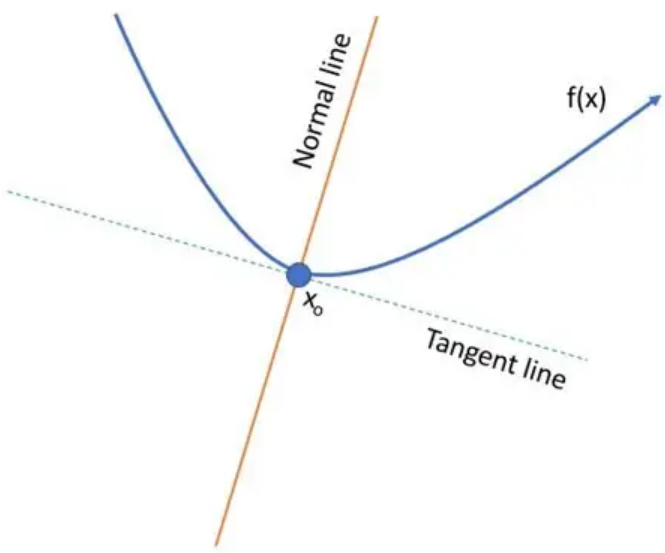
Normal Line

the line perpendicular to the tangent line at the point of tangency

3 reasons a function (f) won’t be differentiable at a point x = a

1. f is not continuous at x = a

2. the graph of f has a “corner” or a “cusp” at x = a

3. the graph of f has a vertical tangent at x = a

d/dx (e^x) =

e^x

d/dx (lnx) =

1/x

d/dx (log_ax) =

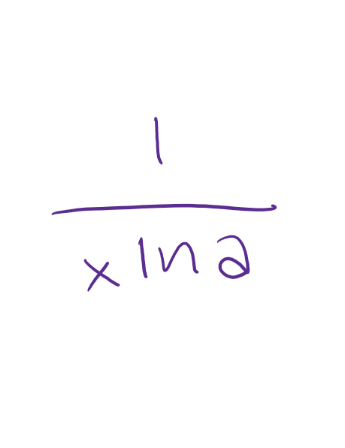
d/dx (a^x) =

a^xln(a)

d/dx (constant) =

0

d/dx ( constant ⋅ f) =

constant ⋅ f’

d/dx (f±g) =

f’ ± g’

What does the maximum or minimum values refer to?

Refer to the y-value

s(t) =

position

v(t) =

instantaneous velocity — can be found by finding the derivative of the position function s’(t)

abs(v(t)) =

Speed — simply the absolute value of velocity

a(t) =

Acceleration — find 2nd derivative of position function s’’(t)

d/dx [f(x)g(x)]

f’g + fg’

Quotient Rule—d/dx [f(x)/g(x)]

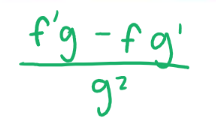
d/dx (sinx) =

cosx

d/dx (cosx) =

-sinx

d/dx (tanx) =

sec² x

d/dx (cotx) =

-csc² x

cos2x =

• cos²x - sin²x

• 2cos²x -1

• 1 - 2sin²x

d/dx (cscx) =

-cscx ⋅ cotx

d/dx (secx) =

secx ⋅ tanx

cos (A ± B)

• cos (A + B) = cosAcosB - sinAsinB

• cos (A - B) = cosAcosB + sinAsinB

Limit Laws—lim_x→a (c ⋅ f) =

c ⋅ lim_x→a (f)

Limit Laws—lim_x→a (f/g) =

lim_x→a (f)/lim_x→a (g)

Limit Laws—lim_x→a (fg) =

lim_x→a (f) ⋅ lim_x→a (g)

Limit Laws—lim_x→a (ⁿ√f(x) )=

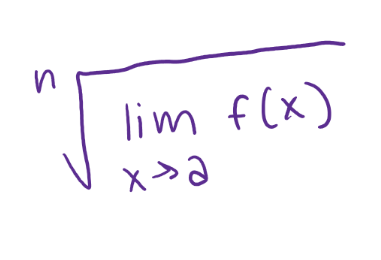
Limit Laws—lim_x→a (f(g(x)) =

f(lim_x→a (g(x)))

Limit Laws—lim_x→a (k) =

k

Limit Laws—lim_x→a (x) =

a

cosAsinB =

sinAsinB =

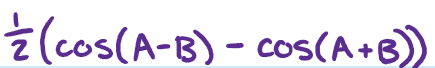
cosAcosB = 

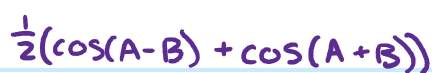
cos(-x) =

cosx

tan(-x) =

-tanx

sin²x =

Particle is at rest when . . .

v(t) = 0

speed is increasing if:

v and a have the same sign

speed is decreasing if:

v and a have opposite signs

Linear approximation

y - y₁ = m (x - x₁)

d/dx [f^-1(x)] =

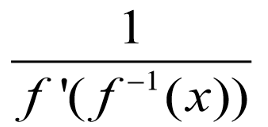
d/dx (sin^-1x) =

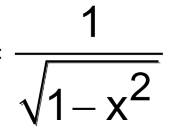
d/dx (cos^-1x) =

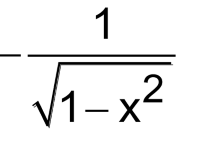
d/dx (tan^-1x) =

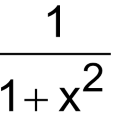
d/dx (csc^-1x) =

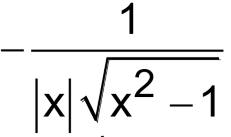
d/dx (sec^-1x) =

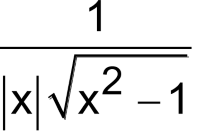
d/dx (cot^-1x) =

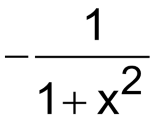
L’Hopitals Rule

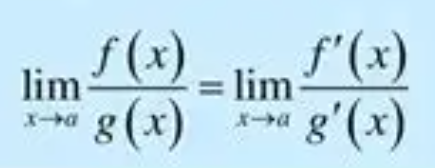
Extreme Value Theorem

1. If cont. [a,b]

2. Then f has an absolute max or min on [a,b]

Stationary point

f(c) = 0

Singular point

f’(c) is undefined

Rolle’s Theorem 

If:
   1. f is cont. on []

2. Differentiable on ()

3. f(a) = f(b)

Then:
   - there is at least one number c on () such that f’(c) = 0

Mean Value Theorem

If:
1. f is cont. []

2. Differentiable on ()

Then:
- there exists a number c between a and b such that f’(c) = (f(b) - f(a)) / b - a