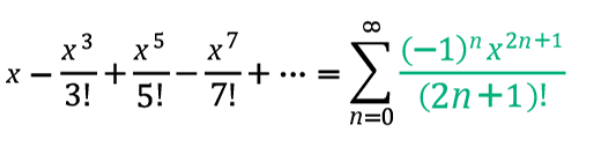Calculus 2

d/dx cosx

-sinx

d/dx sinx

cosx

d/dx cotx

-csc^2(x)

d/dx tanx

sec^2(x)

d/dx secx

secxtanx

d/dx cscx

-cscxcotx

int cosx

sinx

int sinx

-cosx

int tanx

-ln|cosx| or ln|secx|

int secx

ln|secx+tanx|

int cscx

ln|cscx-cotx|

int sec^2(x)

tanx

int cscxcotx

-cscx

int secxtanx

secx

int csc^2(x)

-cotx

int cotx

ln|sinx|

Definition of e

lim k->infinity of

(1 + (1/k))^k

Which diverges by ration Test because e>1

(a^k)/(b^k)

(a/b)^k factoring out the power.

(k + 1)!

(k + 1)k!

2^(k + 1)

2 • 2^k

1 + cot^2(x)

csc^2(x)

tan^2(x) + 1

sec^2(x)

d/dx e^(u(x))

e^(u(x)) • u'(x)

d/dx e^x

e^x

int e^x dx

e^x + c

e

e^x will always be positive

d/dx ln(u)

1/u • du/dx

int (1/u) du

ln |u| + c

A of circle

pi • r^2

b^x

e^(x(lnb))

d/dx [arcsin(x)]

1/(sqrt: 1 - x^2)

d/dx [arctan(x)]

1/(x^2 + 1)

d/dx [arccos(x)]

-1/(sqrt: 1 - x^2)

d/dx [arccot(x)]

-1/(x^2 + 1)

d/dx [arcsec(x)]

1/ (|x|(sqrt: x^2 - 1))

d/dx [arccsc(x)]

-1/ (|x|(sqrt: x^2 - 1)

Integration by parts

uv - int: vdu

General Slicing Method

V= int: A(x)dx

Disk Method

V= int: pi[f(x)]^2 dx

Washer Method

V= int: piRouter^2 - piRinner^2 dx

Arc Length

L= int: sqrt ( (dy/dt)^2 + (dx/dt)^2) dy

tan^2(x)+1

sec^2(x)

Adjusting the starting index

from 1 to 0

Replace all the instances of n in the series with n+1

Geometric Series

S(n)=

Geometric Series

|r| < 1 converges

sum = a/(1-r)

Ratio Test

r<1 converges

r> diverges

r=1 inconclusive

Comparison Test

Find Bn>An if it converges then An converges.

Find Bn

P Test

P 1 series converges

Converges to 1/(p-1)

LCT

Take lim An/Bn. Choose Bn which you know if it converges/diverges.

Lim L, An and Bn converge or diverge together

Integral Test

Positive & decreasing. If integral converges --> series diverges; if ingtegral diverges --> series diverges

Series

Summation of sequence

Sequence

Set of numbers

LHopital

When lim fx and lim gx equals zero or pos/neg infinity. Lim of fx/gx equals lim f'x/g'x.

sin^2(x)

(1-cox2x)/2

Integral Remainder Theorem

int from n+1 to infinity of (f(x)dx <= R <= int fron n to infinity f(x)dx in

Alternating Series Test

if series is alternating

if Bn is positive

bn's are decreasing; Bn+1 <= Bn

limBn --> 0

series converges

Alternating Series Remainder theorem

|R| <= Bn+1 / R

Power series

Cn(x-a)^n

a = center

cn = coefficients

x = variable

Radius of Convergence

how far x can get from the center and the series can still converge; 1/2 of interval of convergence

Approximating Fn's w Power Series

put in form 1/1-(..)

Taylor Series

method for representing functions as a power series

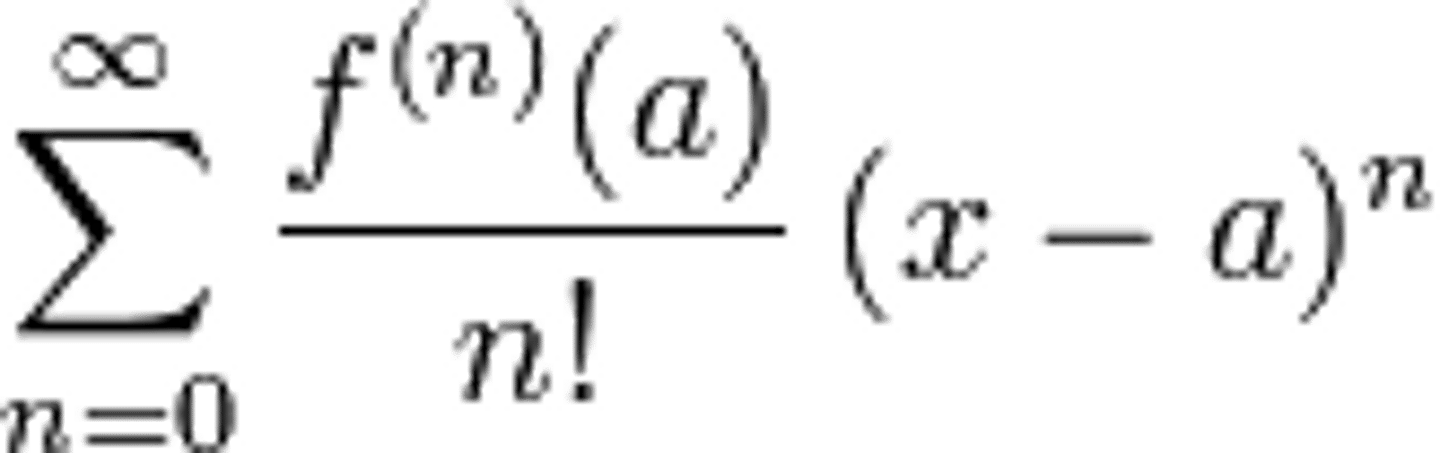
Maclaurin Series

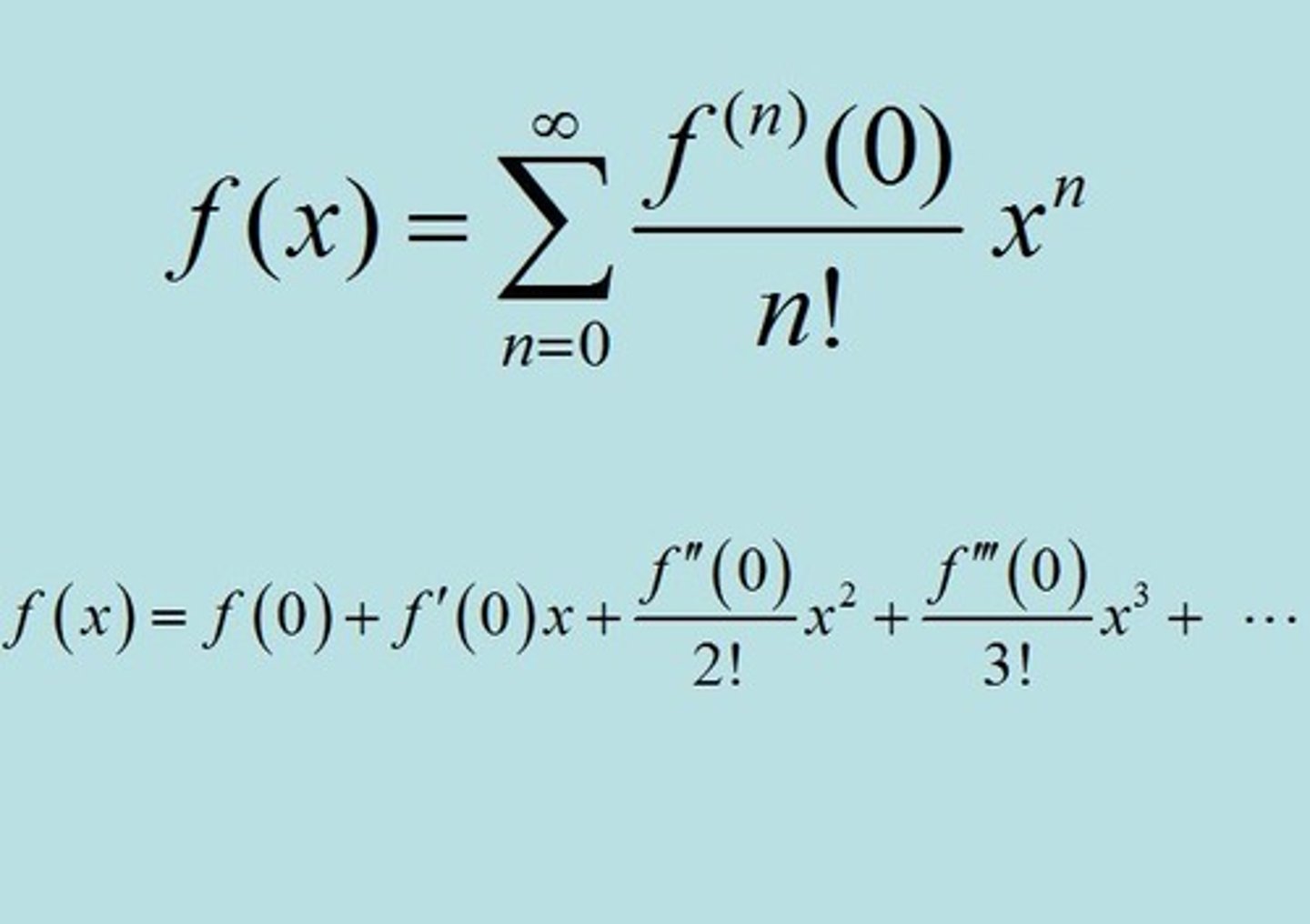
Taylor Series Remainder

Taylor's Inequality:

|Rn(x)| <= M/n+1! |x-a|^n+1

Average Value of a Fn

int a to b ( f(x)dx) / b -a

on a continuous fn will always go through its average value

cos^2(x)

1/2 + 1/2cos2x

sin^2(x)

1/2 - 1/2cos2x

cos(2x)

cos^2(x) - sin^2(x)

Integrating Trig Powers

if sin is odd and cos even --> set aside a sin and u sub w cos

if sin is even and cos is odd --> set aside a cos and u sub w sin

if both odd --> choose either sin or cos to set aside and u sub w the other

if both even --> use different identities to reduce the exponents or number of sin and cos factors

work

force * distance

w varying force or distance

w = int a to b ( Force(x) dx )

Area between curves

int a to b ( large - small) or (top - bottom) or (right - left)

Trig Sub: sqrt(a^2 - x^2)

x = asin(x) and 1 - sin^2 = cos^2

Trig Sub: sqrt( a^2+x^2)

x = atan(x) and 1 + tan^2(x) = sec^2

Trig Sub: sqrt(x^2 - a^2)

x = asec(x) and sec^2 - 1 = tan^2

integrals of partial fractions will always work when

denominator factors into linear functions

and degree of numerator is lower than degree of denominator --> if not do long division and test the Remainder

series converges if

limit exists as a finite number

if lim of an doesn't go to zero

series cannot converge

if a sereis is bounded and monotonic

it will always converge

sin(2x)

2sin(x)cos(x)

int 1/(X^2 + a^2)

(1/a)arctan(x/a)

int lnx

xlnx - x

Ranking Growth Rate

ln^a(x) << x^a << a^x << x^x

inf + inf

determinate = inf

inf * inf

determinate

0/infinity

determinate = 0 * (1/inf) = 0

inf/0

determinate = inf * 1/0 = inf

inf / inf

indeterminate

0 / 0

indeterminate

inf * 0

indeterminate

inf - inf

indeterminate

0^0

Indeterminate

1^inf

Indeterminate

inf^inf

indeterminate

0^inf

determinate = 0

lim

x -> inf f(x)/g(x) = inf

f grows faster than g

lim

x -> inf g(x)/f(x) = 0

f grows faster than g

d/dx f(g(x))

f'(g(x)) + g'(x)

d/dx f(x)g(x)

f'(x)g(x) + g'(x)f(x)

1/(1-x)

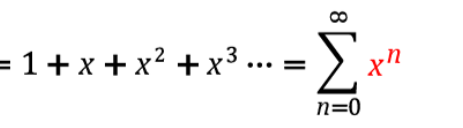
e^x

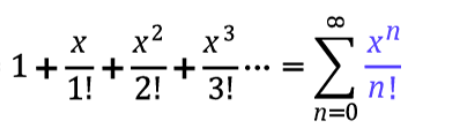
sin (x)