Comprehensive Trigonometry Review: Unit Circle, Identities, Graphs, and Formulas

Angle Measure

Angles can be measured in 2 ways, in degrees or in radians.

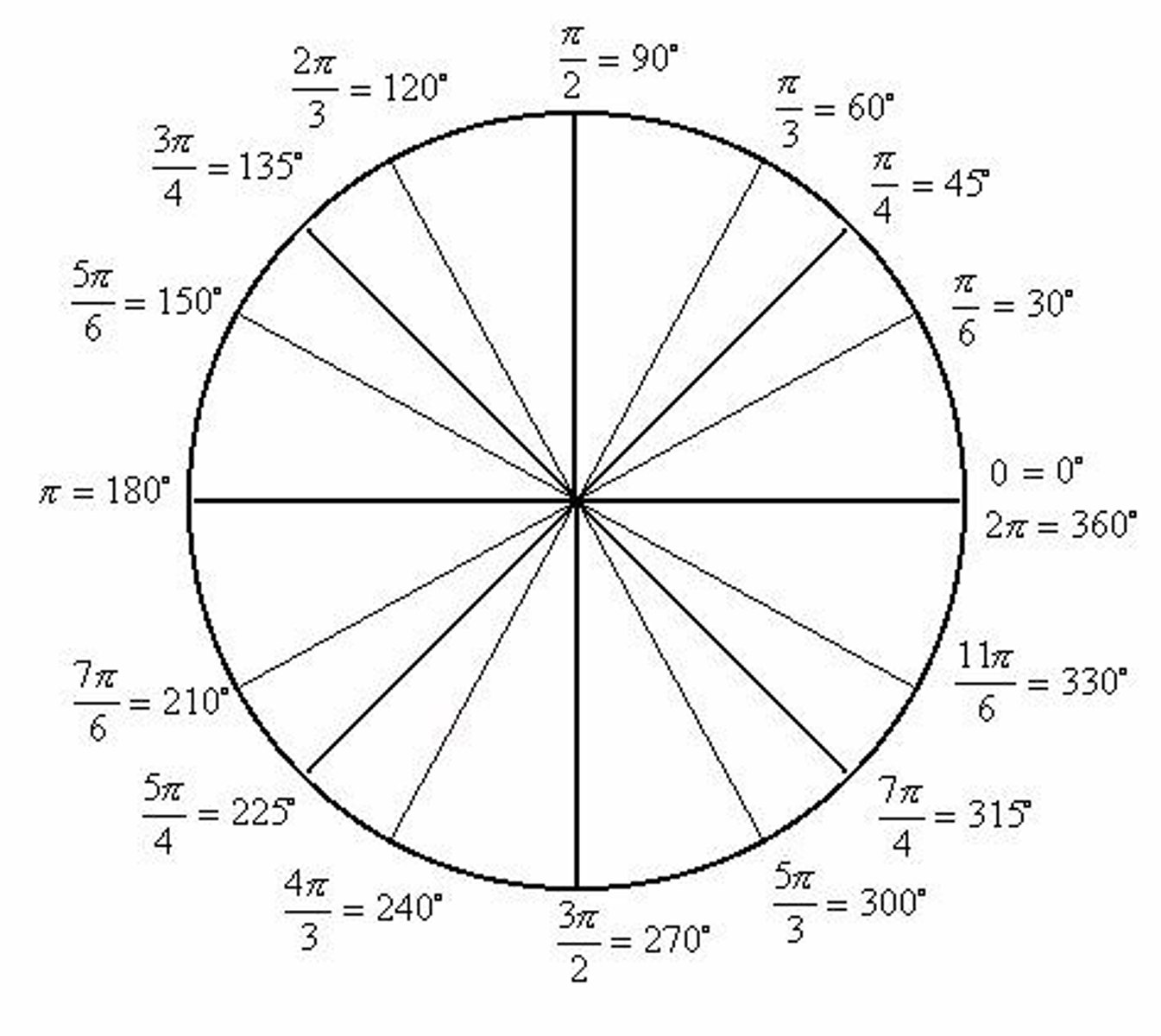
Degrees

Degrees will always have the degree symbol above their measure, as in '45°'.

Radians

Radians are real numbers without any dimensions, so the number '5' without any symbol represents an angle of 5 radians.

Positive Angles

Positive angles start on the positive x-axis and rotate counterclockwise.

Negative Angles

Negative angles start on the positive x-axis and rotate clockwise.

Conversion from Radians to Degrees

The official formula is θ = radians × (180/π).

Conversion from Degrees to Radians

The conversion formula is radians = θ × (π/180).

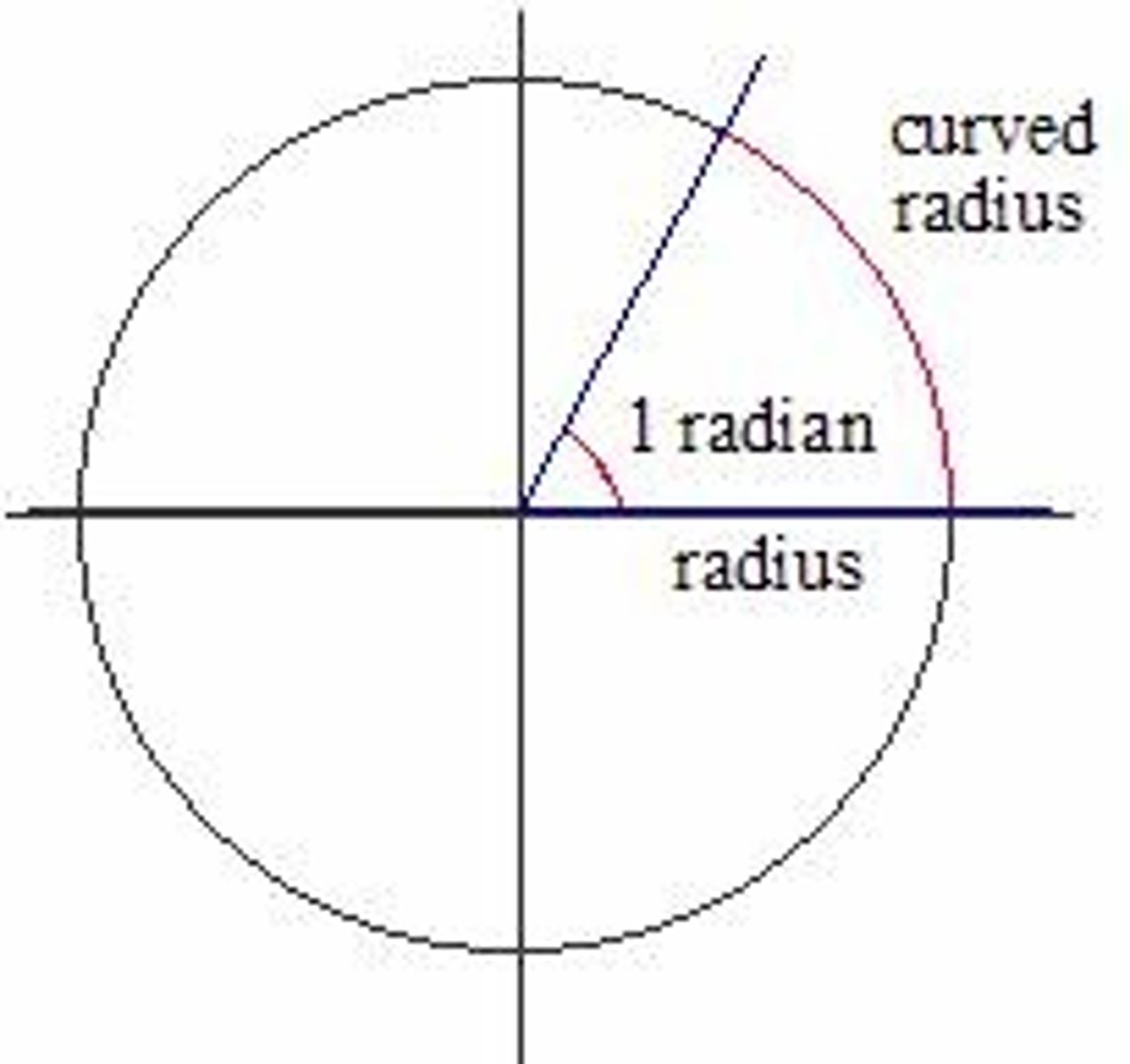
1 Radian

1 radian is approximately 57.30 degrees.

Arc Length Formula

Arc length = (radius) × (degree measure in radians).

Arc Length Variation

s = rθ, where s is arc length, r is radius, and θ is in radians.

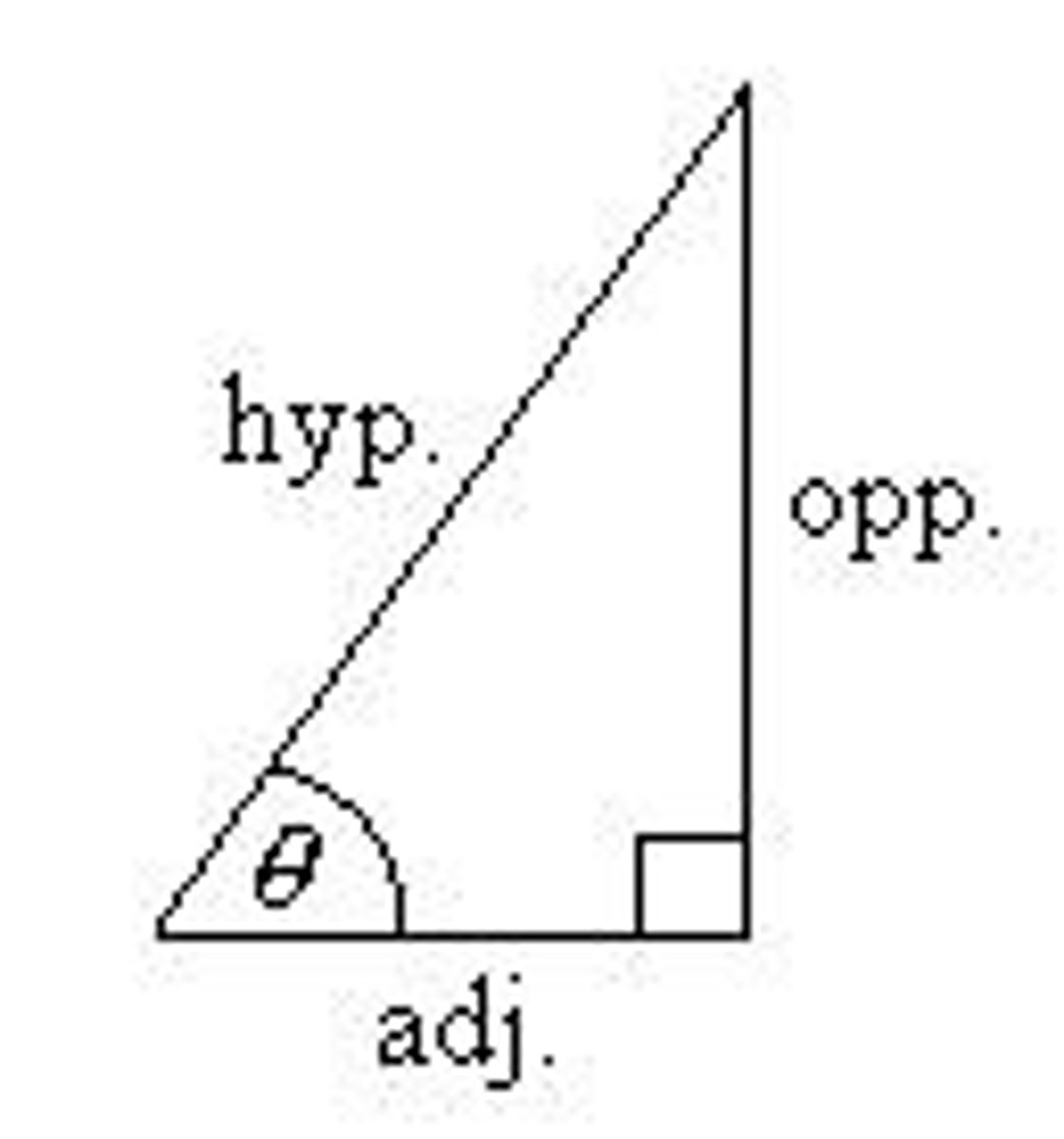
Trigonometric Ratios

The six trigonometric ratios are defined based on a right triangle and the angle θ.

SOH CAH TOA

sinθ = opp/hyp, cosθ = adj/hyp, tanθ = opp/adj.

Reciprocal Functions

cscθ = hyp/opp, secθ = hyp/adj, cotθ = adj/opp.

Finding Trigonometric Functions

To find the exact values of all 6 trigonometric functions, determine the sides of the triangle.

Adjacent Side

The side adjacent to angle θ in a right triangle.

Opposite Side

The side opposite to angle θ in a right triangle.

Hypotenuse

The hypotenuse is the longest side of a right triangle.

Special Angles

The special angles include 30° (π/6), 45° (π/4), and 60° (π/3).

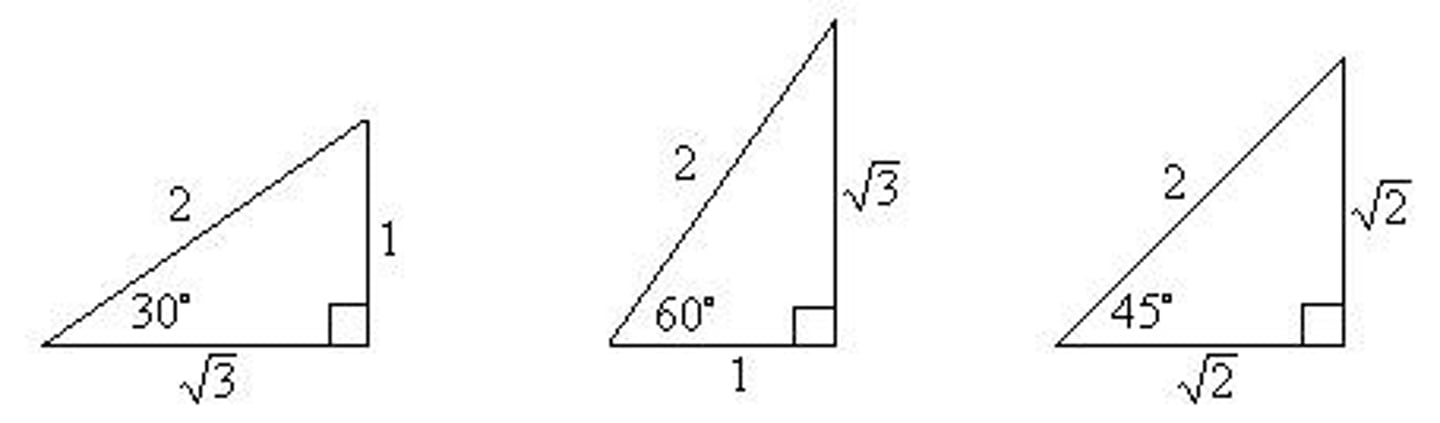
Triangle for 30°

For 30°, the triangle is defined by D = π/6.

Triangle for 45°

For 45°, the triangle is defined by D = π/4.

Triangle for 60°

For 60°, the triangle is defined by D = π/3.

Sine

sin(θ) = opp/hyp

Cosine

cos(θ) = adj/hyp

Tangent

tan(θ) = opp/adj

Cosecant

csc(θ) = hyp/opp

Secant

sec(θ) = hyp/adj

Cotangent

cot(θ) = adj/opp

Domain of Sine and Cosine

All real numbers

Range of Sine and Cosine

[-1, 1]

Periodicity of Sine and Cosine

sin(t + 2πn) = sin(t) and cos(t + 2πn) = cos(t) for any integer n

Special Angle 30°

D = π/6

Special Angle 45°

D = π/4

Special Angle 60°

D = π/3

Value of sin(0)

0

Value of cos(0)

1

Value of tan(0)

0

Value of sin(π/2)

1

Value of cos(π/2)

0

Value of tan(π/2)

undefined

Value of sin(π)

0

Value of cos(π)

-1

Value of tan(π)

0

Value of sin(3π/2)

-1

Value of cos(3π/2)

0

Domain of sine and cosine functions

All real numbers; graphs continue to the left and right in the same sinusoidal pattern.

Range of sine and cosine functions

[−1, 1]

Amplitude

The coefficient in front of the sine or cosine function that stretches or shrinks its y-values.

Example of amplitude

For y = cos(x), amplitude = 1; for y = 2cos(x), amplitude = 2; for y = 1/2 cos(x), amplitude = ½; for y = -2cos(x), amplitude = 2 with reflection in x-axis.

Period

The length of the function's cycle, which can change with a coefficient in front of x.

Standard period for sine and cosine

The usual cycle is on the interval [0, 2π].

Period formula with coefficient b

The period of y = a sin(bx) and y = a cos(bx) is found by dividing 2π by b.

Effect of b > 1 on period

Causes the graph to shrink horizontally because the period will be less than 2π.

Effect of 0 < b < 1 on period

Causes the graph to stretch horizontally making the period greater than 2π.

Key points of the graph

Found by dividing the period length into 4 increments.

Example of graphing sine function

Sketch a graph of y = (1/4)sin(2x) by hand; amplitude is 2.

Example of graphing cosine function

Sketch the graph of y = -8cos(10x); amplitude is 8, reflected in x-axis.

Period for y = -8cos(10x)

The period is found by solving the inequality 0 ≤ 10x ≤ 2π, resulting in 0 ≤ x ≤ π/5.

Translations or Phase Shift

Determined by setting up an inequality for the function and solving for x.

Example of phase shift

For y = 0.25cos(4x + 2), amplitude = 0.25, period = 2π, determine the phase shift interval.

Phase Shift

The horizontal shift left or right for periodic functions, determined by the value of c in the function f(x) = a sin(b(x - c)) + d.

Vertical Shift

The upward or downward displacement of a graph, determined by the value of d in the function f(x) = a sin(b(x - c)) + d.

Reciprocal Identities

Identities that express trigonometric functions in terms of their reciprocals, such as sin(u) = 1/csc(u).

Quotient Identities

Identities that express tangent and cotangent in terms of sine and cosine, such as tan(u) = sin(u)/cos(u).

Even Identities

Identities that show that certain functions are even, such as cos(-u) = cos(u).

Odd Identities

Identities that show that certain functions are odd, such as sin(-u) = -sin(u).

Pythagorean Identities

Identities that relate the squares of sine, cosine, and tangent, such as sin²(u) + cos²(u) = 1.

Critical Points

Points on the graph where the derivative is zero or undefined, indicating potential maxima, minima, or points of inflection.

Graphing Function

The process of plotting the values of a function on a coordinate system to visualize its behavior.

Dotted x-axis

A temporary line drawn to help visualize critical points before determining the final position of the x-axis.

Solid x-axis

The final position of the x-axis after determining where it should fall based on the graph's critical points.

Function f(x)

An expression that defines a relationship between an input x and an output, such as f(x) = 4/3 sin(2x).

Reflection

A transformation that flips a graph over a specific axis, often altering the amplitude.

Interval

A range of values on the x-axis over which a function is defined or analyzed.

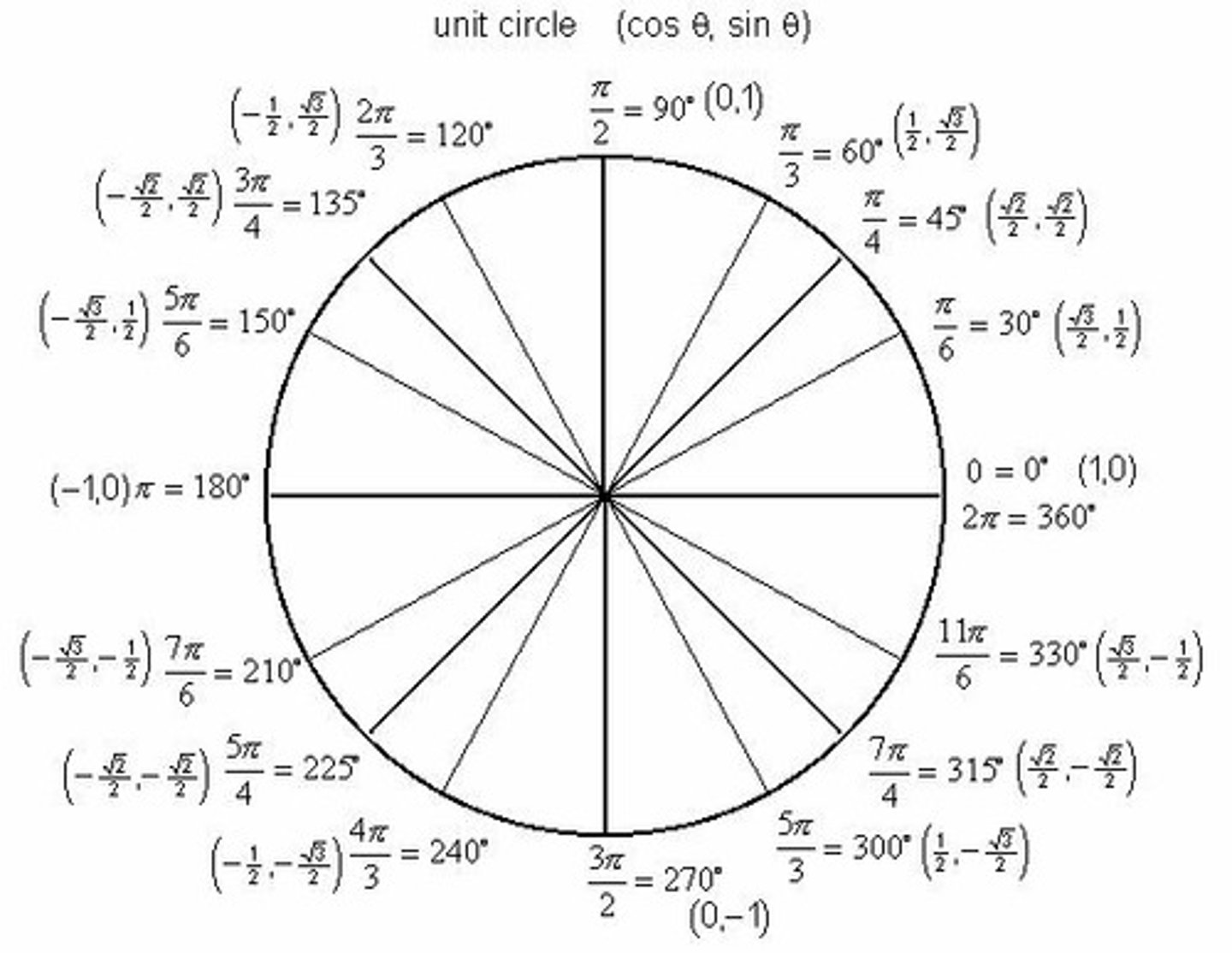
Unit Circle

A circle with a radius of one, centered at the origin of the coordinate plane, used to define trigonometric functions.

SOLUTION

The answer or method used to solve a mathematical problem, often including steps taken to arrive at the answer.

Function's Graph

A visual representation of the relationship between the input and output of a function.

Trigonometric Functions

Functions that relate the angles of a triangle to the lengths of its sides, including sine, cosine, and tangent.

Vertical Shift by 4 units

A transformation of the graph that moves it up 4 units in the y-direction.

Angle Sum Formula for Sine

sin(α + β) = sin(α)cos(β) + cos(α)sin(β)

Angle Difference Formula for Sine

sin(α - β) = sin(α)cos(β) - cos(α)sin(β)

Angle Sum Formula for Cosine

cos(α + β) = cos(α)cos(β) - sin(α)sin(β)

Angle Difference Formula for Cosine

cos(α - β) = cos(α)cos(β) + sin(α)sin(β)

Angle Sum Formula for Tangent

tan(α + β) = (tan(α) + tan(β)) / (1 - tan(α)tan(β))

Angle Difference Formula for Tangent

tan(α - β) = (tan(α) - tan(β)) / (1 + tan(α)tan(β))

Double Angle Formula for Sine

sin(2u) = 2sin(u)cos(u)

Double Angle Formula for Cosine

cos(2u) = cos²(u) - sin²(u)

Double Angle Formula for Tangent

tan(2u) = 2tan(u) / (1 - tan²(u))

Power Reduction Formula for Sine

sin²(x) = (1 - cos(2x)) / 2

Power Reduction Formula for Cosine

cos²(x) = (1 + cos(2x)) / 2

Product to Sum Formula for Sine

sin(α)sin(β) = 1/2 [cos(α - β) - cos(α + β)]

Product to Sum Formula for Cosine

cos(α)cos(β) = 1/2 [cos(α - β) + cos(α + β)]

Sum to Product Formula for Sine

sin(x) + sin(y) = 2sin((x + y)/2)cos((x - y)/2)

Sum to Product Formula for Cosine

cos(x) + cos(y) = 2cos((x + y)/2)cos((x - y)/2)

Trigonometric Equation Example

Solve the equation 3 csc²(x) + 3 = 0 on the interval [0, 2π).

Unit Circle and Sine

Sine is defined by the y-coordinates on the unit circle.

Identifying Angles on Unit Circle

Identify angles where the y-coordinate is -3/2.

Solutions for Trigonometric Equation

The solutions are x = 4π/5 and x = 3π/3.