AQA A-Level Physics: Waves and Optics Concepts

Frequency

The number of waves passing through a point per second. (hertz) Hz

Wavelength

The distance between two adjacent peaks on a wave.

Amplitude

The maximum displacement of the wave from its equilibrium position.

Time period of a wave

T = 1/f

Phase difference

How much a particle / wave lags behind another particle / wave. Measured in radians, degrees or fractions of a cycle.

Longitudinal wave

A wave in which the oscillation of the particles is parallel to the direction of energy transfer. There are rarefactions (areas of low pressure) and compressions (areas of high pressure).

Transverse wave

Waves where the particle oscillations are perpendicular to the direction of energy transfer. For example: electromagnetic waves.

Speed of electromagnetic waves in vacuum

3 x 10^8 m/s

Magnetic and electric fields in electromagnetic waves

False. The electric and magnetic field are at right angles to each other.

Polarising filter

Only allows oscillations in one plane.

Polarisation as evidence of transverse waves

Polarisation can only occur if a wave's oscillations are perpendicular to its direction of travel (as they are in transverse waves).

Polarisation in antennas

TV and radio signals are usually plane-polarised by the orientation of the rods on the transmitting aerial, so the receiving aerial must be aligned in the same plane of polarisation to receive the signal at full strength.

Stationary wave

A wave which transfers no energy and whose positions of maximum and minimum amplitude are constant.

Node

A point on a stationary wave where the displacement is 0.

Antinode

A point on a stationary wave with maximum displacement.

Conditions for stationary wave production

●The waves must be of the same frequency, wavelength and amplitude. ●They must be travelling in opposite directions. These conditions are often met when a wave is reflected back onto itself.

Production of stationary waves

A stationary wave is formed from the superposition of 2 progressive waves, travelling in opposite directions in the same plane, with the same frequency, wavelength and amplitude. ●Where the waves meet in phase, constructive interference occurs so antinodes (regions of maximum amplitude) form. ●Where the waves meet completely out of phase, destructive interference occurs and nodes (regions of no displacement) form.

First harmonic for stationary wave with two closed ends

It consists of 2 nodes at either end and an antinode in the middle.

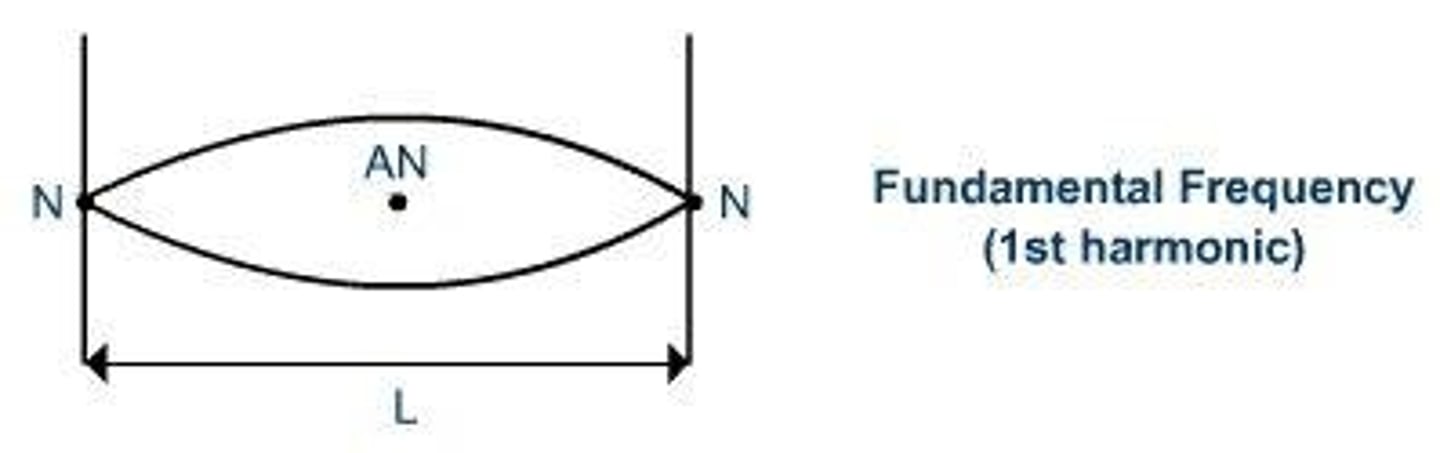
Second harmonic for stationary wave with one open end and one closed end

It consists of two nodes and two antinodes, with one of the nodes at the closed end and one of the antinodes at the open end.

Coherence

Coherent waves have a fixed phase difference and the same frequency and wavelength.

Usefulness of a laser in interference and diffraction

It produces monochromatic (same wavelength / colour) light so diffraction and interference patterns are more defined.

Young's double-slit experiment

A single light source is directed towards two slits, which each act as a coherent light source, the light interferes constructively and destructively to create an interference pattern.

Interference pattern using white light

A bright white central maximum flanked by alternating spectral fringes of decreasing intensity with violet closest to the zero order and red furthest.

Interference pattern through a single slit

The light diffracts as it passes through the slit, where the waves are in phase constructive interference occurs making bright fringes and where the waves are completely out of phase destructive interference occurs making a dark fringe.

Effect of increasing slit width on central diffraction maximum

False, the slit is not so close to the wavelength in size so less diffraction occurs - the central maximum becomes narrower and more intense.

Type of pattern from a single slit

Single Slit.

Approximate refractive index of air

1

Bending of light in a more optically dense medium

Towards the normal.

Total internal reflection occurrence

When light is at a boundary to a less optically dense medium and the angle of incidence is greater than the critical angle.

Purpose of cladding in a step index optical fibre

●Protects core from scratches which would allow light to escape and degrade the signal. ●Allows TIR as it has a lower refractive index than the core.

Effect of signal degradation by absorption in an optical fibre

Part of the signal's energy is absorbed by the fibre so its amplitude is reduced.

Pulse broadening

When the received signal is wider than the original, this can cause overlap of signals leading to information loss.

Cause of pulse broadening by modal dispersion

Modal dispersion causes pulse broadening by different modes traveling at different speeds, leading to signal overlap.

Pulse Broadening

Light rays enter the fibre at different angles so they take different paths along it, causing pulse broadening.

Material Dispersion

When light with different wavelengths is used, some wavelengths slow down more than others in the fibre, causing pulse broadening.

Reduction of Modal Dispersion

Use a single mode fibre (very narrow fibre) so the possible difference in path lengths is smaller.

Reduction of Material Dispersion

Use monochromatic light.

Reduction of Absorption and Dispersion

Use an optical fibre repeater to regenerate the signal now and then.

Advantages of Optical Fibres

Signal can carry more information as light has a high frequency; no energy lost as heat; no electrical interference; cheaper; very fast.

Critical Angle Path

It goes along the boundary ie. the angle of refraction is 90°.

Critical Angle Formula

sinC = n2 / n1 where n1 > n2.

Critical Angle of Water to Air

C = sin^-1 (1 / 1.33) = 48.8°.

Snell's Law of Refraction

n1sini = n2sinr; 1.23sin32 = 1.53sinr; sinr = 1.23sin32 / 1.53; sinr = 0.426; r = 25.2°.

Optical Density Comparison

Glass has a refractive index of 1.5, water has a refractive index of 1.33, thus glass is more optically dense.

Refractive Index Formula

n = c / v where n = refractive index, c = speed of light in vacuum (3x 10^8 m/s), v = speed of light in material.

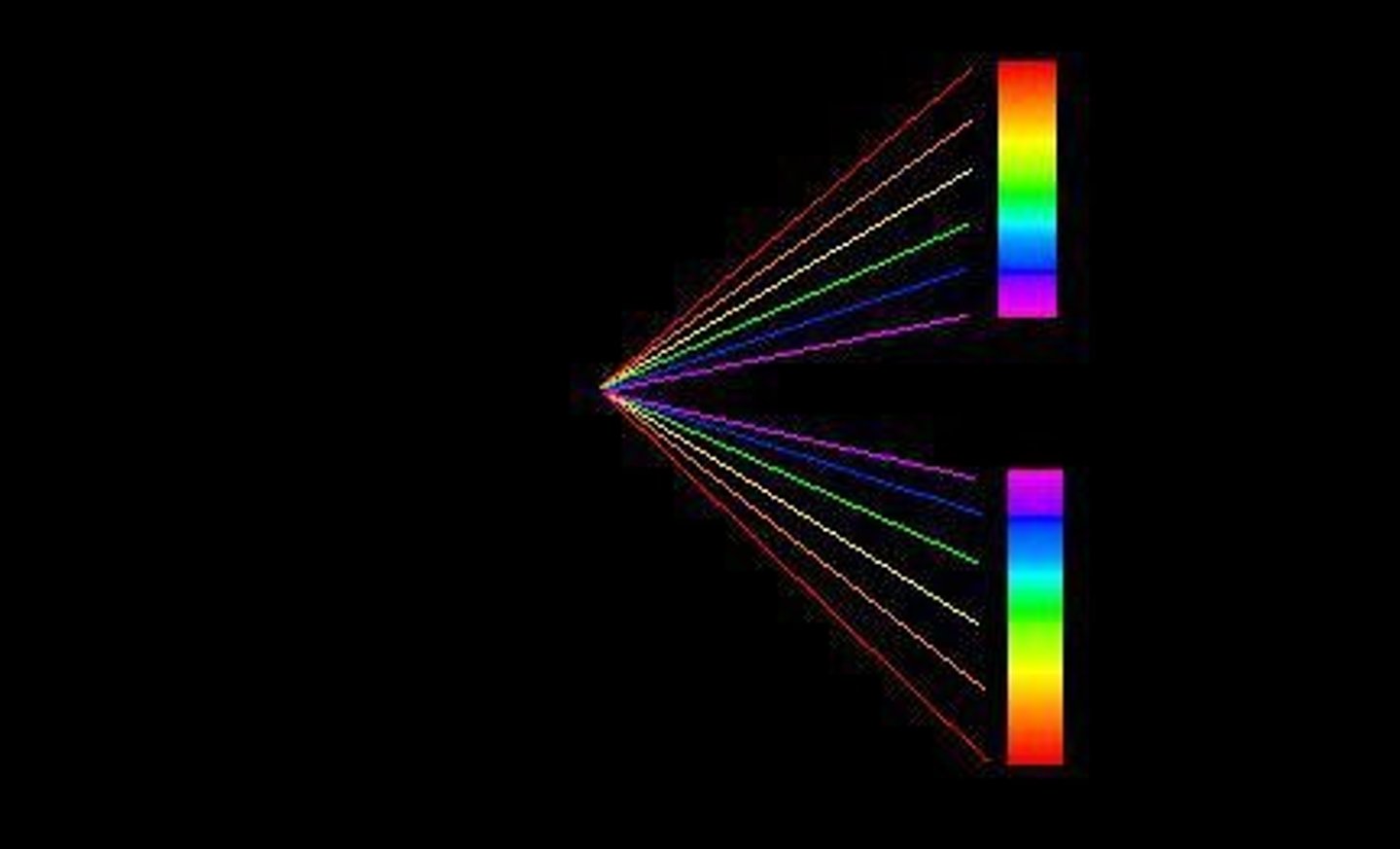
Applications of Diffraction Gratings

Splitting up light from stars to make line absorption spectra; X-ray crystallography, a crystal sheet acts as the diffraction grating the X-rays pass through.

Diffraction Grating Formula

dsinθ = n𝜆.

First order maximum

The path difference between two adjacent rays of light is 1𝜆.

Path difference

The difference in distance travelled by 2 waves.

Diffraction

The spreading out of waves when they pass through or around a gap.

Young's double slit experiment

Provided evidence for the wave nature of light through diffraction and interference patterns.

Safety precautions for lasers

1. Wear laser safety goggles 2. Don't shine the laser at reflective surfaces 3. Display a warning sign 4. Never shine the laser at a person.

Formula associated with Young's double slit experiment

w = λD / s, where w is fringe spacing, λ is wavelength of light used, D is distance from screen to slits, and s is slit separation.

Wavelength calculation

λ = ws / D = (0.04 x 0.2 x 10^-3) / 15 = 5.3 x 10^-7 m.

Investigation of stationary sound waves

Place a speaker at one end of a closed glass tube, lay powder across the bottom of the tube; it will be shaken from the antinodes and settle at the nodes.

Frequency of the first harmonic

T = tension = 2 x 9.81 = 19.62N; μ = mass / unit length = 0.03 / 2 = 0.015 kg/m; f = (¼) x (sqrt: 19.62/0.015) = 9.0 Hz.

Speed of a wave

c = f𝜆; c = (10x10^9) x (6x10^-2) = 6x10^8 m/s.

Phase

The position of a certain point on a wave cycle, with units in radians, degrees or fractions of a cycle.

Interference patterns

False: interference patterns can be formed by sound waves and all EM waves too.

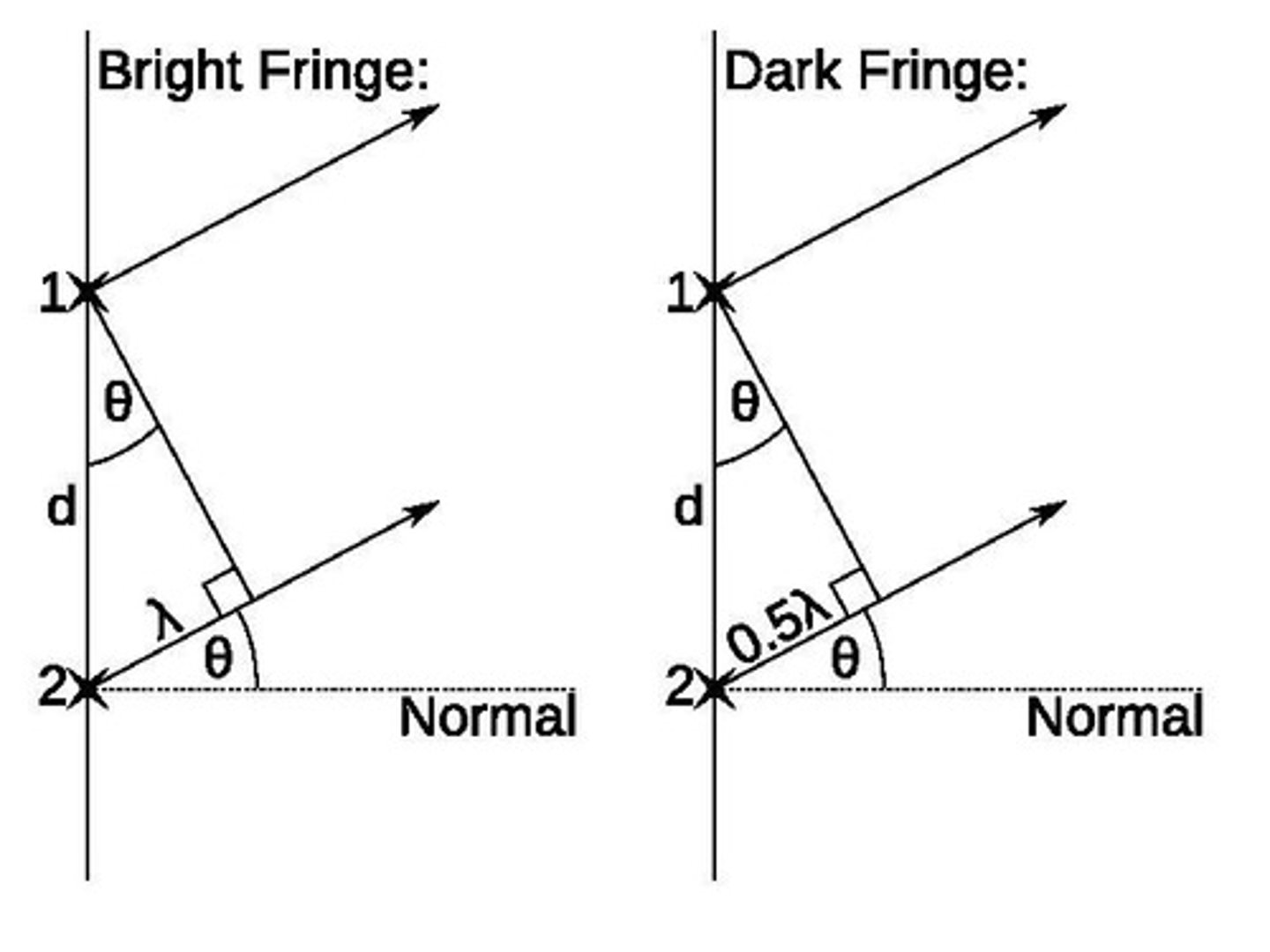
Maxima occurrence condition

Other maxima occur when the path difference between the two rays of light is nλ, where n is an integer.

Triangle in diffraction

A right angled triangle is formed, with side lengths d and λ, where the upper angle is θ.

First maximum condition

For the first maximum, sinθ = λ/d.

Rearranged formula for maximum

Rearranging gives dsinθ = λ.

Effect of wavelength change on diffraction

When light passing through a diffraction grating is changed from blue to red, the orders will become further apart.