discrete math

proposition

a sentence that can only be true or false

¬p

NOT p

p ∧ q

p AND q

p ∨ q

p OR q

p → q

IF p THEN q

p ↔ q

q IF AND ONLY IF p

p ⊕ q

XOR (p or q but not both)

∀x

all x

∃x

at least one x

double negative

¬(¬p) ≡ p

De Morgan’s Laws

NOT acts as distributor for AND and OR

biconditional

p ↔ q ≡ (p → q) ∧ (q → p)

implication flip

p → q ≡ ¬p ∨ q
(if you drink milk, you get sick = either don’t drink milk or you get sick)

sufficient

condition, then q

necessary

q, then condition

converse

if q then p

inverse

if not p then not q

contrapositive

if not q then not p

predicate

sentence with a blank

modus ponens

p → q and p is True, then q is True

modus tollens

p → q, and q is False (¬q), then p is False (¬p)

hypothetical syllogism

p → q and q → r, then p → r

disjunction syllogism

p ∨ q and p is False (¬p), then q is True (q)

addition

if p is True, then p ∨ q is True

simplification

if p ∧ q is True, then p is True and q is True

conjunction

if p = T and q = T, then p∧ q is True

resolution

if p ∨ q and ¬p ∨ r, then q ∨ r

direct proof

given → follow logic → reach the conclusion

contrapositive proof

Prove ¬Q → ¬P instead of P → Q

proof by contradiction

Assume the opposite of what you want to prove → reach a contradiction

vacuous proof

If the premise is false, the implication is automatically true. (ex: “If I’m a potato then I’m a millionaire.”)

trivial proof

If the conclusion is always true, the implication is automatically true. (ex: “If I have five heads, then 1 = 1.”)

Universal Instantiation

Take a general truth and apply it to all.

Universal Generalization

All proofs of something True creates a generalization.

Existential Instantiation

If at least one of something exists, confirm its existence by naming it uniquely.

Existential Generalization

If there’s at least one example of something existing, then one or some exist.

x ∈ A

x is an element of A

x ∉ A

x is not in A

union

A ∪ B (OR)

difference

A − B (elements in A but not B)

intersection

A ∩ B (AND)

complement

A̅ (everything in not A)

cartesian

A × B (pairs of elements)

cardinality

the number of elements in a set (|A|)

bitstring

a string of 1’s and 0’s that are used to represent T and F in a set if numbers (1=T and 0=F)

injective / one-to-one

every input has a different output, no two inputs share the same out put (ex: f(x) = x² doesn’t work because f(-2)=f(2))

surjective / onto

every codomain has to have an x, every f(x) has an x

bijective

a function that is both and injective and surjective

floor function ⌊x⌋

rounds down to the nearest whole number

ceiling function ⌈x⌉

rounds up to the nearest whole number

well-ordering principle

every non-empty set of positive integers has a smallest element

strong induction

a regular induction but for multiple values

mathematical induction

a method to prove a statement is true for all positive integers

1 root closed form

a_n = (C₁ + C₂)(rⁿ)

2 roots closed form

a_n = C₁r₁ⁿ + C₂r₂ⁿ

recursion

when a value depends on previous values

iteration

plugging in values until you see a pattern

combination

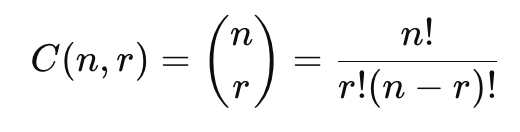
permutation

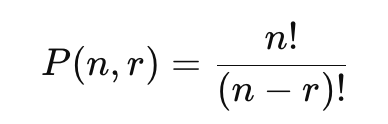
pigeonhole principle

[ N/k ]

binomial theorem

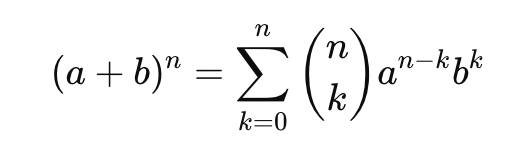
generalized permutations

when you have repeating elements in a set

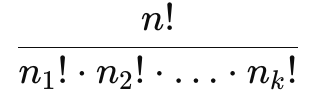
combinations with repetition

when choosing items with replacement and order doesn’t matter

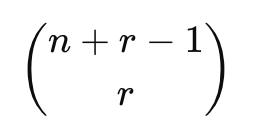
PIE

principles of inclusion and exclusion

PIE for 2 sets

∣A∪B∣=∣A∣+∣B∣−∣A∩B∣

PIE for 3 sets

∣A∪B∪C∣=∣A∣+∣B∣+∣C∣−∣A∩B∣−∣A∩C∣−∣B∩C∣+∣A∩B∩C∣

Baye’s theorem

P(A|B) = (P(B|A) * P(A)) / P(B)

Bernalli’s Theorem

P(k successes) = C(n, k)p^k(1-p)^n-k

independent events

P(A∩B) = P(A) * P(B)

P (A∪B) disjoint

P(A) + P(B)

P (A∪B) overlap

P(A) + P(B) - P(A∩B)

conditional probability

P(A∩B) / P(B)