AP Calculus AB Prerequisite Quiz

Slope intercept form for lines

y=mx+b

Point slope form for lines

y-y1 = m(x-x1)

Standard Form for lines

Ax+By=C

Horizontal Line

y = b (slope = 0)

Vertical line

x = a (slope = undefined)

How do the slopes of parallel lines relate?

they’re the same

How do the slopes of perpendicular lines relate?

they have negative reciprocal slopes

Standard form quadratics

y = ax²+bx+c

vertex form quadratics

y=a(x-h)²+k

factored/intercept form quadratics

y=a(x-d)(x-e)

When does a parabola open upward?

when a>0

When does a parabola open downward?

when a<0

Quadratic formula

x = (-b±√b²-4ac)/2a

Describe polynomial end behavior

• when degree is even, both sides point the same way

• when degree is odd, sides point opposite ways

• when leading coefficient is positive, the function is positive (right side up)

• when leading coefficient is negative, the function is negative (right side down)

How to find vertical asymptotes in rational functions?

set denom equal to 0

How to find horizontal asymptotes in rational functions?

• if degree of num < degree of denom then y=0

• if degree of num = degree of denom then y = ratio of leading coefficients

• if degree of num > degree of denom then y= none or slant

x^a times x^b = ?

x^a+b

(xy)^a = ?

x^ay^a

(x^a/x^b) = ?

x^a-b

(x/y)^a = ?

x^a/y^a

x^-a = ?

1/x^a

^a√x^b = ?

x^a/b

what is y = log_ax equal to

a^y=x

log_a(xy) = ?

log_ax + log_ay

log_a(x/y) = ?

log_ax - log_ay

log_a(x^b) = ?

blog_ax

lne = ?
ln1 = ?

lne = 1

ln1 = 0

cscx =

1/sinx

secx =

1/cosx

cotx =

1/tanx

tanx =

sin/cos

cot =

cos/sin

sin²x + cos²x =

1

tan²x + 1 =

sec²x

1 + cot²x =

csc²x

sin(2x) =

2sinxcosx

cos(2x)=

• cos²x-sin²x

• 1-2sinx

• 2cos²x-1

Linear function

y=x

• domain (-∞, ∞)

• range (-∞, ∞)

Quadratic function

• y=x²

• domain (-∞, ∞)

• range [0, ∞)

reciprocal/rational function

• y=(1/x)

• domain (-∞,0)U(0, ∞)

• range (-∞, 0)U(0,∞)

• HA @ y=0

• VA @ x=0

Absolute value function

• y = |x|

• domain (-∞, ∞)

• range [0, ∞)

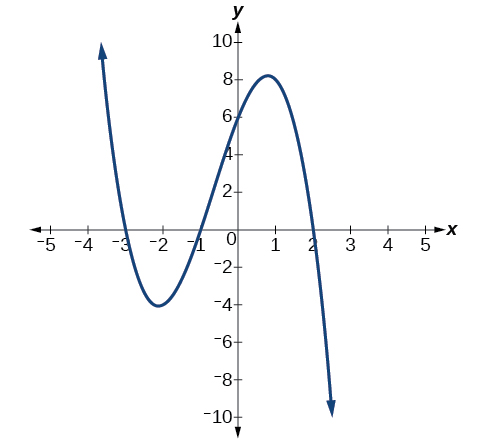
Odd Degree polynomials

• y=xⁿ (where n is odd)

• domain (-∞, ∞)

• range (-∞, ∞)

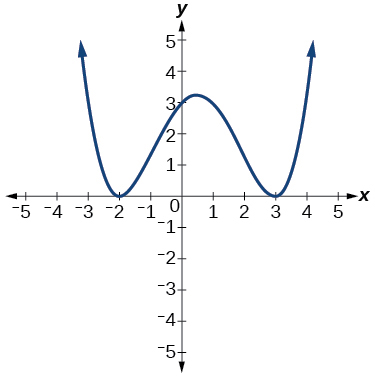
Even degree polynomials

• y=xⁿ (where n is even)

• domain (-∞, ∞)

• range [0, ∞)

Exponential function

• y=a^x

• domain (-∞, ∞)

• range (0, ∞)

• HA @ y=0

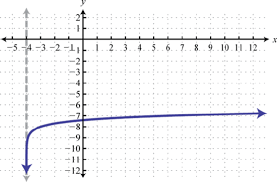
Logarithmic function

• y = log_zx or y = lnx

• domain (0, ∞)

• range (-∞, ∞)

• VA @ x=0

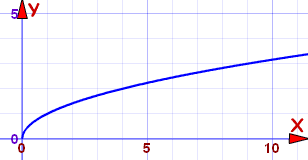
Even root function

• y = ⁿ√x (where n is even >1)

• domain [0, ∞)

• range [0, ∞)

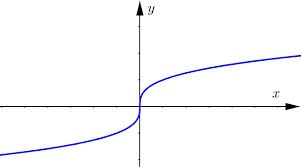
Odd root function

• y = ⁿ√x (where n is odd >1)

• domain (-∞, ∞)

• range (-∞, ∞)

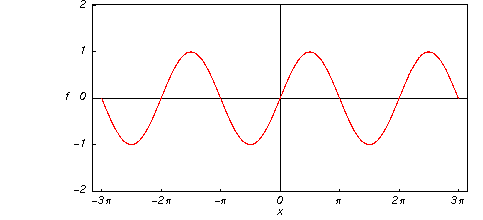
Sinusoidal function

• y=asinx or y=acosx

• domain (-∞, ∞)

• range [-a, a]

Tangent function

• y = tanx

• domain (-pi/2, pi/2)U(((2n+1)∞)/2, ((2n+3)pi)/2)

• range (-∞, ∞)

• VA @ x = (2n+1)pi / 2