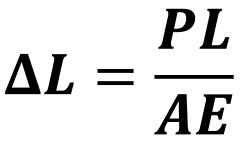SM 143 Stress and Strain

Stress

intensity of internal force acting on specific plane passing through a point

Normal stress & Average Axial/Normal stress σ

intensity of force acting normal to A

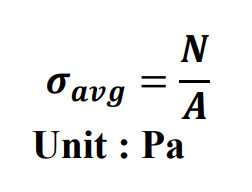
Shear stress & Average shear stress τ

intensity of force acting tangent to A.

Can have single and double shear; number of seperate areas being sheared.

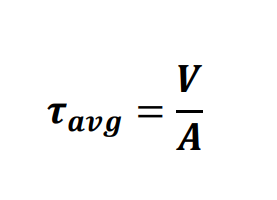
Assumptions

• Bar remains straight

• Deforms uniformly

• Loaded on centroid

Material assumption:

• continuous (no voids) and cohesive (all portions connected – no breaks)

Homogeneous & Isotropic

Material has the same physical and mechanical properties throughout its volume

Material has the same properties in all directions

Strain

the effect/result of force. A measure of deformation.

Normal strain ε

result of normal forces (change in volume)

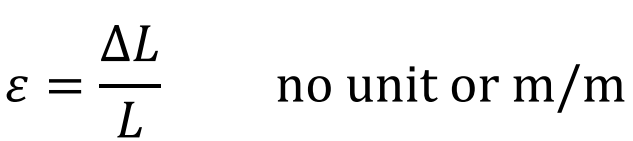
Shear strain γ

result of shear forces (change in shape/angle).

Increase in γ is negative & decrease in γ is positive.

• For small angles: tanγ ≈ γ

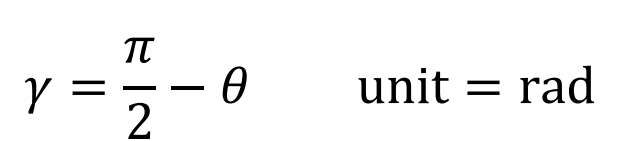
Hooke’s Law

σ = Eε, E is Young’s modulus.

Only applies to elastic region or for elastic deformation of material.

Poisson’s ratio

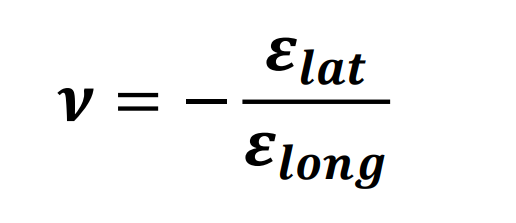
Shear stress-strain ratio

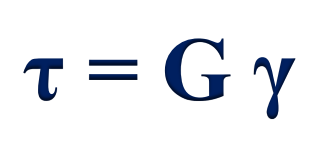
Shear modulus

v is Poisson’s ratio

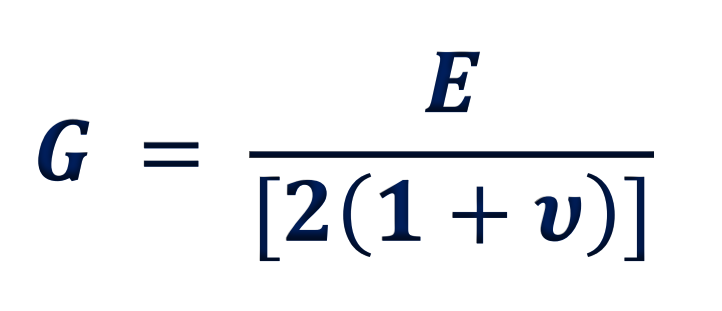
Saint-Venant’s principle

Local deformation & stress concentrations occur where load is applied. Move far enough away from load, effect starts to disappear

Change in axial length

P - internal axial force, L - element length, A - cross-sectional area, E - Young’s modulus.

Tensile Stress is +, deformation caused by tensile stress is +, therefore lengthening is +.

Formula derived from Hooke’s Law.