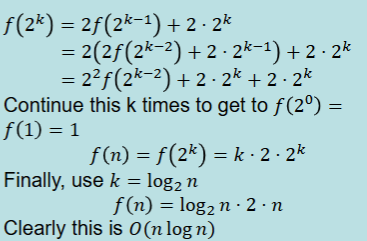Sorting and Algorithm Complexity - Week 3

Examples of Complexity for O(1)

→ Adding to an array
→ Stacks (push/pop)
→ Queues (enqueue/dequeue)
→ Deleting from linked list

Examples of Complexity for O(n)

→ Search in an array
→ Adding to an ordered array
→ Search in stack or queue
→ Search in a linked list

What are the resources code consumes when running, and what should we use to measure performance in terms of resources running?

The resources consumed are hardware, memory and time.
We should try to measure:

→ Space (equivalent to memory or hardware resources)

→ Time

What do we grade the difficulty of an algorithms inputs by? Give an example:

The size

e.g. Searching a list takes time depending on the lists length

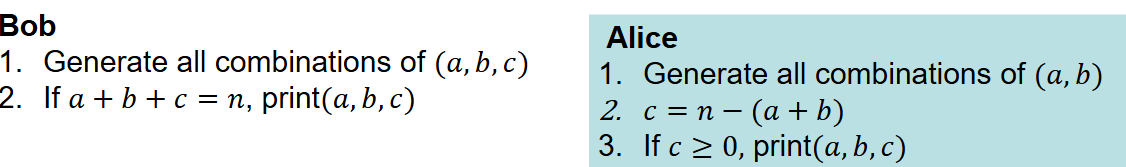
Using Bob and Alice’s algorithm for finding all non-negative integers (a,b,c) such that a+b+c=n. What are both of the complexities?

Bob: Each variable can take n+1 values, so the complexity is:
f_b(n) = (n+1)³ = n³ + 3n² + 3n + 1

Alice: Each variable can take n+1 values, so the complexity is:
f_a(n) = (n+1)² = n² + 2n + 1

Using Bob and Alice’s algorithm, who’s grows faster and why?

Bob’s grows quicker, because n³ > n²

This is the intuitive idea of Big-O notation.

Formal definition of O(g)

Give functions f, g ℕ → ℕ, f is of order g if there is positive integers c and n₀ such:
f(n) =< cg(n) for all n >= n₀

The set of all functions order g is denoted by O(g)

Define the order for:

f(n) = n³ + 3n² + 3n + 1

n³ + 3n² + 3n + 1 =< n³ + 3n³ + 3n³ + 1n³ =< 8n³

f(n) =< cn³ where c = 8 and n₀ = 1, so f(n) ∈ O(n³)

Definition of Ω and Θ

We can define f ∈ Ω(g) if there exists positive integers c and n₀ such, f(n) >= cg(n) for all n_0.

f grows no slower than g (Big Ω lower bound)

If f ∈ O(g) and f ∈ Ω(g) then f ∈ Θ(g) and g∈ Θ(f) , f and g grow at the same rate.

Simple Big-O notation:
O(1)
O(log_an)
O(n)
O(nlogn)
O(n²)
O(eⁿ)
O(n!)

Constaint
Logarithmic, n > 1
Linear
n log n: linearithmic
Quadratic
Exponential
Factorial

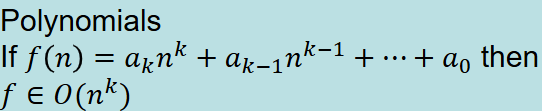
Polynomials (big-o notation):

The order is the largest power, the
multiplying constant does not matter

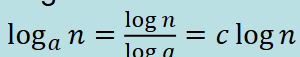
Logs (big-o notation):

And since multiplying constants does not matter:

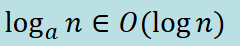
Give the process of designing an algorithm using invariants:

Idea: Iterate, and, at each operation, maintain some property of the data (the invariant). At the start, the input has the property, and at the end, the output has the property.

Sorting invariant → At iteration k, the list 0….k-1 is sorted.
At starting elements → 0..0 is sorted.
At end elements → 0…(n-1) is sorted (everything)

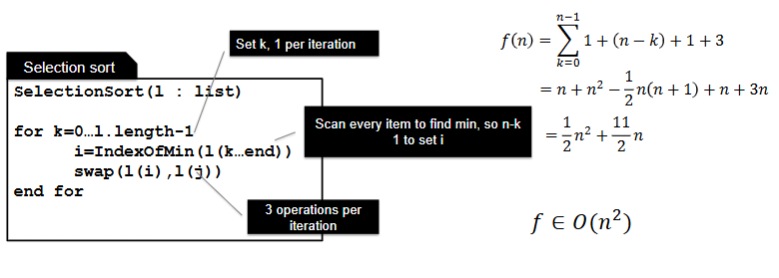
For this problem, write the pseudocode for a selection sort and explain the process:

In the loop body, we put instructions to
maintain the invariant.
At the start of iteration k, we are sorted
up to k-1.
After iteration k, we should be sorted up
to k.
Need to find the element in position k
This will be the smallest element left
Then move it into position

What is the size of the input for this algorithm:

The length of the list, n = l.length

For this algorithm, what is the types of input for the best case?

List already in order

No swaps necessary, checked in linear time

Unrealistic and not informative

For this algorithm, what is the types of input for the average case?

Maybe, but need to analyse all cases

Need to know probability of different inputs

For this algorithm, what is the types of inputs for the worst case?

Gives an upper bound on the run time

Very useful analysis

What is time complexity?

The time taken to run the worst case of a list of length n

For this algorithm, calculate the number of steps

What is the idea behind divide-and-conquer?

Divide the list into two equal parts, and sort each seperately. Merge the result.

Write the algorithm for a merge sort

For this algorithm, do the complexity analysis:

So f(n) = 2f(n/2) + 2n +2. simplifications → 2n
List length is exactly a power of 2, n = 2^k