Bioestadística, R pearson

¿Qué es una variable cualitativa y cuál es un ejemplo de ella?

Una variable cualitativa expresa cualidades, características o atributos que solo pueden clasificarse por conteo. Ejemplo: Sexo (masculino/femenino).

Mencione las cuatro escalas de medición y dé un ejemplo de cada una.

• Nominal: Clasifica sin orden (ej. Grupo sanguíneo).

• Ordinal: Ordena categorías (ej. Grado militar: General, Capitán).

• Intervalo: Distancias iguales entre valores, cero arbitrario (ej. Temperatura en °C).

• Razón: Cero absoluto (ej. Peso en kg).

Escriba la fórmula para calcular la media en una serie agrupada.

¿Qué es la bioestadística y cuál es su importancia en la salud pública?

La bioestadística es la aplicación de métodos estadísticos en el campo de la biología y la medicina. Su importancia radica en que permite recolectar, analizar e interpretar datos para tomar decisiones basadas en evidencia, como evaluar tratamientos, estudiar epidemias o medir la eficacia de políticas sanitarias.

¿Cuál es la diferencia entre datos cualitativos y cuantitativos? Dé un ejemplo de cada uno.

• Cualitativos: Describen atributos o categorías (ej. Estado civil, grupo sanguíneo).

• Cuantitativos: Se expresan numéricamente y pueden medirse (ej. Edad, peso, talla).

Defina "población" y "muestra" en investigación estadística.

• Población: Conjunto completo de individuos o elementos de interés en un estudio (ej. Todos los pacientes con diabetes en un país).

• Muestra: Subconjunto representativo de la población, usado para inferir características del grupo mayor.

¿Qué información proporcionan la media, la mediana y la moda?

• Media (promedio): Valor central basado en la suma de datos.

• Mediana: Valor que divide la serie en dos partes iguales (50% arriba y abajo).

• Moda: Valor más frecuente en un conjunto de datos.

¿Para qué sirven la amplitud y la desviación estándar?

• Amplitud: Diferencia entre el valor máximo y mínimo (indica el rango de los datos).

• Desviación estándar: Mide qué tan dispersos están los datos con respecto a la media.

Describa las características de la curva normal (campana de Gauss).

1. Simétrica alrededor de la media (μμ).

2. Media = Mediana = Moda.

3. 68% de los datos están dentro de μ±σμ±σ, 95% en μ±2σμ±2σ, y 99.7% en μ±3σμ±3σ.

4. El área total bajo la curva es 1 (100%).

¿Qué mide el coeficiente de correlación de Pearson (rr)?

Mide la relación lineal entre dos variables cuantitativas (de intervalo o razón). Indica la dirección (positiva/negativa) y la fuerza (de -1 a +1) de la asociación, sin implicar causalidad.

¿Qué tipo de hipótesis prueba el coeficiente de Pearson?

Hipótesis correlacional, por ejemplo: "A mayor X, mayor Y" o "A mayor X, menor Y". No prueba causalidad.

Mencione dos condiciones necesarias para aplicar el coeficiente de Pearson.

1. Las variables deben ser cuantitativas (intervalo o razón).

2. La relación entre las variables debe ser lineal (verificable con un diagrama de dispersión).

¿Por qué un r=0.10r=0.10 se considera una correlación débil?

Porque la magnitud de la asociación es cercana a cero, lo que sugiere que casi no hay relación lineal entre las variables.

Escriba la fórmula del coeficiente de Pearson.

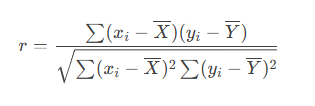
Si r=0.90r=0.90 entre horas de estudio y calificaciones, ¿se puede concluir que estudiar más causa mejores notas?

No. Pearson solo muestra asociación. Podría haber otros factores (ej. motivación) influyendo. Se requieren estudios experimentales para probar causalidad.

¿Cómo usaría Pearson en un estudio médico?

• Presión arterial y edad.

• Nivel de colesterol y peso.
  Los resultados ayudan a identificar factores de riesgo, pero no determinan causas.

¿Qué hace único al coeficiente de Pearson?

• Mide solo relaciones lineales: No detecta patrones no lineales (ej. U-shaped).

• Sensible a valores atípicos (outliers): Un solo dato extremo puede distorsionar rr.

• Ejemplo: Si en un estudio de peso y talla hay un paciente con obesidad mórbida, rr podría sobreestimarse.

¿Cómo verificar si Pearson es aplicable?

1. Diagrama de dispersión: Confirmar que los puntos siguen una tendencia lineal.

2. Normalidad: Idealmente, ambas variables deben distribuirse normalmente (usar pruebas como Shapiro-Wilk).

3. Homocedasticidad: La variabilidad de los datos debe ser constante a lo largo de la relación.