Discrete Math

How many permutations of the letters ABCDEFGH contain

a. The string ED?

b. The Strings CAB and BED?

A coin is flipped 10 times where each flip comes up either heads or tails. How many possible outcomes

a. Are there in total

b. Contain at least three heads

c. Contain the same number of heads and tails

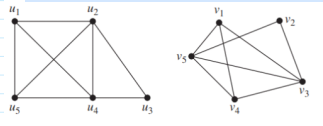
Determine whether the given pair of graphs is isomorphic. If so, show the isomorphic function.

Find the solution to this recurrence relations with the given initial conditions

a_n = 2a_n-1 − 3, a₀ = −1

Find the solution to this recurrence relations with the given initial conditions

a_n = 2a_n-1 + n , a₀ = 1

Suppose that a department contains 10 men and 15 women. How many ways are there to form a committee

with six members if it must have more women than men?

Find the solution to this recurrence relations with the given initial conditions

a_n = 2na_n-1 , a₀ = 1

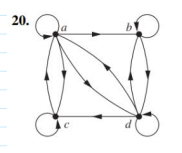
Determine if the graph is bipartite

Find the solution to this recurrence relations with the given initial conditions

a_n + 2 = -4a_n+1 + 5a_n for n >= 0, a₀ = 2, a₁ = 8

Find the solution to this recurrence relations with the given initial conditions

a_n = 5a_n-2 - 4a_n-4

a₀ = 3, a₁ = 2, a₂ = 6, a₃ = 8

Find the solution to this recurrence relations with the given initial conditions

a_n = a_n-2 for n >= 2, a₀ = 5, a₁ = -1

Show that in a simple graph with at least two vertices there must be two vertices that have the same degree.

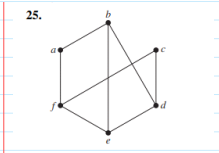
Determine if the graph is bipartite

Let G be a graph with v vertices and e edges. Let M be the maximum degree of the vertices of G, and let m be the minimum degree of the vertices of G. Show that

a. 2e/v >= m

b. 2e/v <= M

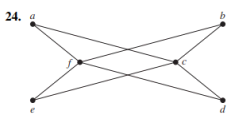
Find the adjacency matric of the given multigraph with respect to the vertices listed in alphabetic order

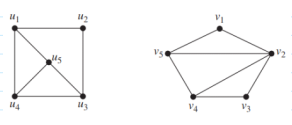
Determine whether the given pair of graphs is isomorphic. If so, show the isomorphic function.

Show that in every simple graph there is a path from every vertex of odd degree to some other vertex of odd degree

Are the following expressions ¬p → (q → r) and q → (p ∨ r) logically equivalent?

True

Determine the truth value of the statement
∃w ∀b (b⁶ > w)
if the domain of the variables consists of positive (non-zero) real numbers.

Prove: For every integer a > 0: If a is irrational then a^1/7 is irrational

Prove that: (2/3) * 4^1/3- 6 is an irrational number

Provide the best big-O estimate for

(n⁴+n²log²⁵n)(15⁴⁰⁰log¹²⁶n+n) + (n! + 56n⁴⁵⁶⁶)(163ⁿ + 78n²log¹²⁹n)

Suppose a password for a computer system must have at least 7, but no more than 11 characters where each character in the password is a lower case letter, upper case letter, binary digit, or one of 7 special characters (*, >, <, !, +, =, $})
How many of these passwords contain at least 1 occurrence of at least 1 of the 7 special characters?

How many functions are there from a set {1, 2, 3, …., n} to the set {x, y} that assign y to both 1 and n?

Prove that 8 (exactly) divides: 3^4k+1 + 5^2k+1

Prove that 35ⁿ is not O(34ⁿ), where n is the size of the input

Let y, x and we be a positive integer:

Prove that among any group of 1+yxw integers, there are at least (xy + 1) with exactly the same remainder when they are divided by w.

Let x > 0. Prove: If 24/x⁵ is irrational, then x^1/19 is irrational.

Prove that: (23/34) * 4^1/3 - 26 is an irrational number.

Let h be a function from set T to set S.
Let A and B be subsets of T.

Prove that: h(B) ∪ h(A) ⊂ h(A ∪ B)

Suppose a password for a computer system must have at least 7, but no more than 11 characters, where each character in the password is a lower case English letter, an upper case English letter, a binary digit, or one of the seven special characters (*, >, <, !, +, =, $).

How many of these passwords contain at least one occurrence of at least one of the seven special characters.

There are 6 different candidates for governor of a state. In how many different orders can the names be printed on a ballot?

The number of different orders is calculated by finding the factorial of the number of candidates, which is 6! = 720. Or P(6,6)

How many subsets with an odd # of elements does a set with 10 elements have?

C(10, 1) + C(10, 3) + C(10, 5) + C(10, 7) + C(10, 9)

A coin is flipped 10 times. How many possible outcomes

a. Are there in total

b. Contain exactly 2 heads

c. Contains at most 3 heads

d. Contain an equal # of heads and tails

a. 2¹⁰

b. C(10, 2)

c. C(10, 0) + C(10, 1) + C(10, 2) + C(10, 3)

d. C(10, 5)

How many permutations of the letters ABCDEFGH contain

a. ED

b. CDE

c. BA and FGH

a. P(7, 7)

b. P(6, 6)

c. P(5, 5)

Department has 10 men, 15 woman. How many ways are there to form a group of 6. If it must have an equal # of men and woman?

C(10, 3) * C(15, 3)