Compounding interest & Population growth.

Compound interest, continues growth, Exponential Growth, and Expontential Decay all in one.

What is the compounding interest formula?

A = P(1 + r/n)^nt

What does the A in the compound interest formula (A = P(1 + r/n)^nt) represent?

The future value/amount you will have

What does the P in the compound interest formula (A = P(1 + r/n)^nt) represent?

The amount you started with (The principle)

What does the r in the compound interest formula (A = P(1 + r/n)^nt) represent?

The interest rate. Note: it always comes as a percentage, so you have to divide by 100 first.

What does the n in the compound interest formula (A = P(1 + r/n)^nt) represent?

Number of times it is compounded per year. If its compounded monthly, there are 12 months in a year, so n = 12.

What does the t in the compound interest formula (A = P(1 + r/n)^nt) represent?

The time in years. So for how many years its being compounded for.

If something is compounded Daily what is n equal to?

n = 365, there are 365 days in a year

If something is compounded monthly what is n equal to?

n = 12, There are 12 months in a year

If something is compounded Quarterly what is n equal to?

n = 4, quarter= 1/4.

Also a single quater is 3 months. 12/4 (four quarters) = 3.

If something is compounded Semiannually what is n equal to?

n = 2, 12/6 = 2.

If something is compounded anually what is n equal to?

1, there is 1 year in a year.

Remember: always ____ r (interest rate) by ___, before putting it into the compound interest equation.

divide, 100

Alyssa invested $6,000 in an account paying an interest rate of 3.9% compounded monthly. Assuming no deposits or withdrawals are made, how much money, to the nearest dollar, would be in the account after 18 years?

A = 12093

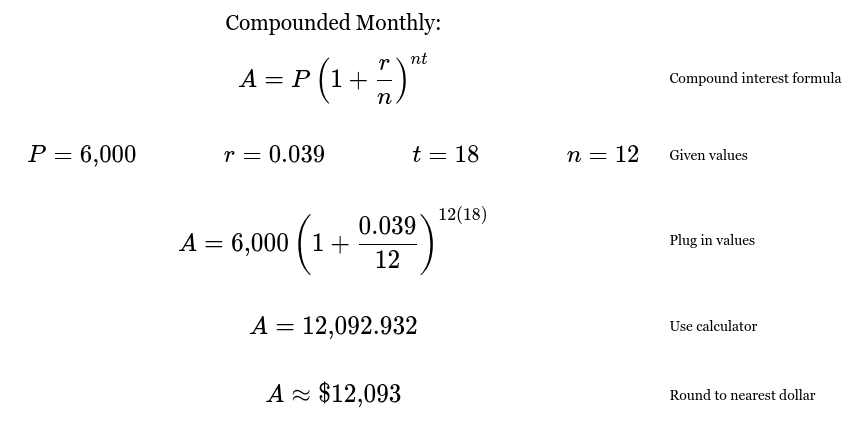
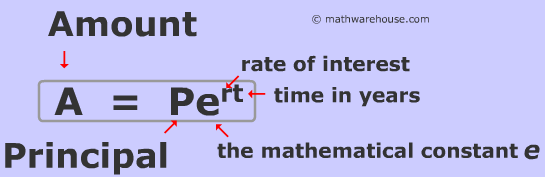
What is the Continuously Compounded Interest formula?

A = Pe^rt

What does the A in A = Pe^rt formula represent?

The amount/ future value

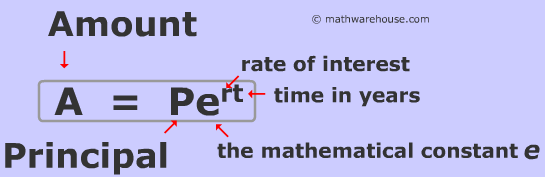
What does the P in A = Pe^rt formula represent?

The initial value (or principle)

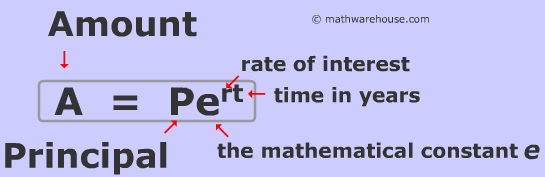
What does the r in A = Pe^rt formula represent?

rate of interest (remember to divide by 100)

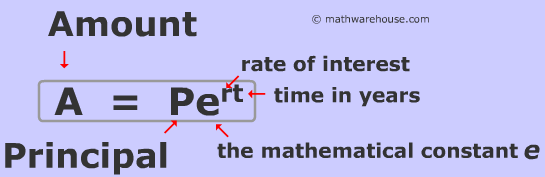
What does the t in A = Pe^rt formula represent?

The time in years (how long its being compounded in years)

Luis invested $62,000 in an account paying an interest rate of 3% compounded continuously. Assuming no deposits or withdrawals are made, how much money, to the nearest dollar, would be in the account after 16 years?

$100197

Omar invested $84,000 in an account paying an interest rate of 6.3% compounded continuously. Assuming no deposits or withdrawals are made, how much money, to the nearest ten dollars, would be in the account after 10 years?

157720

Harper invested $72,000 in an account paying an interest rate of 2% compounded monthly. Assuming no deposits or withdrawals are made, how long would it take, to the nearest tenth of a year, for the value of the account to reach $82,600?

t ≈ 6.9

Josiah invested $96,000 in an account paying an interest rate of 3.5% compounded continuously. Assuming no deposits or withdrawals are made, how long would it take, to the nearest year, for the value of the account to reach $153,400?

t ≈ 13

What does “≈” mean?

Approximately/roughly equal to

Sarah is going to invest in an account paying an interest rate of 6.8% compounded quarterly. How much would Sarah need to invest, to the nearest dollar, for the value of the account to reach $6,500 in 20 years?

P ≈ 1687

Fwam is going to invest in an account paying an interest rate of 5.9% compounded daily. How much would Fwam need to invest, to the nearest hundred dollars, for the value of the account to reach $91,000 in 12 years?

P ≈ 44800

Note: not hundreth but hundred

Naomi is going to invest $78,000 and leave it in an account for 7 years. Assuming the interest is compounded daily, what interest rate, to the nearest hundredth of a percent, would be required in order for Naomi to end up with $91,000?

r ≈ 2.20%

What is the formula for exponential growth?

y = a(1 + r)^t

What is the formula for exponential decay?

y = a(1 - r)^t

What does the y stand for in the exponential growth/decay formula?

y = a(1 ± r)^t

The final amount

What does the a stand for in the exponential growth/decay formula?

y = a(1 ± r)^t

The initial amount

What does the r stand for in the exponential growth/decay formula?

y = a(1 ± r)^t

The rate of increase or decrease

What does the t stand for in the exponential growth/decay formula?

y = a(1 ± r)^t

The time passed

In 2005, there were 1000 rabbits on an island. The population grows 8% every year. At this rate how many, how many rabbits will be on the island by 2020?

3172 rabbits will be on the island in 2020.

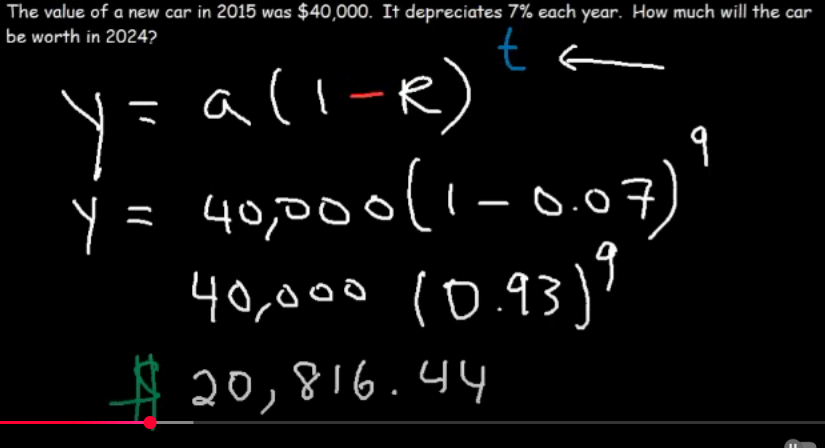
The value of a new car in 2015 was $40,000. It depreciates 7% each year. How much will the car be worth in 2024?

$20,816.44

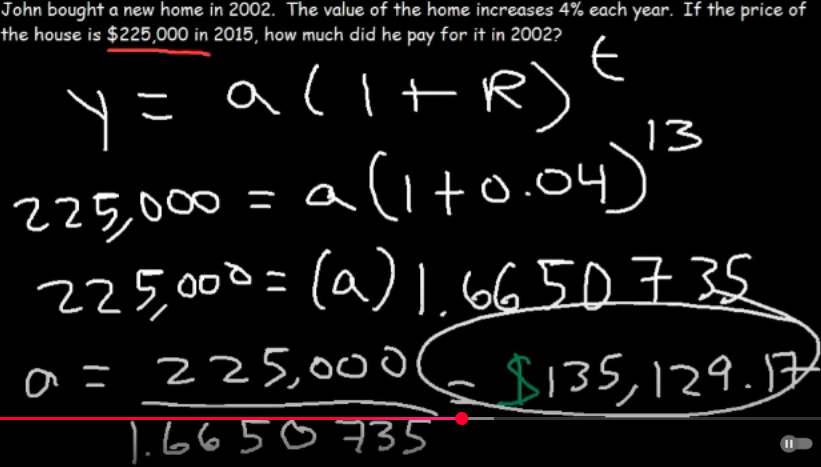
John bought a new home in 2002. The value of the home increases by 4% each year. If the price of the house 225,000 in 2015, how much did he pay for it in 2002? Round to the nearest cent.

$135,129.17

What is the regular growth formula?

y = a(b)^x a is the initial amount and b is what your multiplying it by. t is how many times your multiplying.

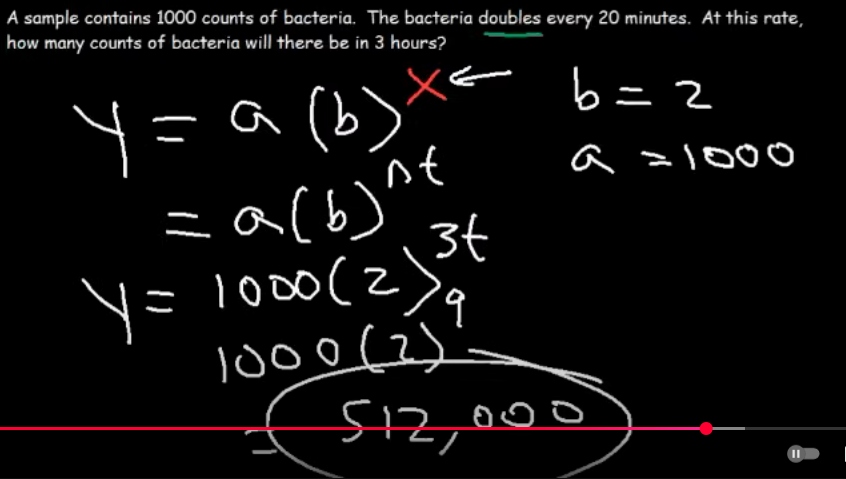
A sample contains 1000 counts of bacteria. The bacteria doubles every 20 minutes. At this rate how many counts of bacteria will there be in 3 hours?

512,000

If you are trying to find the time in a regular growth equation, what equation would you use?

y = a(b)^nt

A sample contains 100 counts of bacteria. The bacteria triples every 15 minutes. How much bacteria will there be in an hour?

8100

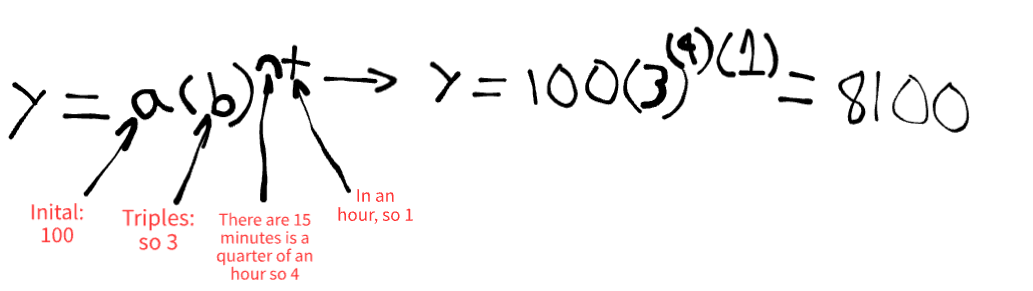
Answer: Skip

Skip