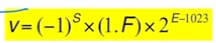COMP 211: Lecture 7 - Integer Overflow and Casting, Bitwise Operations (logic and shift), and Floating Point Representation

What is signed arithmetic overflow?

When 2 signed integers are added, but the result is greater than the max value or less than the min value that can be represented by the number of bits (N).

Example of signed arithmetic flow with 2’s complement (max value)

Answer

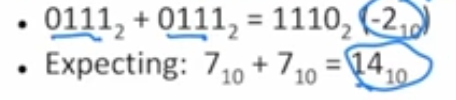
Example of signed arithmetic flow with 2’s complement (min value)

Answer

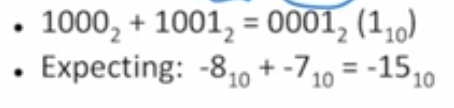
How do we detect arithmetic overflow?

If two positive integers are added, and the result is a negative integer, or if 2 negative integers are added, and the result is a positive number.

0111_2 + 0111_2 = 1110_2 (-2_10)

1000_2 + 1001_2 = 0001_2 (1_10)

What is unsigned arithmetic overflow?

When 2 unsigned integers are added but the result is greater than the maximum value that can be represented by the number of bits (N).

Unsigned arithmetic overflow example (max)

Answer

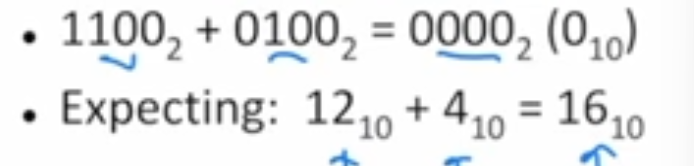
How do we detect unsigned arithmetic overflow?

If the MSB carry-out is 1, then overflow has occurred.

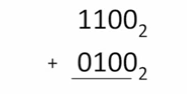
Unsigned arithmetic overflow detection example

Answer

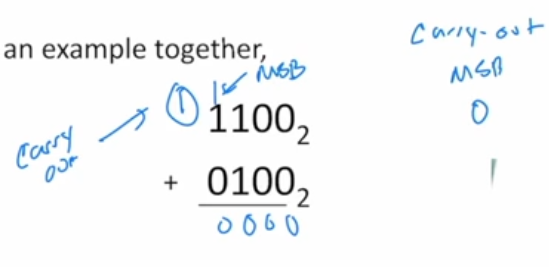
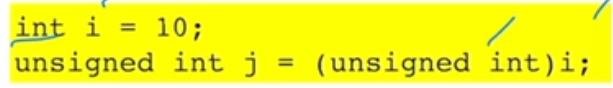
Explain the picture.

i is a signed integer. If we cast it,just changes the interpretation of MSB.

Explain this code.

a is a short variable, which is signed. we cast the short into an unsigned short and put it into variable b. We would expect a 1 to be printed out, but 65535 is actually printed. The short data type is 2-byes (16 bits), and the 2’s complement signed integer -1_10 is 0xFFFF. The Fs represent 1111 1111 1111 1111, and since we only change the interpretation of the MSB, it now represents a positive, not negative number. When we cast an unsigned short, it becomes the maximum positive value for an n=16 bit signed integer (2^16 - 1) = 65535

Binary example of Casting

If we cast it to an unsigned binary number, the MSB not interpreted as a negative number anymore, so it will turn into a positive number. If we go the opposite way, the same thing happens

What is a common mistake for conversion?

Converting a negative integer into a positive integer by performing an unsigned cast operation. If the integer is in 2’s complement, we can’t change the MSB to the opposite number.

How do we do absolute value in 2’s complement?

Using the abs() function in the stdlib library when data type is a signed inter value, or fabs() func in the math library when the data type is a floating point value.

Casting Up

Casting Down

What is the syntax for the bitwise left shift operation?

x « y

How do we do the bitwise left shift operation?

shift x to the left by y bit positions, throw away extra bits on the left, and pad with 0s on the right

What is the left shift always?

logical

How would we do x«3 on 01100010?

00010000

What is the syntax for the bitwise right shift operation?

x»y

How do we do the bitwise right shift operation?

shift x to the right by positions, throw away extra bits on the right

How do we do the bitwise logical right shift operation?

We pad with 0s on the left.

When do we do the bitwise logical right shift operation?

If it is an unsigned data-type

How do we do the bitwise arithmetic right shift operation?

Pad with value of MSB on left.

When do we do the bitwise logical right shift operation?

If it is a signed data type.

How do we do x»2 on 10100010 (both logical and arithmetic)?

Answer

What is u « k equivalent to? What type of shift is it?

u * 2^k. It is a logical shift, meaning it does not preserve the sign bit

1. u « 3

2. (u « 5) - (u « 3)

1. u * 8

2. u * 24

What applies to most machines regarding instructions?

Shift and add/sub instructions are faster than a multiply instruction. If the machine supports the instruction, the compiler might generate the code automatically.

What is u » k equivalent to? What type of shift is it

u/2^k. Both logical and arithmetic shifts can be used. Logical shifts don’t preserve the signed bit, but the arithmetic shift does (2’s complement).

What are the bitwise logic operations? What do A and Brepresent in these?

A and B are N-bit signed or unsigned built-in data types.

• A & B (bitwise and)

• A | B (bitwise or)

• ~A (bitwise not)

• A ^ B (bitwise xor)

• ~0×41

• ~0×00

• 0×69 & 0×55

• 0×69 | 0×55

Answers

What are useful applications of ANDing?

ANDing is useful for “masking” or clearing groups of bits.

Demonstrate ANDing use with an example (1)

Answer

Demonstrate ANDing use with an example (2)

Answer

What are useful applications of ORing?

“setting” groups of bits

Demonstrate ORing use with an example

Answer

What are useful applications of XORing?

“complementing” groups of bits

Demonstrate XORing use with an example

Answer

What is base-10 good for?

Representing non repeating fractions

Demonstrate how we represent this in base-10.

Ans

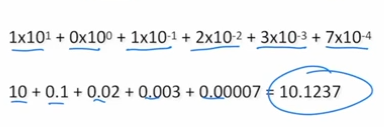
Can we represent repeating fractions in base-10?

Yes, but not perfectly. It requires an infinite number of digits, which isn.t ideal for computers that have a finite amount of memory (RAM).

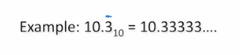
Demonstrate how we represent this in base-10.

Ans

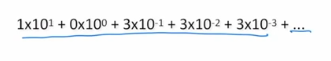
How do we represent fractions in base-2?

Fixed-point representation.

How well can we represent fractions in base-2?

We can “perfectly” represent fractions that are divisible by 2.

Demonstrate how we represent this in base-2.

how can we convert base-10 fractions to base-2?

Ans

Convert .125_10 to base-2

Convert .703125_10 5o base-2

Ans

What are fractions that aren’t a power of 2?

They are likely binary repeating patterns

Can we represent fractions that aren’t a power of 2 in binary?

Yes, but not exactly. Like the base-10 case, it requires an infinite number of digits, and isn’t ideal for computers that have a finte amount of memory.

Example of representing power of 2 in binary

Should we represent fractions that aren’t a power of 2 in binary?

In some cases, yes, because we can close enough to the number we need. In other cases, like many scientific applications, it can be catastrophic. If, for example, some application needed 1000 decimal places of error, that may not be possible to achieve for a particular computing system.

In general, an acceptable precision error is specified by some number of decimal places.

Can signed fixed-point fractions be represented?

yes

Signed magnitude fraction example

Ans

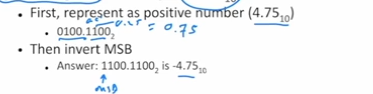
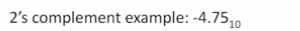
2’s complement fraction example

What is the problem with a fixed-point representation of fractions?

Not a realistic solution. It’s difficult to tell the machine where the location of the decimal point is. Fixed also means that it is unable to be changed, so only a certain number of decimal places are allowed.

What is the solution to the fixed-point representation?

Floating-point representation.

What do we have in floating-point representation?

(sign) (significand) x 2^(exponent

Explain each part of floating-point representation

What representation do computers use? How many and what are the formats?

IEEE 754 floating point representation. It has 2 formats; single and double precision formats.

How many bits can we use in single precision?

Up to 32

How do we divide the bits in a single precision up?

1 bit is for the sign, 8 are for the exponent field, and the last 23 are for the fraction field.

Explain the sign field in single precision.

• It is 1 bit, with 0 = + and 1 = -

• It is in signed magnitude and not in 2’s complement

Explain the exponent field in single precision.

• It has 8 bits, with exponent + 127

• Has bias notation (bias = 127) which means that the power of 2 can represent 2^-127 - 2^127

Explain the fraction field in single precision.

23 bits significand without the leading “1.” that is hidden (normalized).

What is the formula for converting base-10 to IEEE 754 single precision number?

Convert 10.125_10 to IEEE 754 Single precision number

Convert .125_10 to IEEE 754 Single precision number

Ans

What is the difference between single and double precision format?

Double precision has 64 bits while single has 32 bits.

Explain the fields of double precision format.

• Sign field has 1 bit, 0 = +, 1 = -, signed magnitude and not 2’s complement

• exponent field has 11 bits (exponent + 1023), and has biased notation (bias = 1023)

• fraction field has 52 bits significand without the leading 1, which is hidden/normalized

What is the formula for converting base-10 to IEEE 754 single precision number?