Boolean Logic

Logic Gates + Boolean Algebra + Algebraic Expressions + Adders + D-Type Flip Flops + Simplifying Boolean Expressions + De Morgan's Law

Define Boolean Algebra

Logical calculus of truth tables

• developed by George Boole (late 1830s)

• resembles algebra of real numbers but with numeric operations of: multiplication, addition and negation

• variables cam either be TRUE or FALSE (1s & 0s / 5v & 0v)

what is a logic gate

circuits which take boolean inputs and convert them to boolean output

• and

• or

• not

• nand

• nor

• xor

• xnor

drawing truth tables: TRICK

n inputs = 2ⁿ lines in truth table

e.g. 3 inputs = 2³ = 8 lines in truth table

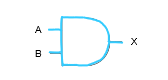
Draw the symbol, algebraic representation and truth table for the AND gate:

• A.B

• 0.0 = 0

• 0.1 = 0

• 1.0 = 0

• 1.1 = 1

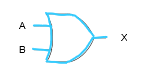
Draw the symbol, algebraic representation and truth table for the OR gate:

• A+B

• 0+0 = 0

• 0+1 = 1

• 1+0 = 1

• 1 +1 = 1

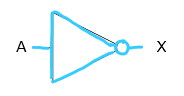
Draw the symbol, algebraic representation and truth table for the NOT gate:

• A with a dash on top

• NOT 0 = 1

• NOT 1 = 0

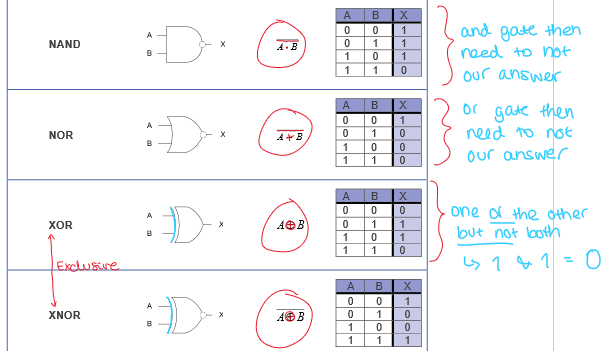
draw the symbol, algebraic representation and truth table for NAND, NOR, XOR, XNOR gates:

Why do we want to reduce the number of gates in our algebraic representation?

Processor needs to be as small & energy efficient as possible

What is the Order of Precedence for Boolean operators?

Brackets first

NOT second

AND third

OR last

What are the ways we can output binary arithmetic?

• logic gates

• Half-adder

• Full Adder

• D-type flip flops

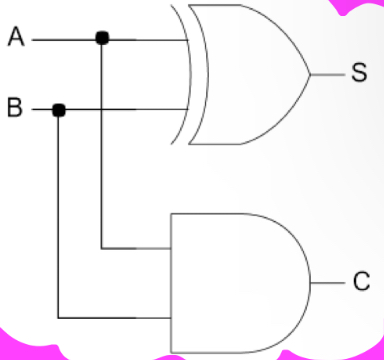
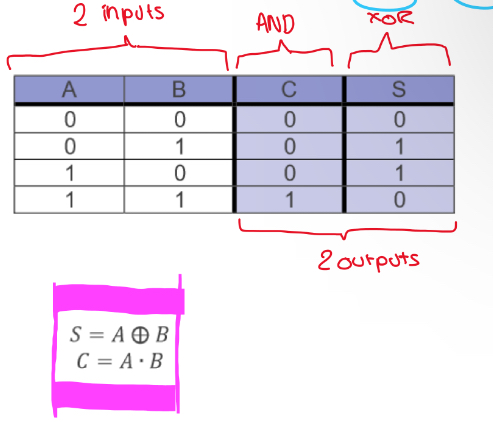
What is a half-adder

Takes 2 inputs & returns two outputs corresponding to the sum & carry when two inputs are added together

What does a half-adder look like?

What does the truth table for a half adder look like?

what does the boolean algabreic equation look like for a half adder

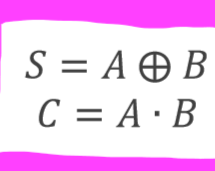
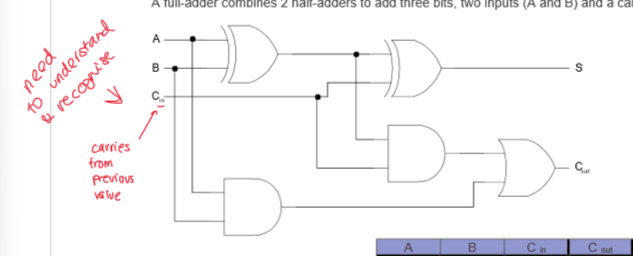
What is a full adder

combines two half adders to add three bits (2 inputs (A & B) and carry a bit (C))

What does a full adder look like?

(dont need to redraw but have to understand and recognise)

what does the truth table for a full adder look like?

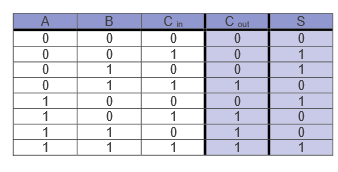
what does the boolean algabreic equation look like for a full adder

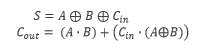
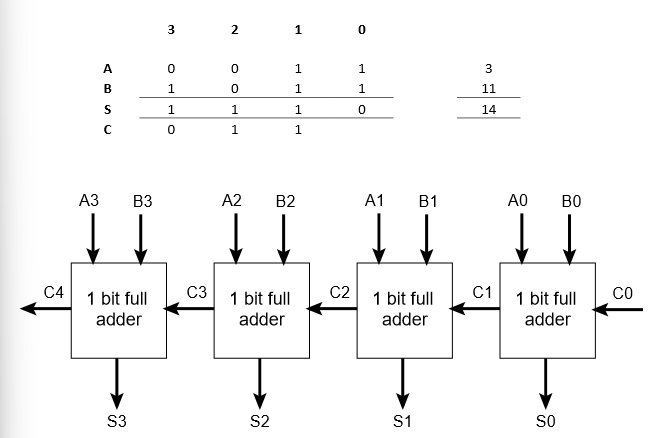
what can full adders be used for

multiple full adders can be connected together to add whole binary numbers together

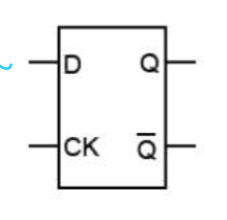
what’s a d- type flip flop?

an elemental sequential logic circuit that stores one bit and flips between two states (0, 1).

how does the d-type flip flop work?

has 2 inputs: D & CK (clock signal)

has 2 outputs: Q & inverse Q

clock signal changes at regular intervals to synchronise the change of state of flip-flop circuit

its effectively 1- bit memory

recursive

keeps data consistent

draw a d-type flip-flop using logic gates:

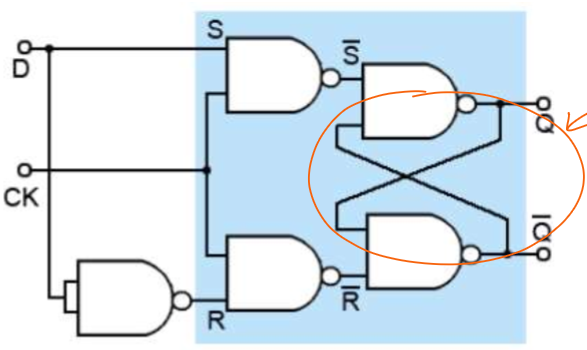
draw the truth table for a d-type flip-flop

X = ‘don’t care‘ state = changes at the D input make no difference to the output as long as the clock input is 0. when CK = 1, there is a change.

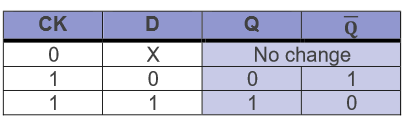
describe what happens in a d-type flip-flop when the CK is high (1):

whichever logic state is at D will appear at output Q. that way you can work out the other output (inverse of Q = opposite of Q)

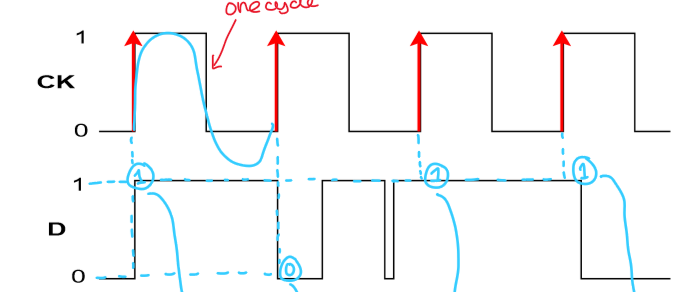
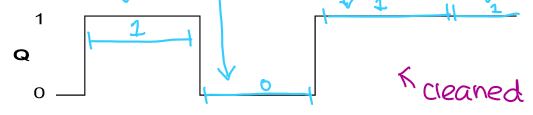
draw this data as cleaned data:

cleaned data has now been outputted for Q to keep data consistent

what is the process of reducing the number of logic gates called and why do we use it?

• minimisation

• improve efficiency - computer can carry out the same task in fewer steps, therefore, reducing time to solve boolean algebra

SIMPLIFYING BOOLEAN EXPRESSIONS:

normal maths rules:

• A + B = B + A

• A . B = B . A

• A + (B + C) = (A + B) + C

• A. (B + C) = A . B + A . C - expanding

• (A + B) . (A + C) = A + (B . C) - factorising

SIMPLIFYING BOOLEAN EXPRESSIONS:

using truth tables

A . A = A

A . 0 = 0

A . 1 = A

A . NOTA = 0

A + A = A

A + 0 = A

A + 1 = 1

A + NOTA = 1

De Morgan’s Law

1. negate individual variables

2. change the operator

3. negate whole expression

advantages of using de morgan’s law

• minimises cost of production

• increases processing speed

• minimises heat generated

• reduces power consumption