AH Maths

Arithmetic Sequence formula

Un= a + (n-1)d

nth term of a geometric sequence

Un = ar^n-1

Inverse of 2×2 matrix

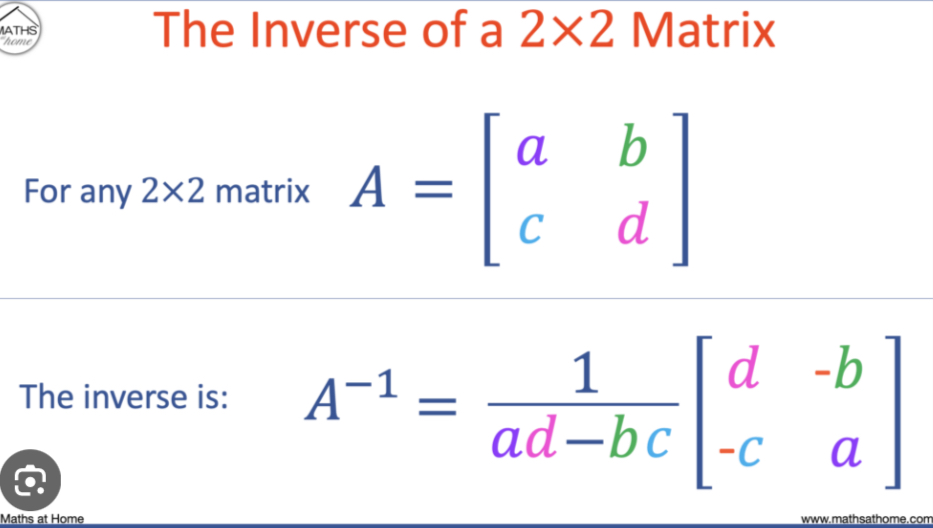
Maclaurin expansion for e^x

1 + x + x² / 2! + x³ / 3! + x^4 / 4!

Maclaurin expansion for sinx

x - x³ / 3! + x^5 / 5! - x^7 / 7! …

Maclaurin expansion for cosx

1 - x² / 2! + x^4 / 4! - x^6 / 6! …

(AB)^-1

A^-1 • B^-1

Sum of infinite geometric series

S=a/1-r

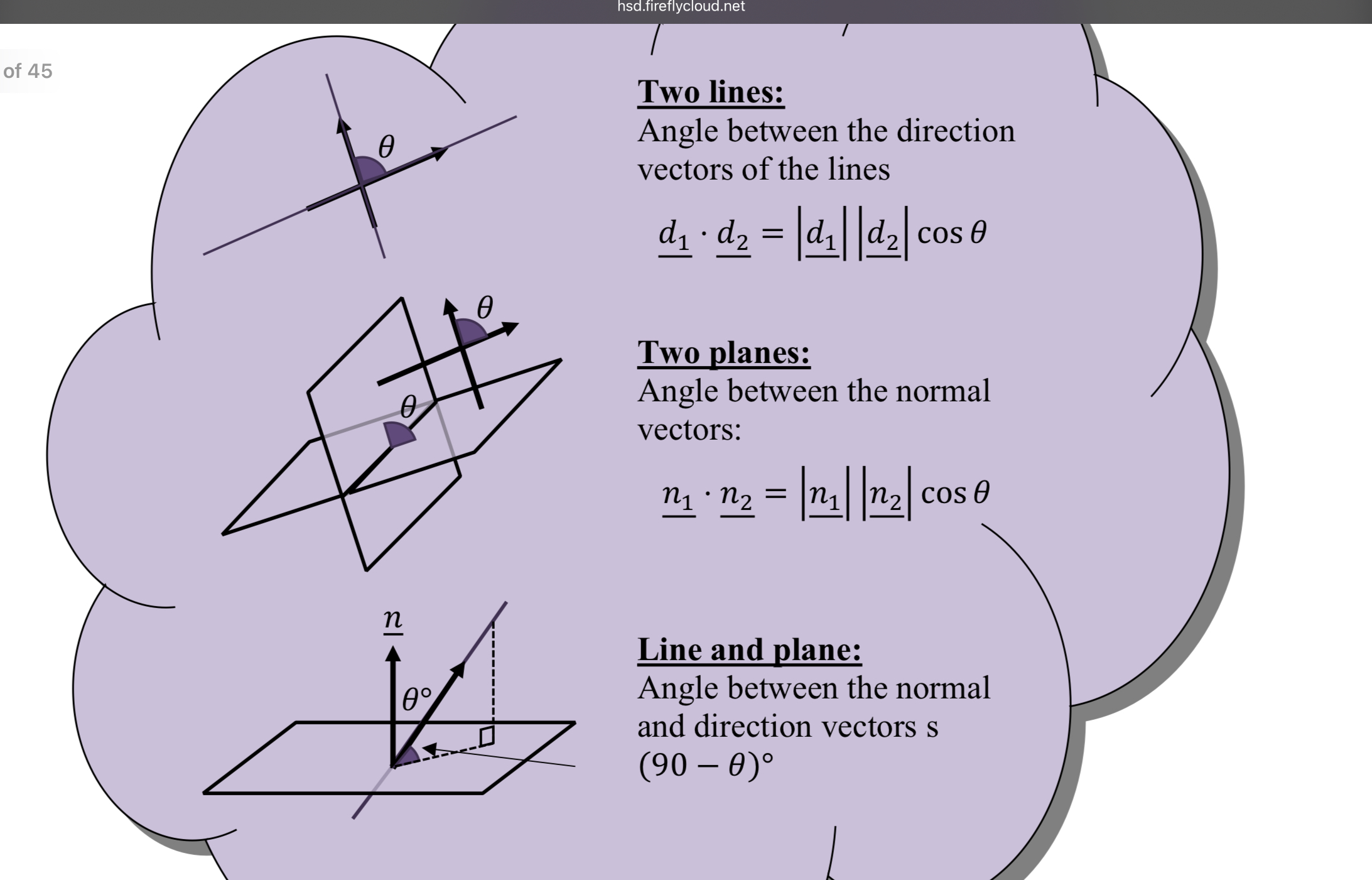
Angle between things

Odd function

f(-x)=-f(x)

Even function

f(-x)=f(x)

2nd derivative of parametric equations

d2y/d2x = d/dt • (dy/dx) • dt/dx

d/dx(f(y)) =

d/dy (f(y)) • dy/dx

Complex numbers - If coefficients of polynomials are real then

Any complex roots will occur as a conjugate pair

Polynomial degree 2 will either have 2 real roots or 2 complex roots (a conjugate pair).

a polynomial of degree 3 (i.e. cubic) will either have 3 real roots or 1 real root and 2 complex roots (a conjugate pair).

If the coefficients are complex there are still n roots but they are not in any fixed pattern.

Any real n-degree polynomial, with n odd, must have at least one real root.

Trig identity to know

Cos^2x + sin^2x = 1

Cos^2x = 1/2 ( 1 + cos 2x)

Cos^2x = 1/2 ( 1 - cos2x)

Cos(2A) = cos^2A - sin^2A

Sin (2A) = 2sinAcosA

Polar form formula

Z = r(cosx + isinx)

First Order Differential Equation

dy/dx + P(x)y = Q(x)

∫ tanx dx

ln |secx| + C

∫cotx dx

ln|sinx| + C

∫-tanx dx

ln |cosx| + c

Integrating Factor

e^(∫P(x) dx)

General solution first order differential equations from equation given

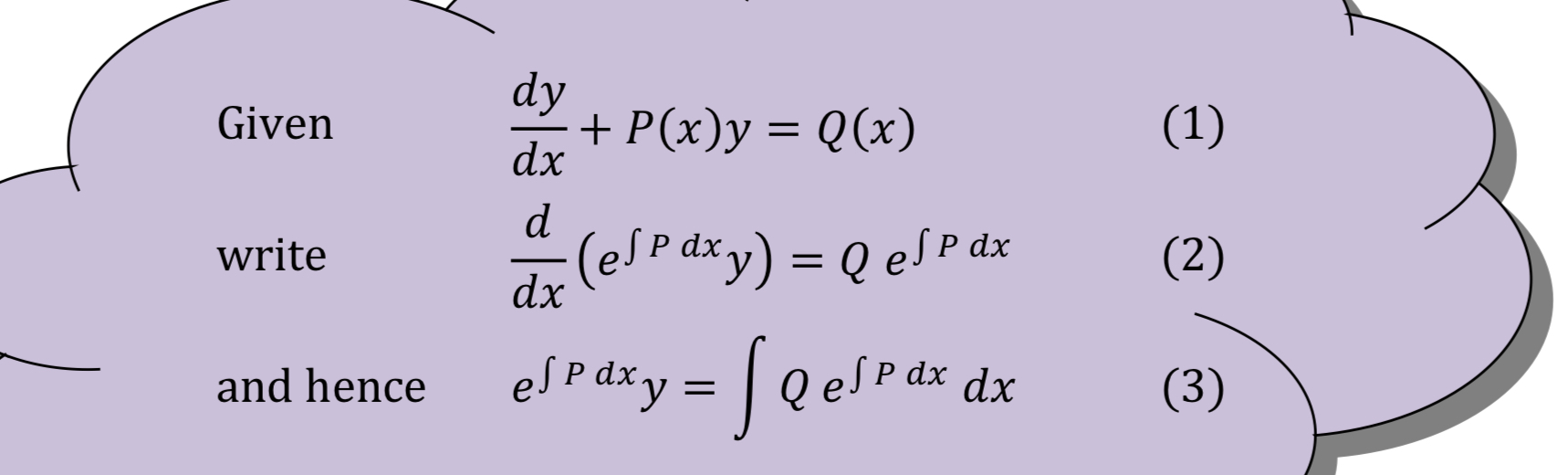
Form of first order differentiation

dy/dx + P(x)y = Q(x)

Homogenous equation general solution for real and distinct

Ae^ px + Be^qx

Homogenous equation general solution for real and equal

y = (Ax + B)e^px

Homogenous equation general solution for complex conjugates for p + iq

Y= e^px(Asinqx + Bcosqx)

General solution (GS) for non homogenous second order differential equation

GS = Complimentary function + Particular integral

Particular integral from f(x) = 2x + 1

y = px + q

Particular integral from f(x) = x^2 - 1

px^2 + qx + r

Particular integral from f(x) = 4e^2x

pe^2x

Particular integral from f(x) = 2sinx + cosx

psinx + qcosx

Particular integral from f(x) = 3sin2x

psin2x + qcos2x

General formula for first order differential equation

d/dx IFy = IFQ

What differentiates to ln(f(x)

f'(x) / f(x)

Reflection in the x-axis matrix

1 0
0 -1

Reflection in the y-axis matrix

-1 0
0 1

Enlargement by scale factor k

k 0
0 k

Reflection in the line y = x matrix

0 1
1 0

rotation 90° about the origin matrix

0 -1
1 0

General plane equation

a(x - x0) - b(y-y0) + c(z-z0)

Where (a,b,c) are components of normal vector n
And (x0, y0, z0) are the coordinates of a known point on the plane

Intersection of 2 or 3 planes method

Solve the plane equations simultaneously (e.g. Gaussian elimination)
• Three possibilities:

One solution → point of intersection

Only two unique equations → set z = t and solve in terms of t to give the equation of a line

• No solution → no point of intersection.
To find out why, check the normal vectors to see how many are parallel.

Line and plane intersection method

Write line in parametric form

Substitute for x, y and z into plane equation and solve to find lamda.

Substitute lamda into line equation to find point.

Distance formula

d = SQUARE ROOT OF ( (x2 - x1)^2 + (y2 - y1)^2 + (z2 - z1)^2 )

Vector equation different forms

Image

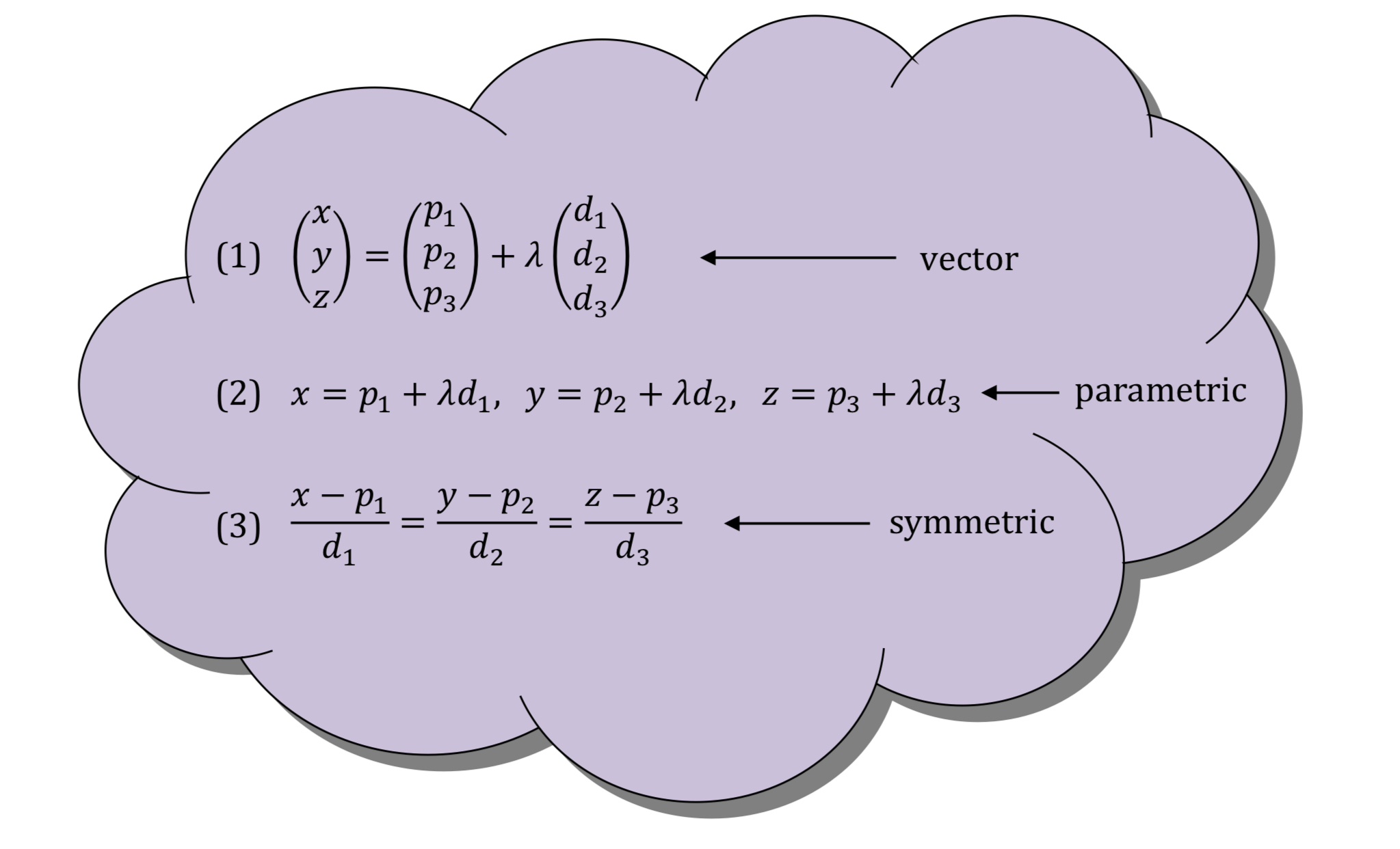
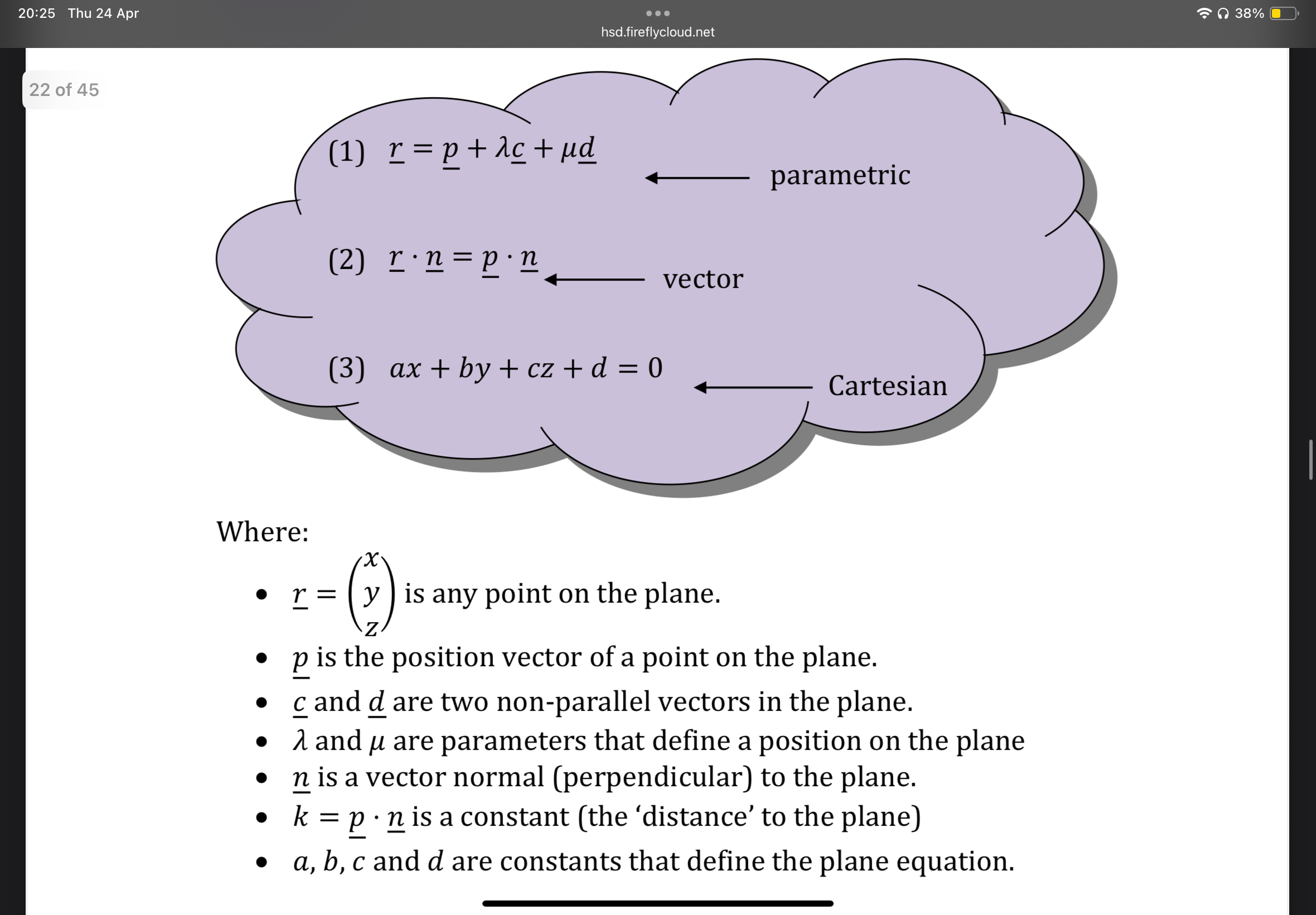
Plane equations different forms

Image

What does 1 equal in terms of trig identities

Cos²x + sin²x = 1

2cos²x - cos2x = 1

2sin²x - sin2x = 1

Double angle formula

sin(2x) = 2 sin(x) cos(x)

cos(2x) = cos²x - sin²x

Compound angles trigonometric identities

Sin(A ± B) = sinAcosB ± cosAsinB

Cos(A±B) = cosAcosB ± sinAsinB

Trig identities with sec, tan, cosec and cot

1 + tan²x = sec²x

cot²x + 1 = cosec²x

TanA (A±B)

(TanA ± TanB) / 1 ± tanA tanB

tan2A

2tanA / 1 - tan²A

Differentiate ln f(x)

f’(x) / f(x)

Tan x integral

ln (secx) + c

(Sigma with n on top and k=1 on bottom) of 1

n

Partial fractions of px + q / (x - a) (x - b)

A / (x - a) + B / (x-b)

Partial fractions of px + q / (x - a)²

A / (x - a) + B / (x - a)²

Partial fractions of px² + qx + r / (x-a) (x-b) (x-c)

A / (x - a) + B / (x - b) + C / (x - c)

Partial fractions for px² + qx + r / (x-a)² (x-b)

A / (x - a) + B / (x - a)² + C / (x - b)

Partial fractions for px² + qx + r / (x - a) (x² + bx + c)

A / (x - a)

+

Bx + C / (x² + bx + c)