CS115

Identifier

• Name of the function (name of constants)

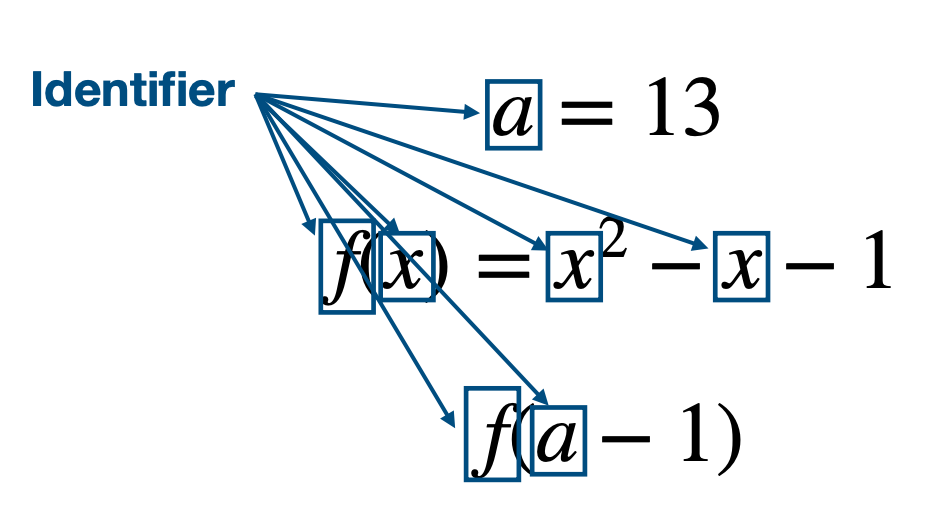
Parameter

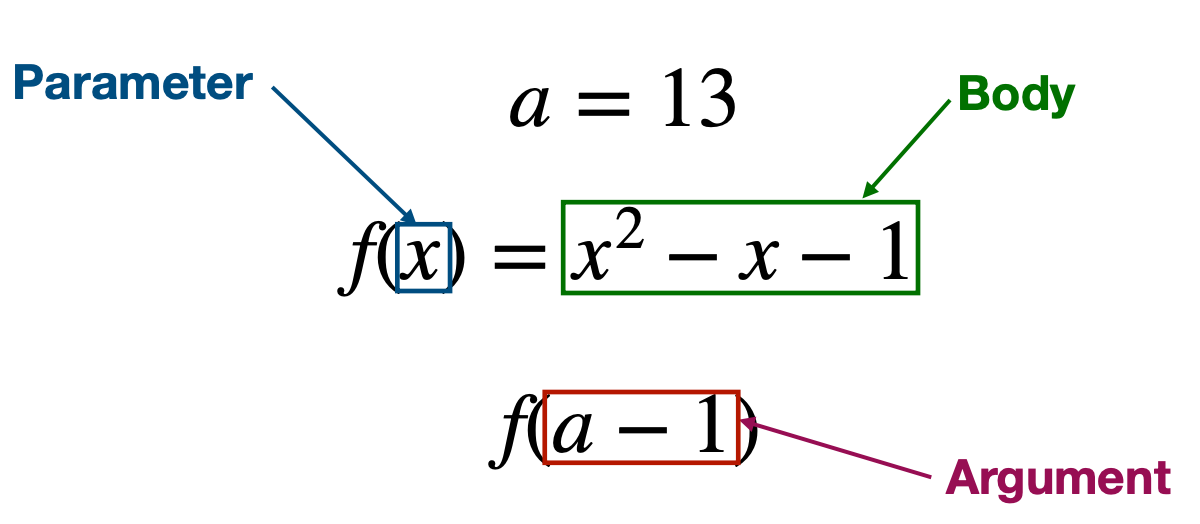
Argument

• Expression producing a value passed to the function

Constants

• Identifiers that are permanently bound to values

• Memorable name associated with a value

• Constants are replaced one at a time (small-sub rule) [define price1 1.75]

• (user-defined → big-sub → put all at once) [total-cost 4 6]

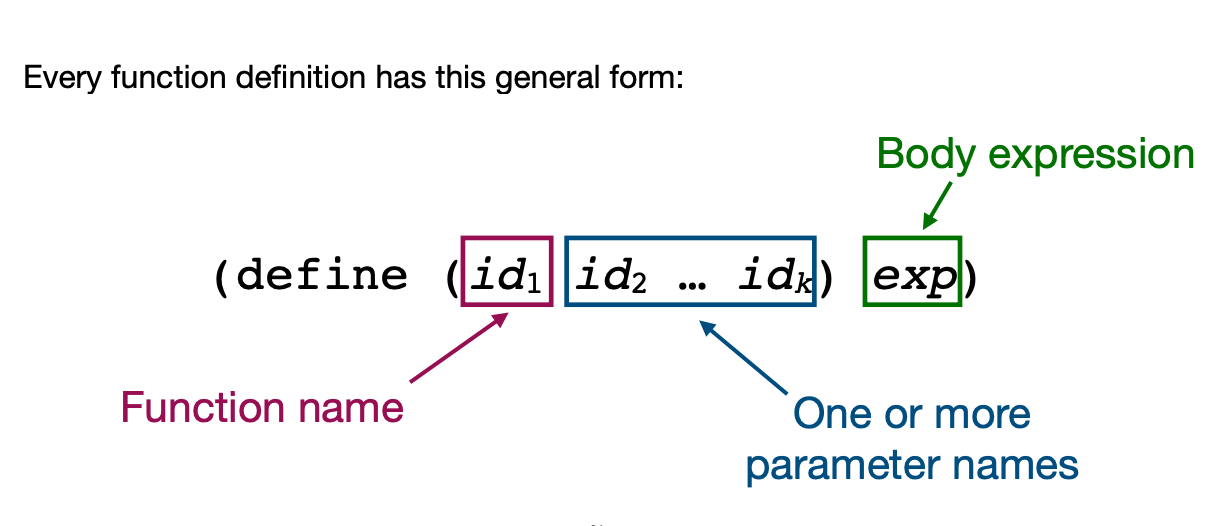
Function Definition Grammar

• Built-in

• User-defined

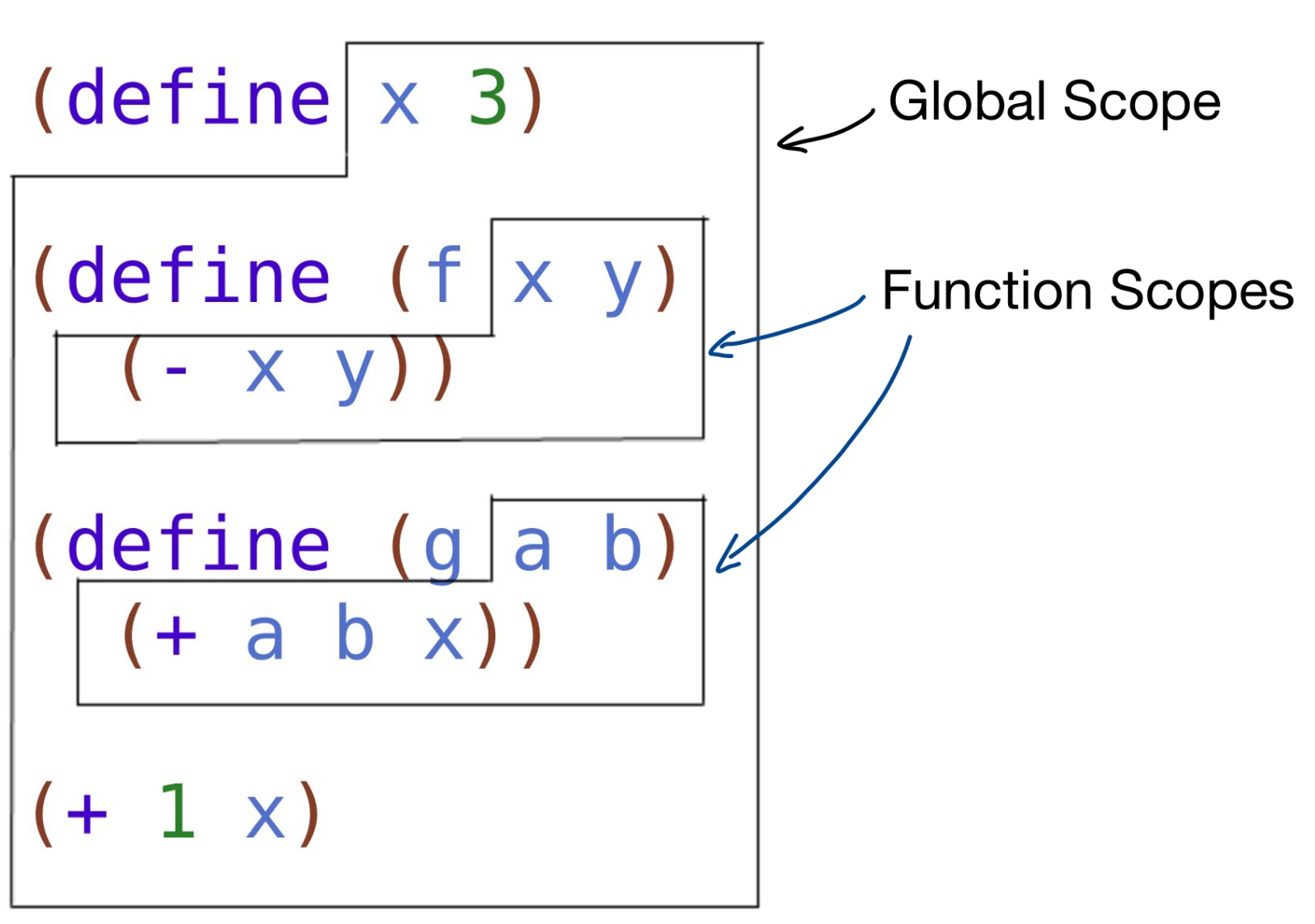
Scope

• Binding occurrence: Where the identifier comes into being

• Bound occurrences: Locations that refer back to a given binding occurrence

Scope: An identifier is the region of a program where the identifier binding occurrence is in effect

• Portion of the program code where a use of that name is tied back to the given definition

Global scope: Constants and functions introduced using define

Function scope: Parameter names and body of function definition

Semantic Model

• Method for determining the legal meaning of a program

Substitution

• Replace expression in a program with something slightly similar

• The program gets closer to being solved

Simplifying Built-In Functions

How do we simplify an expression like this one?

(+ 5 7 8)

• The + function is built in

• The best we can do with a built-in function is to write down the answer in one step: 20

• We call this the as-if-by-magic rule

Simplifying User-Defined Functions

With a user-defined function, we have a lot more information: the function body

(define (f x) (- (- (sqr x) x) 1))

(f 13)

• We replace the application by the body of the function, in which every occurrence of a parameter name is replaced by its corresponding argument value.

• This is the big-sub rule

Tracing

• Simplify it repeatedly until final value is obtained or encounter an error

Floating-Point

Inexact numbers (15-digits) (#i )

• Numbers with decimal (to show how precise they are)

Run-Time error

Evaluating an expression

25/0 cannot work

Define

• User-defined

• equivalent to the equal sign (=)

Helper function

Using an already defined function in place of another functions body

Ellipsis

(define (id₁ id₂ ... id_k) exp)

• Inner parentheses in the function definition contain a sequence of identifiers of unknown length (…)

Boolean

[=, <=, >]

• Consume numbers and produce booleans

Predicate

• Consume numbers and determine if it has a given property [even? odd? positive? negative?
  

• Type Predicate: Consumes value and if it belongs to a certain type [number? integer? boolean?]

• ALWAYS GIVE PREDICATES NAME ENDING IN ?

Boolean Algebra

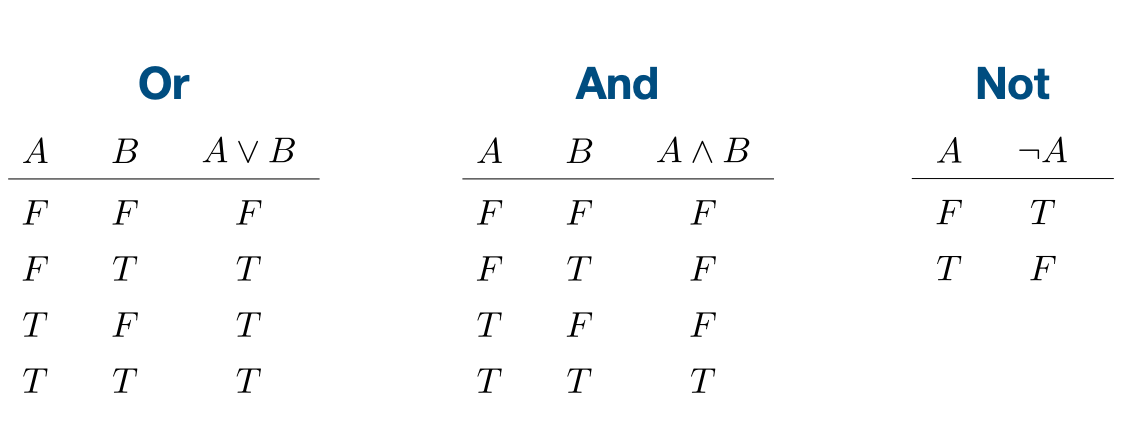
Boolean Operations

• (and exp1 … expk) produces true if all of the expi evaluate to true, and false otherwise

• (or exp1 … expk) produces true if any of the expi evaluates to true, and false otherwise

• (not exp) produces false if exp evaluates to true, and true if exp evaluates to false.

(see notes…)

Boolean Function Examples

Forbidden Boolean Operation

• Don’t put ‘=’ on booleans

• boolean=?

Semantics of Boolean Operations

• The not operation is just a regular built-in function: it consumes a Boolean value and produces its logical complement.

• But ‘and’ and ‘or’ have special powers: they stop processing as soon as the answer is certain:

20 (or (= x 0) (> (/ 1 x) 10))

(and (positive? x) (< (sqrt x) 5))

• This power is called short-circuiting. Because of short-circuiting, ‘and’ and ‘or’ or can't be functions—they need special-purpose substitution rules!

Substitution Rules for Boolean Operations

Conditional Evaluation

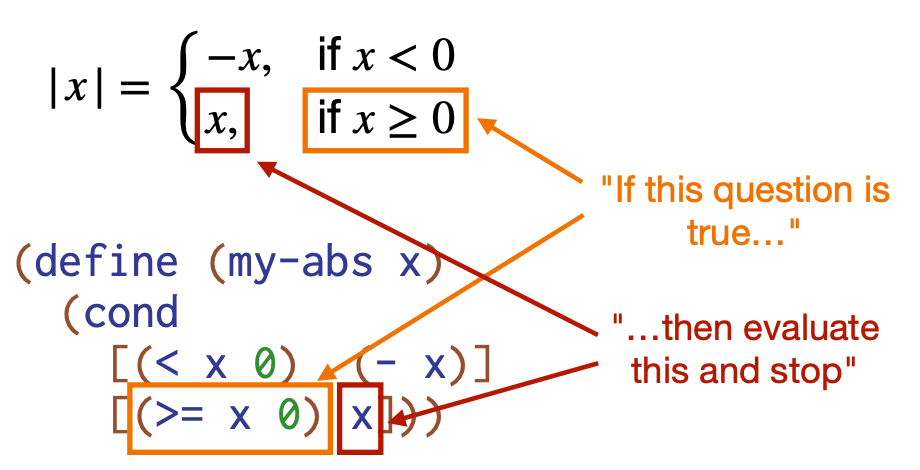
Grammar of cond

• Questions must evaluate to Booleans

• Evaluate questions in order; when a question evaluates to true, evaluate the corresponding answer and stop

• Final question can optionally be else, which always succeeds

Semantics of cond

• A cond expression can appear anywhere in a Racket program that any other expression is permitted.

• This feature of a programming language is called orthogonality

Simplifying Conditional Code

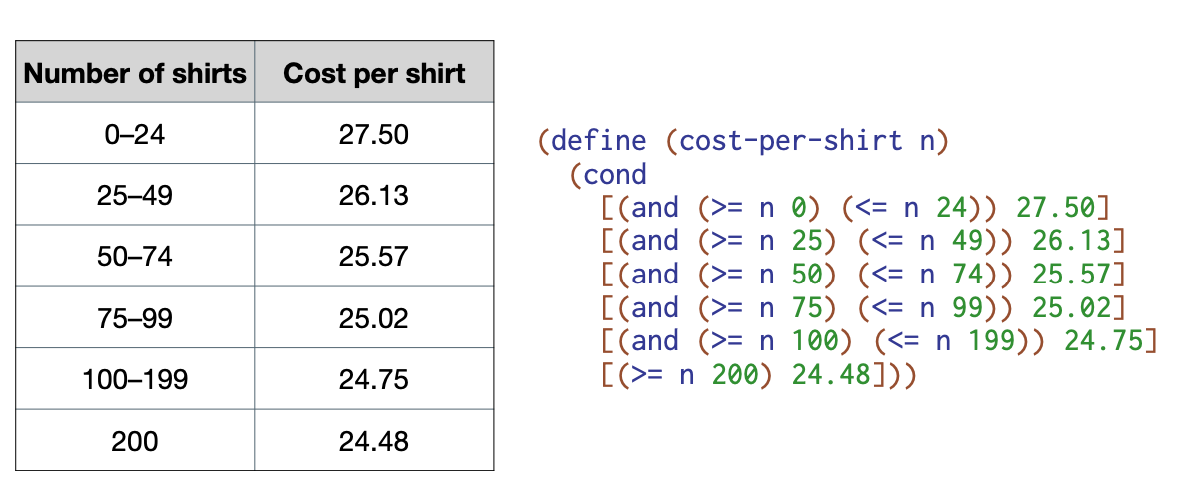
Short-circuiting

• Terminate a computation early if additional work won't change the result.

Orthogonality

• Aspect of the design of programming languages that helps keep them simple and understandable

String Functions

• A string is a block of text, i.e., a sequence of characters

• A string literal can be written by enclosing text in double quotes

string?: type predicate for strings

string=?: consumes two strings, produces a boolean indicating whether they have the same characters

string-length: consumes a single string, produces the number of characters in the string

string-append: consumes any number of strings, and produces a single new string in which all the characters of the consumed strings are glued together

string Indices: Assign consecutive indices to the characters in a string, starting from zero: [0 1]

Escaped Characters

• Some special characters must be preceded by a backslash character (\) so that they don't confuse Racket

• Inside a string, write \" for a double quote and \\ for a backslash. Each is still a single character

Substrings

• (substring s a b): produce a new string consisting of the characters of string s from index a up to, but not including, index b

• We require 0 ≤ a ≤ b ≤ (string-length s) 11

• (substring s a): a convenient shorthand for (substring s a (string-length s)), i.e., the substring from index a to the end of the string

Symbols

• A symbol is an identifier preceded by a single quotation mark; label information, define sets of categories

• symbol?: type predicate for symbols

• symbol=?: consumes two symbols, produces a boolean indicating whether they're the same

• Symbols are multiple choice, strings are short answer

• Symbols are atomic, strings are compounds

Symbol Example: Numbers with Infinity

Generalized Equality

• The built-in function equal? consumes two values of any types and checks if they're equal

Comments

(;) Ignore current line

(;;) Ignore full-line comment

Purpose

• Multi-line comment

• Starts with the function name

• “produces..”

• Explains what the function does (NOT HOW IT DOES IT)

• Mentions all parameter names

Contract

• Comments that describe the domain and range of the function

• Domain and range are sets

Examples:
;; sum-of-squares: Num Num -> Num
;; string-length: Str -> Nat
;; symbol=?: Sym Sym -> Bool

When needed, we add an optional requires clause under the contract, where we put any additional constraints on domain types:

;; Requires: 2 <= x < 19
;; Requires: s is not the empty string
;; Requires: a >= b

Examples

• Show reader what your code might look like

• Force you to think the problem through by solving cases by hand

• Shows the function produces the right answer

Header + Definition

• Define the portion of the function

• Add extra ellipsis (…)

(define (sum-of-squares p1 p2)
...)

Tests

• Additional check-expect to verify the function produces the right answers

;; Tests:

(check-expect (sum-of-squares -1 -2) 5)
(check-expect (sum-of-squares 0 2.5) 6.25)
(check-expect (sum-of-squares -10 2.5) 106.25)

Check-expect

(check-expect test-expression expected-result)

• Consumes 2 expressions and evaluates it

Black-Box Testing

• Tests that don’t depend on how the function works (incorrect answers)

White-Box Testing

• Derived from the function definition (correct answers)

Fine-Grained Coverage

• Must check all ways of testing

(define (charming? x)
(and (>= x 5) (<= x 17) (not (= x 13))))

Testing Breakpoints

Breakpoint: Where the function changes

Testing Inexact Numbers

• We never check inexact numbers for equality:
  > (equal? (sqr (sqrt 5)) 5)

  false

• By extension, we're not allowed to use check-expect with inexact numbers
• check-within: includes a third argument: a numeric tolerance

> (check-within (sqr (sqrt 5)) 5 0.0001)
The test passed!

Final Design Recipe With HELPER FUNCTION

List length

• Have a lost with (n) things in it

• Add one more to obtain a new list (n+1)

1. A way to describe a list with nothing in it (empty)

2. Way to add one new thing into the existing list

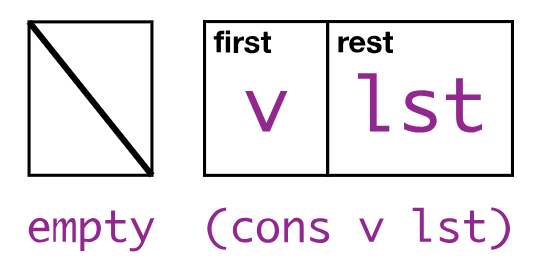
The empty list

• Nothing in it

• Use it as a starting point

> empty

• Kinda like ‘true’: a special defined value that means only itself

> (empty? empty)
true

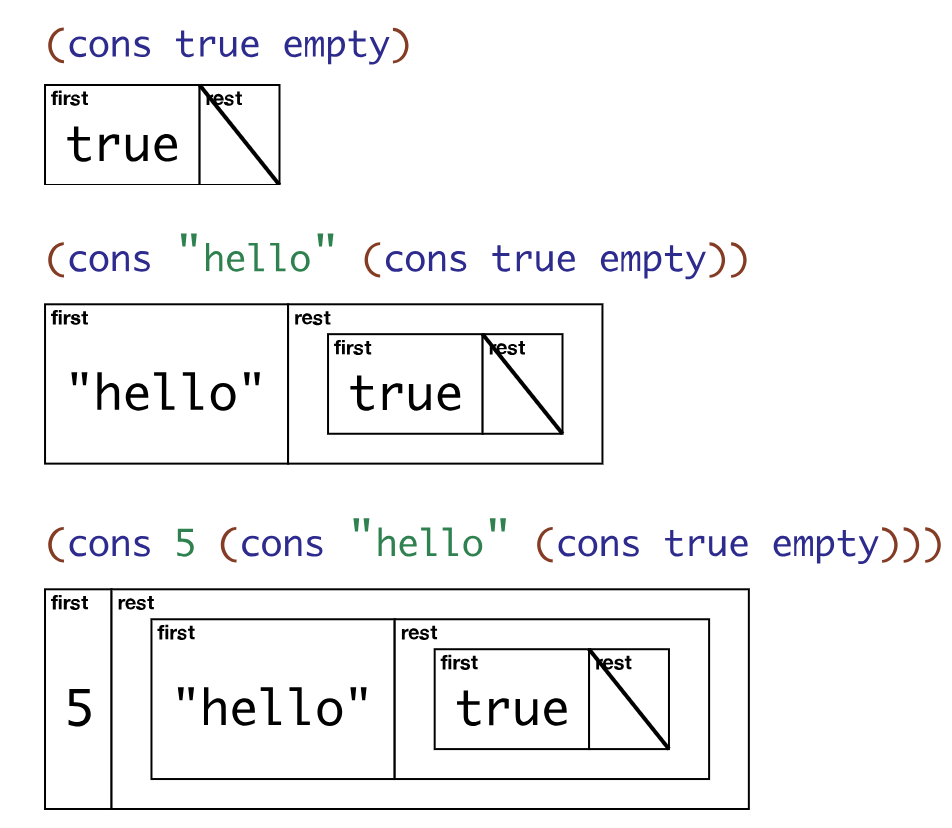
“Consing” a list

1. The empty list is a list

2. Given an existing list, you can build a new list that has one more item added at the beginning

cons “construct” = produces a new list

• Consume two arguments

  1. Any type at all

  2. Must be a list

Cons Cell

• cons function produces a special value of a new type

• Verify by its predicate, cons?

> (cons? empty) ;; the empty list isn't a cons
false

List

> (list? empty)
true

> (list? lst2)
true

> (list? "I'm a list")
false

First & Rest

• (first (cons v lst)) ⇒ v

• (rest (cons v lst)) ⇒ lst

> (first suits)
'spades

> (rest suits)
(cons 'hearts (cons 'diamonds (cons 'clubs empty)))

CANNOT USE FIRST OR REST ON AN EMPTY

> (first empty)
first: expects a non-empty list; given: empty

> (rest empty)
rest: expects a non-empty list; given: empty

Visualization using nested boxes

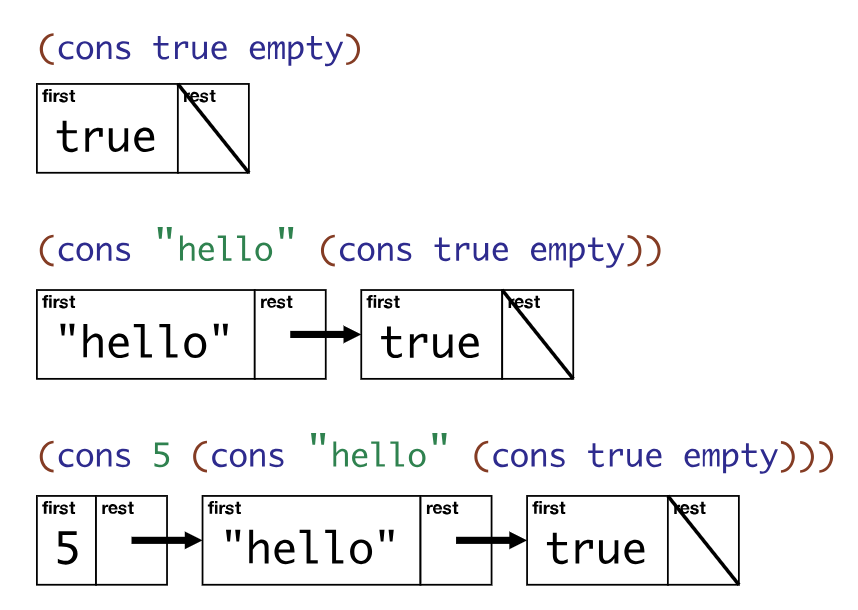
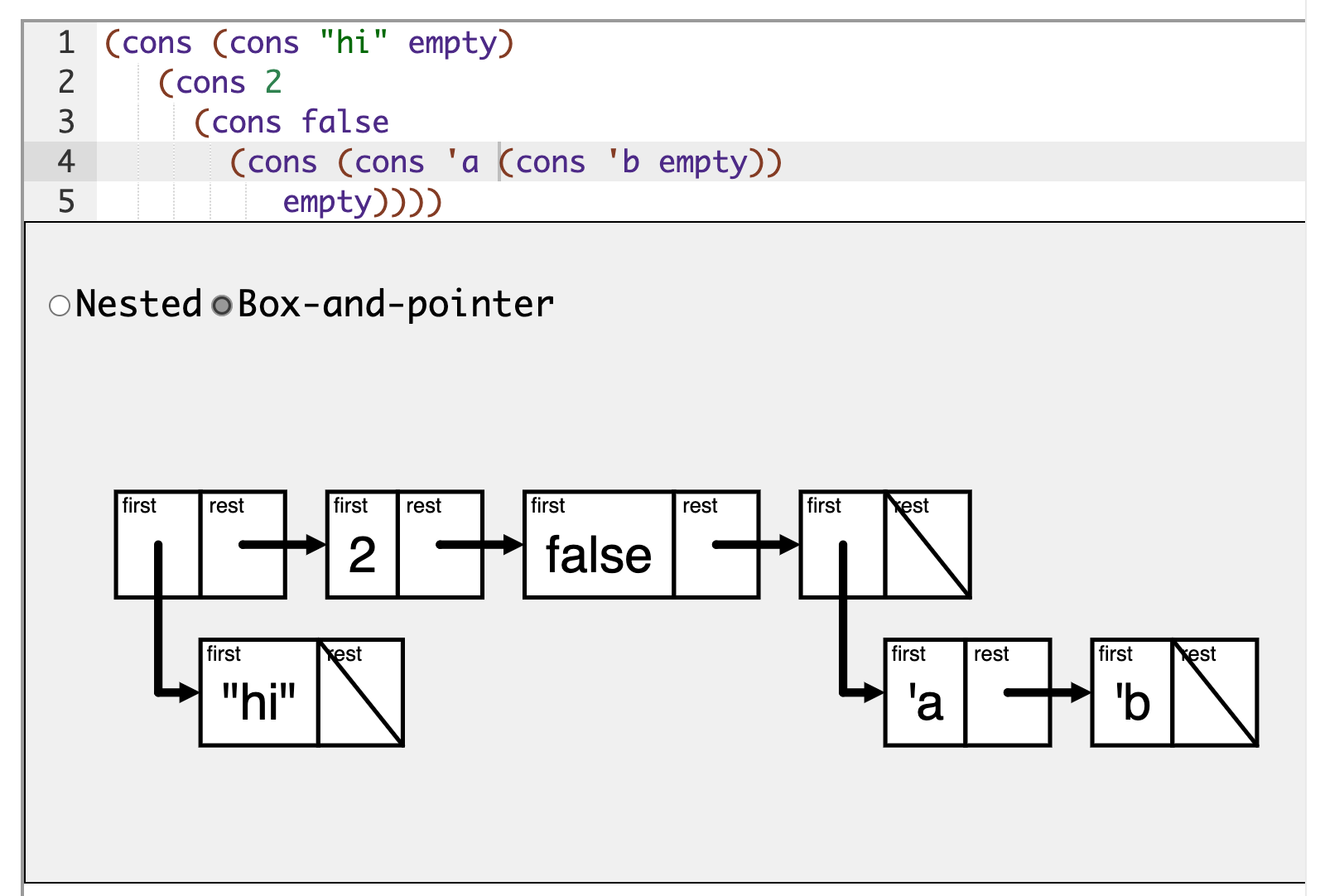
Visualization using boxes and arrows

• box-and-pointer visualization

sum-list

• consumes a list of numbers (lon) and produces the sum

Data-Defintion

• A type is a group of values

• Create new types if Racket doesn’t have the one you need

• Name the new type and use it like any standard type

• A data definition introduces a new type, here called ExtNum

• ExtNum can be either a Num or a Sym

• This type is like a union of Num and Sym (i.e., it can be one or the other)

• We use a bulleted list to show its possible values

More Data-Definition

Folding Idioms

‘folding’ the contents of the list into a single value

Mapping Idiom

Produces a new list of the same length (can also negate)

Filtering Idioms

Creating a new list with given requirements (sublist)

Auxiliary Parameters

string literal

(i.e., a string value in its final form)

Wrapper Function

A simple, non-recursive function that initiates a large computation, often preparing data for recursive processing and polishing up the result

Homogeneous list

A list whose elements are all of a given type