General Physics 203 - Lecture 5, Circular Motion/Centripetal Force Ch.3.7-3.8, 6.1-6.6

Circular Motion

constant speed, but different velocity, since the direction of their velocity changes.

Uniform circular motion

the motion of an object traveling at a constant (uniform) speed on a circular path.

same speed (constant); same magnitude of the vectors

In circular motion, that object’s velocity is changing

so the object is accelerating, even if its speed is constant.

Change in direction for velocity vector; change in velocity over time

Acceleration

Period T

one revolution in seconds

Speed and Period T are related

v = 2(pi)r/T

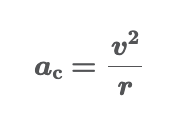
centripetal acceleration

velocity vector always points toward the center of the circle for circular motions and continually changes direction as the object moves.

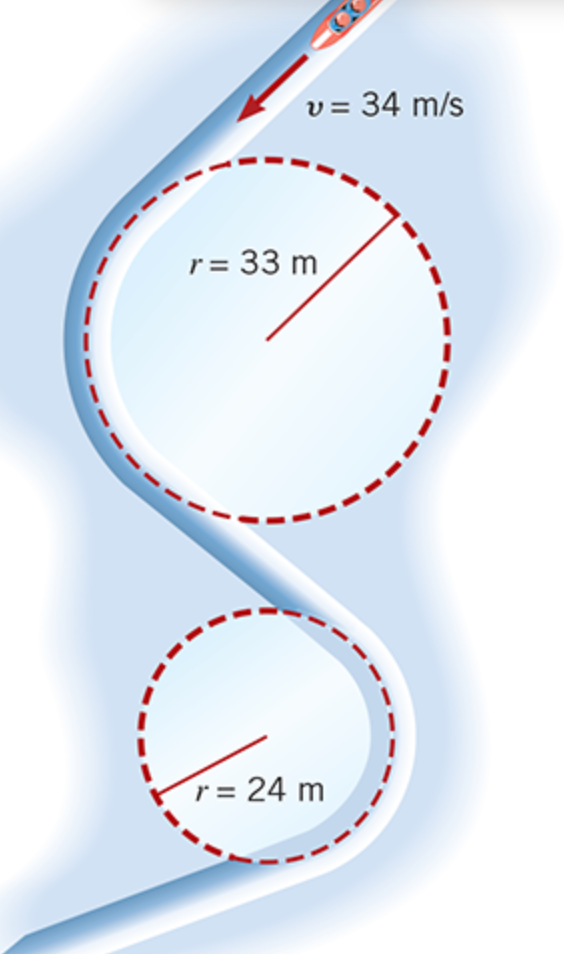
his bobsled travels at the same speed around two curves with different radii. For the turn with the larger radius

the sled has a smaller centripetal acceleration.

going around tight turns (smaller r) and gentle turns (larger r) at the same speed entails different centripetal accelerations.

inverse relationship with size of turns and the force of centripetal acceleration

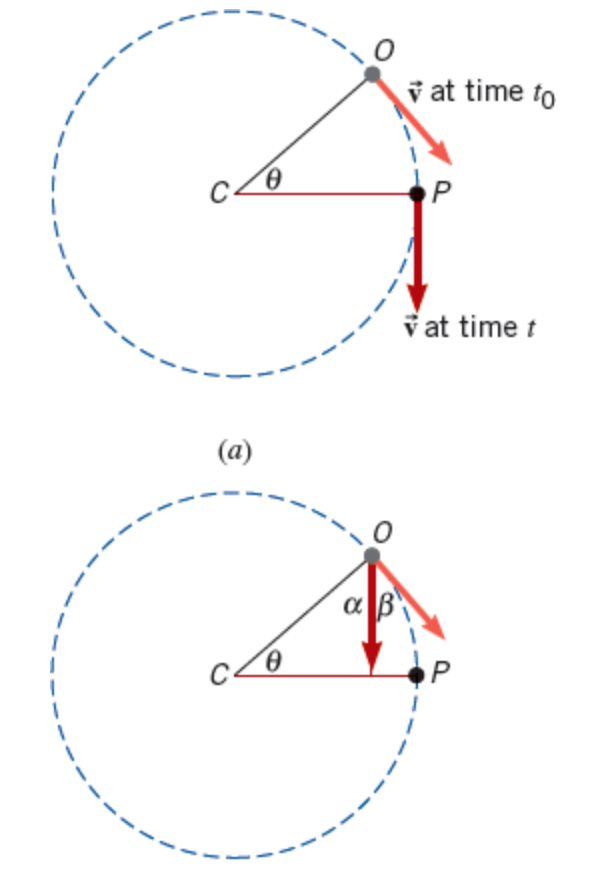
As the object moves from O to P

the radius traces out the angle θ, and the velocity vector changes direction

Velocity vectors are tangent to this

each point on the circular motion

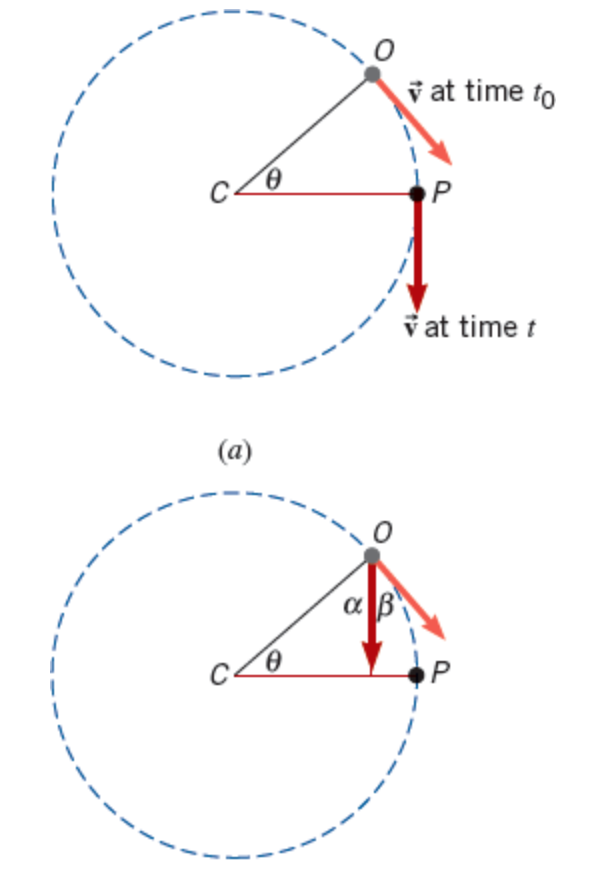
To emphasize the change, part b of the picture shows the velocity vector removed from point P, shifted parallel to itself, and redrawn with its tail at point O.

The angle β between the two vectors indicates the change in direction

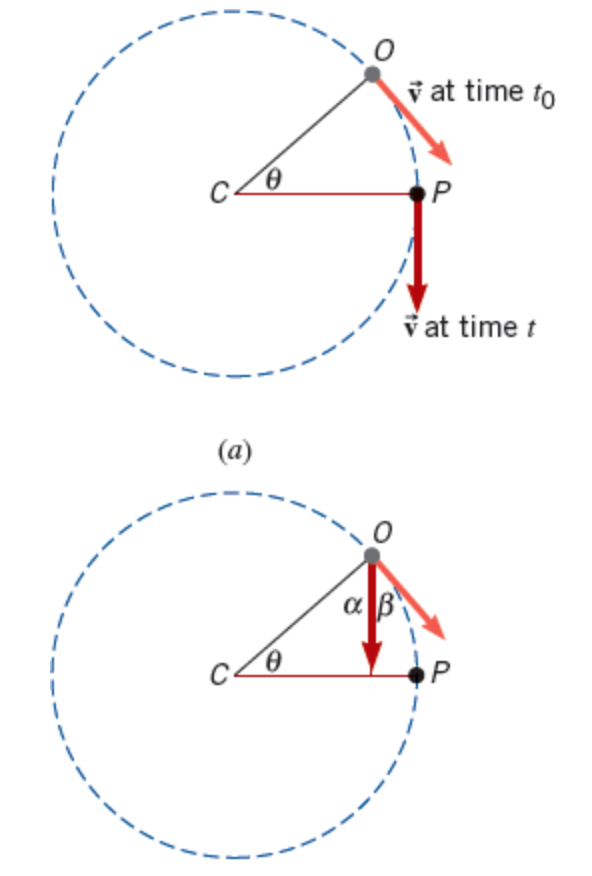
Since the radii CO and CP are perpendicular to the tangents at points O and P

α + β = 90° and α + θ = 90°. Therefore, angle β and angle θ are equal.

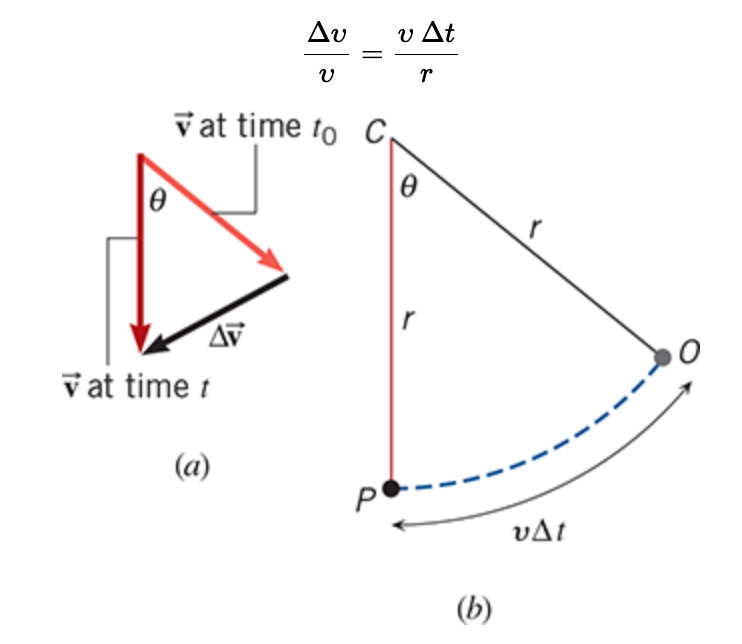
The radii of triangle 1 are similar triangles to this

the velocity vectors making a velocity triangle

An object is in equilibrium when it has zero

acceleration (no change in direction at the same speed)

Newton’s second law indicates that whenever an object accelerates, there must be a

net force to create the acceleration

Thus, in uniform circular motion there must be a net force to produce the

centripetal acceleration.

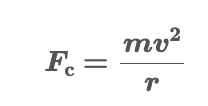
The net force causing the centripetal acceleration is called the

centripetal force Fc, and points in the same direction as the acceleration—that is, toward the center of the circle, and continually changes direction as the object moves

Centripetal force is the net force causing acceleration

Fc is the vector sum of all the force components that point along the radial direction

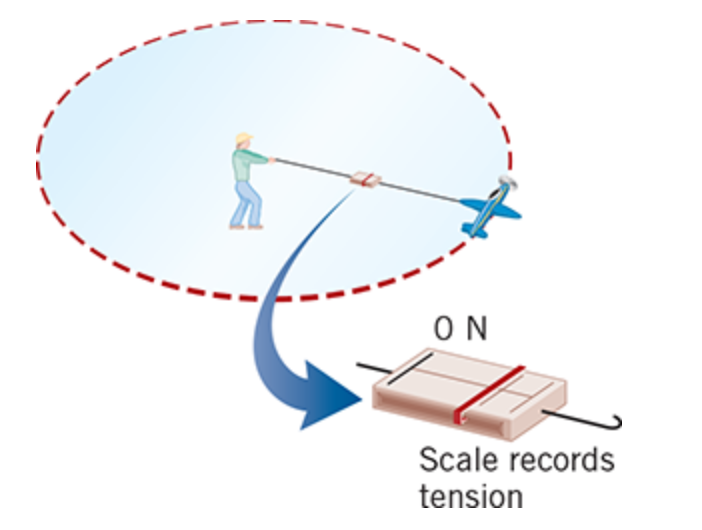
Since the plane flies on a circular path, it experiences a

centripetal acceleration that is directed toward the center of the circle.

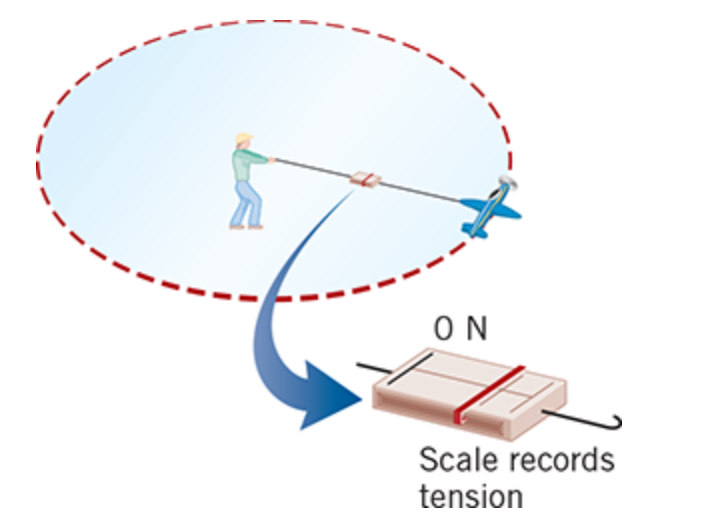
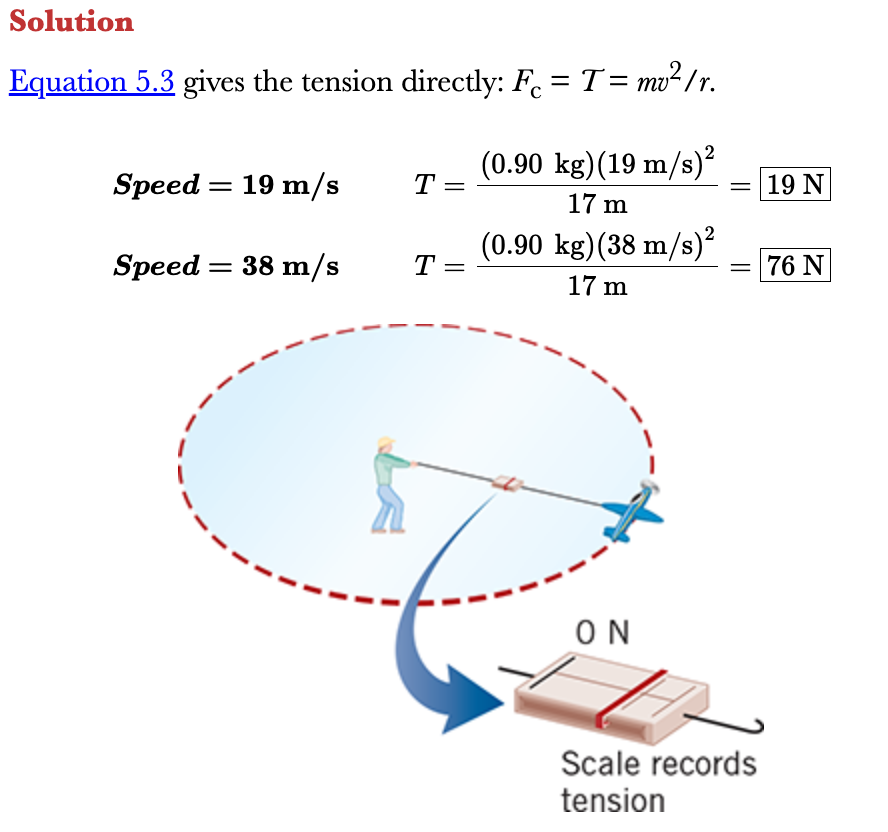
According to Newton’s second law of motion, this acceleration is produced by a net force that acts on the plane,

and this net force is called the centripetal force. The centripetal force is also directed toward the center of the circle

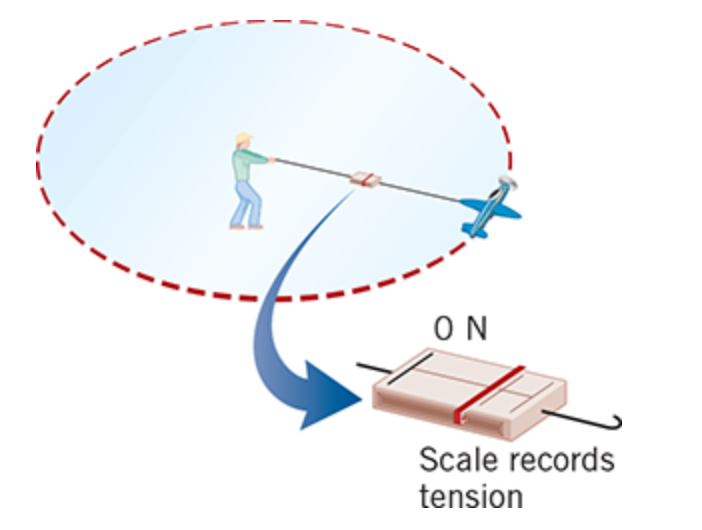
Since the tension in the guideline is the only force pulling the plane inward, it must be

the centripetal force.

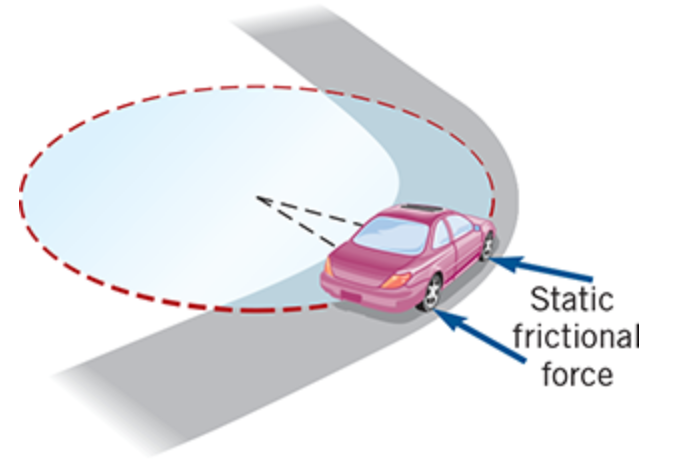
Without a line holding the car in lane of its circular motion, the Fc holding a car in place is

static frictional force

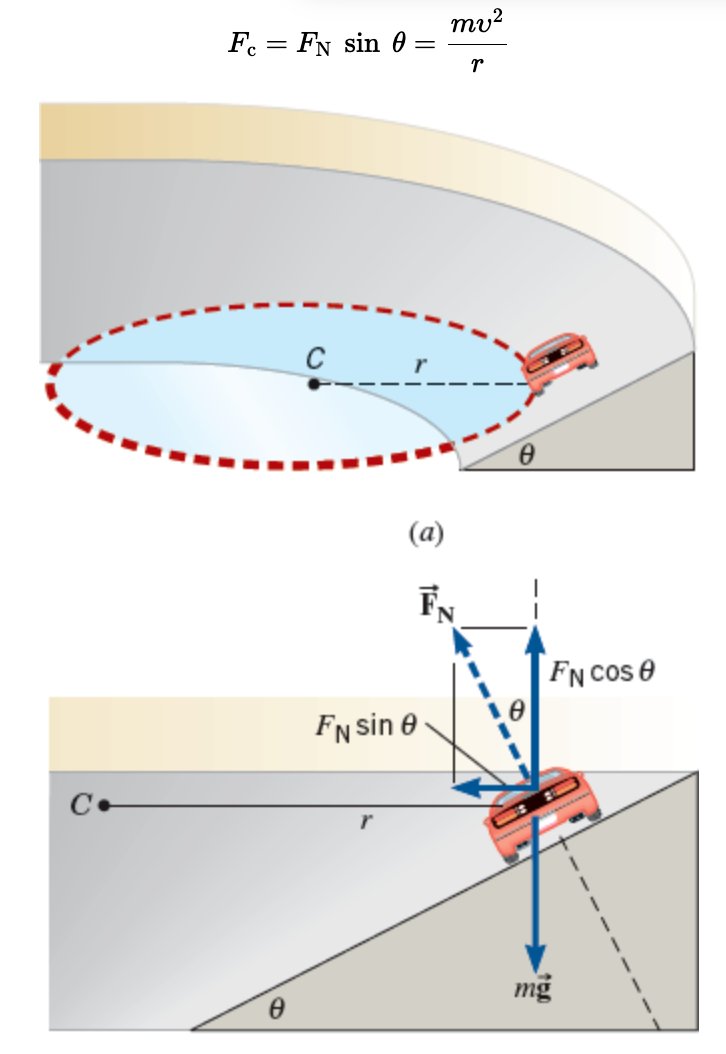
Centripetal Force when the object is on an angle

The banking angle is θ, and the center of the circle is at C. (b) The forces acting on the car are its weight m𝑔→ and the normal force 𝐹_N.

A component FN sin θ of the normal force provides the centripetal force.

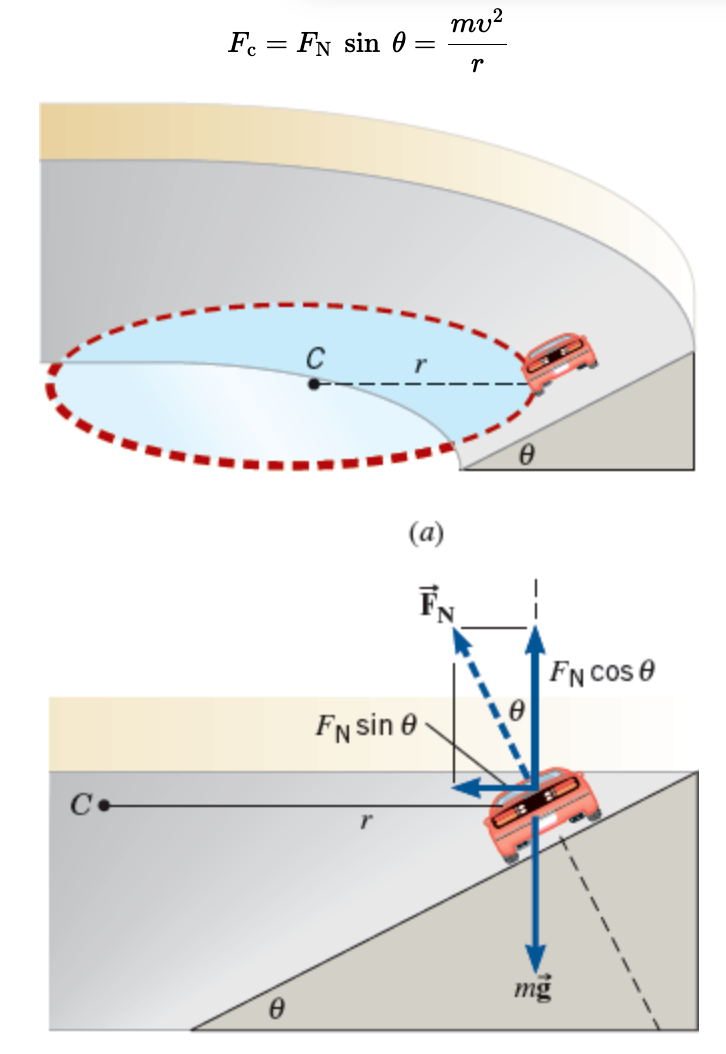
The vertical component of the normal force is FN cos θ and, since the car does not accelerate in the vertical direction,

this component must balance the weight mg of the car.

Therefore, FN cos θ = mg

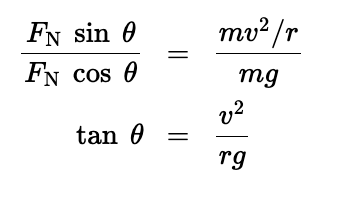
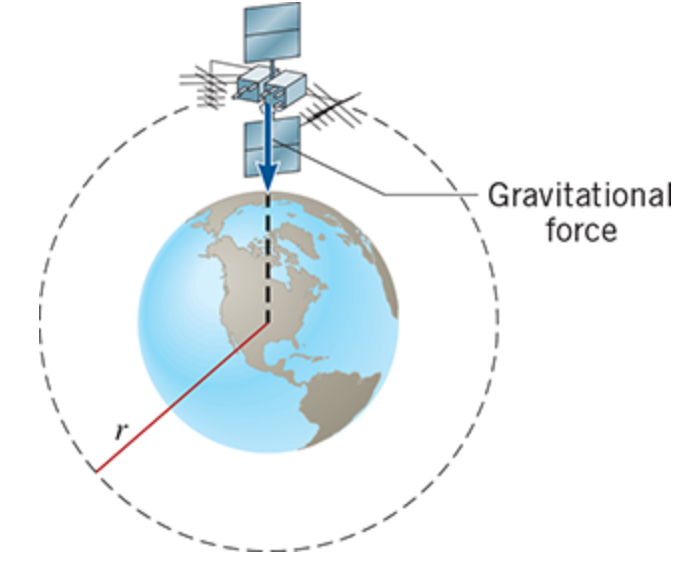
Satellites that orbit around Earth is kept on its circular path by a centripetal force. The Fc is this

The gravitational pull of the earth provides the centripetal force and acts like an invisible guideline for the satellite.

Since the gravitational force is the only force acting on the satellite in the radial direction, it alone

provides the centripetal force

If the satellite is to remain in an orbit of radius r, the speed must have

precisely this value

the closer the satellite is to the earth, the smaller is the value for r and the

greater the orbital speed must be.

Consequently, for a given orbit, a satellite with a large mass has

exactly the same orbital speed as a satellite with a small mass.

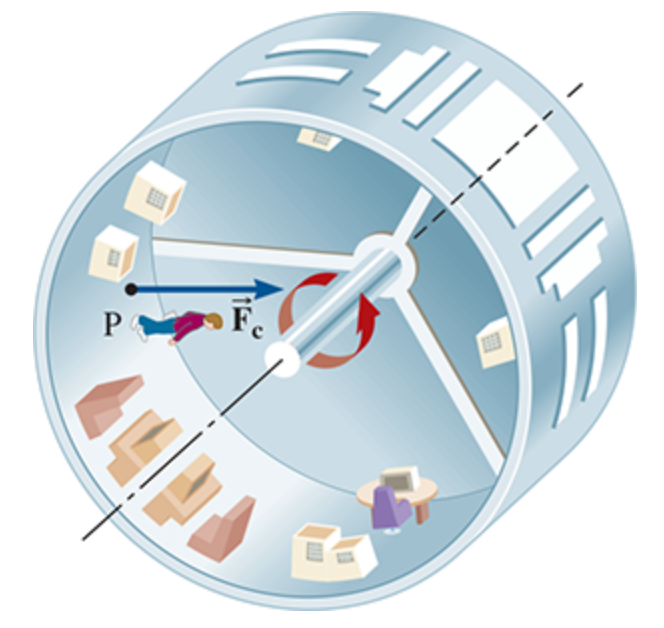
The surface of the rotating space station pushes on an object with which it is in contact and thereby provides the

centripetal force that keeps the object moving on a circular path

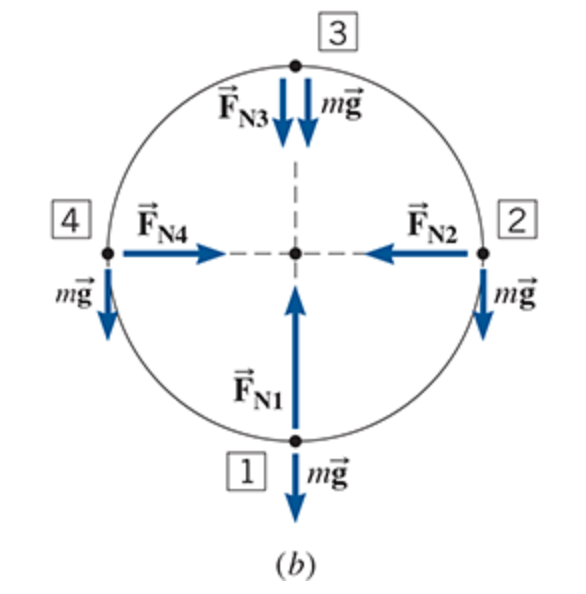
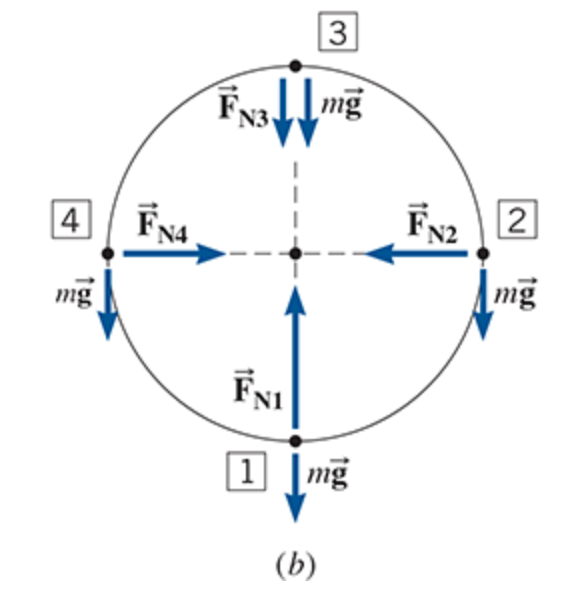
F_N is drawn perpendicular to the direction of the object moving. mg always points down

more than one force contributes to this net force (mg and F_N)

Vectors pointing opposite directions are subtracted while

vectors pointing in the same direction are added together.

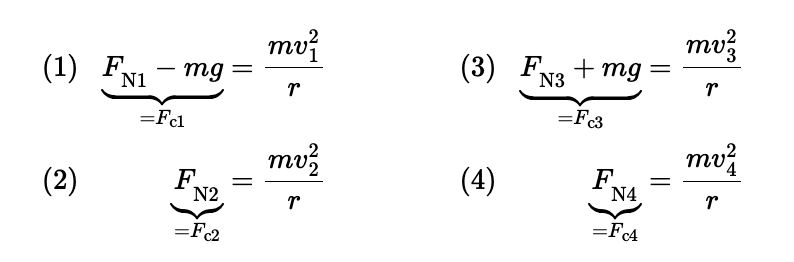
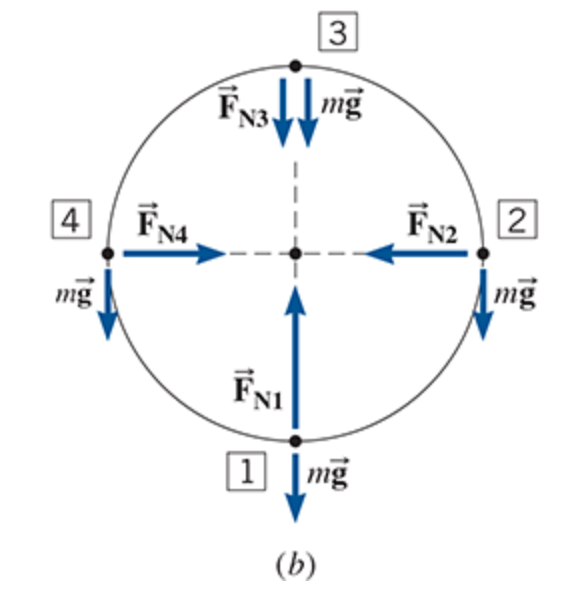
As the cycle goes around, the magnitude of the normal force changes. It changes because the speed changes and because the weight does not have the same effect at every point

At the bottom, the normal force and the weight oppose one another, giving a centripetal force of magnitude FN1 − mg. At the top, the normal force and the weight reinforce each other to provide a centripetal force whose magnitude is FN3 + mg.

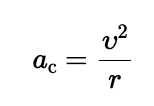
An object in uniform circular motion experiences an acceleration, known as

centripetal acceleration.

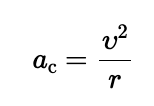
The direction of the centripetal acceleration vector always points toward the

center of the circle and continually changes as the object moves.

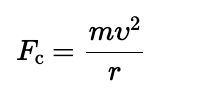
To produce a centripetal acceleration, a net force

pointing toward the center of the circle is required. This net force is called the centripetal force

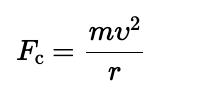
The direction of the centripetal force vector, like that of the centripetal acceleration vector, always points

toward the center of the circle.

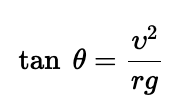
Banked Curves: A vehicle can negotiate a circular turn without relying on static friction to provide the

centripetal force, provided the turn is banked at an angle relative to the horizontal.

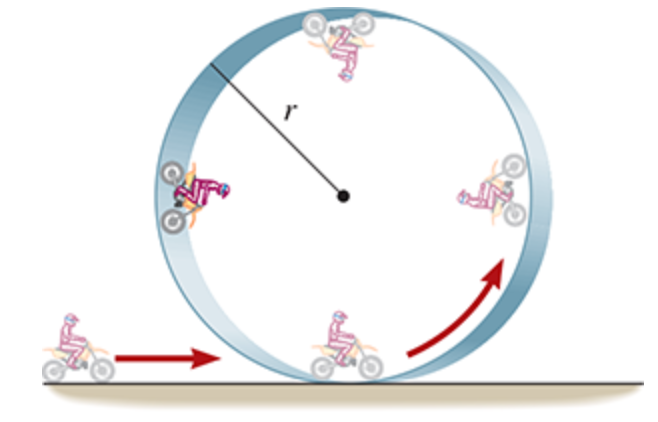
Vertical circular motion occurs when an object, such as a motorcycle, moves on a vertical circular path. The speed of the object often

varies from moment to moment, and so do the magnitudes of the centripetal acceleration and centripetal force.