5.3 oscillations

displacement

x, the distance from the equilibrium position

amplitude

A, the maximum displacement

period

T, the time taken to complete one full oscillation

frequency

f, the number of oscillations per unit time

phase difference

ϕ, the fraction of an oscillation between the position of two oscillating objects
given by Δt/T x 2π

angular frequency

ω, the rate of change of angular position
given by 2πf

simple harmonic motion

a type of oscillation where the acceleration of the oscillator is directly proportional to the displacement from the equilibrium position, and acts towards the equilibrium position
a = -ω²x
where a is the acceleration, ω is the angular frequency and x is the displacement of the oscillator
the negative sign si there as the direction of acceleration is always towards equilibrium so against displacement

isochronois oscillation

where the period of the oscillation is independent of the amplitude, i.e. in simple harmonic motion

investigating the period and frequency of SHM

an oscillator is set, and the time period for 10 oscillations (or another reasonable number) is measured, the equilibrium position may be marked for accuracy with a fiducial marker
the frequency is equal to the reciprocal of the period (for 1 oscillation)

displacement of a simple harmonic oscillator

x = Asinωt if the oscillator begins at the equilibrium position
x =
Acosωt if the oscillator begins at the amplitude position
where x is the displacement, A is the amplitude and ω is the angular frequency

velocity of SHM

v = ±ω√(A² - x²)
where v is the velocity, ω is the angular frequency, A is the amplitude and x is the displacement
maximum velocity (attained at the equilibrium position) is given by ωA

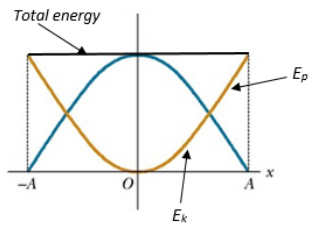
kinetic and potential energy in SHM

energy is exchanged between these forms, where the maximum KE (and no PE) occurs at the equilibrium point and the maximum PE (and no KE) occurs at the amplitude positions
total energy is conserved when damping is ignored

damping

the process by which an oscillation loses energy to resistive forces such as drag and friction, decreasing the oscillations of the amplitude over time

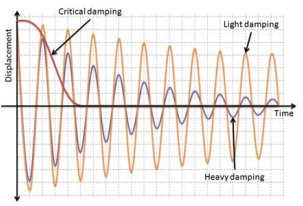
damping types

-light damping: amplitude decreases exponentially (e.x. pendulum oscillating in air)
-heavy damping: amplitude decreases dramatically (e.x. pendulum oscillating in water)
-critical damping: object stops before one oscillation is completed (e.x. pendulum oscillating in viscous liquid)

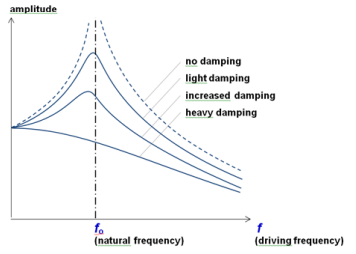
natural frequency

the frequency an object would oscillate at indefinitely if external forces were removed

free oscillation

when an object oscillates free of external forces, this is free oscillation, and it will oscillate at its natural frequency

forced oscillation

when a periodic driving force is applied to an object, causing it to oscillate at a particular frequency

resonance

when the driving frequency applied to an oscillating object is equal to its natural frequency the amplitude of oscillation rapidly increases, this is called resonance
if there is no damping it will continue to increase until the system fails, more damping lowers the amplitude and the frequency corresponding to the maximum amplitude

examples of forced oscillations

-pushing a child on a swing
-playing musical instruments
-changing radio stations (you match your RF to the f of the broadcase)
all of these can become examples of resonance if the resonant frequency is met