(DISC STR 1) Preliminary

Proposition

It is defined as a statement to be proved, explained, or discussed.

Statement

It is a declarative sentence that is either false or true (not both).

Capital letters

When represented in tables, these are usually used for proposition.

T

In letter symbols, we use this to represent a true statement.

F

In letter symbols, we use this to represent a false statement.

1 = true

0 = false

Using numerical symbols, what represents true and false?

Laws of thought

This is the basis of all logic for scholars who saw themselves as carrying on the Aristotelian and Medieval tradition in logic.

• Law of Identity or “Logical Identity”

• Law of Excluded Middle

• Law of Non-Contradiction

These are the bases for propositional logic or based on scholars are the “laws of thought.”

Law of Identity or “Logical Identity”

It is the notion that things must be, of course, identical with themselves.

Law of Identity or “Logical Identity”

Example: “If water is water, then by the law of identity, anything we discover to be water must possess the properties.”

Law of Excluded Middle

It is the idea that every proposition must be either true or false, not both and not neither.

Law of Excluded Middle

Example: “If the date today is January 1, the proposition P is true only; it cannot also be false.”

Law of Non-Contradiction

Logically correct propositions cannot affirm and deny the same thing.

Law of Non-Contradiction

Example: “Is it January 1 today? The answer could only be yes or no and not both.”

Truth Table

It is a chart to keep track of all the possibilities in the proposition.

Compound Proposition

It is a proposition constructed by combining one or more existing propositions.

• Negation

• Conjunction

• Disjunction

• Implication

• Biconditional

• XOR

These are types of logical connectives.

Negation

It combines propositions using the keyword not.

Negation

It states the opposite of the proposition.

Negation

We use the symbol ( ~ ) or ( ¬ ) attached to the representation of the proposition.

Conjunction

It combines propositions using the keyword and.

Conjunction

It would only be true if both initial propositions are true.

Conjunction

The symbol (^) is used to represent this logical connective.

Disjunction

It combines proposition using the keyword or.

Disjunction

It will be true if one of the propositions is true.

Disjunction

The symbol (v) is used to represent this logical connective.

Implication

The combined propositions are formed as if-then statements.

Implication

Thy symbol used to represent this logical connective is an arrow (→).

Antecedent

In Implication: the first proposition is called?

Consequence

In Implication: the second proposition is called?

1. Converse

2. Contrapositive

3. Inverse

These are other implications that can be formed from A → B

Converse

It is the reverse of the implication which means that the second statement is now the antecedent.

B → A

Contrapositive

The propositions are interchanged (become Converse) and negated.

~B → ~A

Inverse

The original propositions are negated.

~A → ~B

Biconditional

A statement combining a conditional statement with its converse.

Biconditional

The words if and only if is used in this proposition.

Biconditional

The symbol used for this logical connective is (→) [arrow na back-to-back].

Biconditional

Both propositions should have the same value.

XOR

Read as exclusive or and is a version of a disjunction that does not allow both propositions to be true simultaneously.

XOR

The symbol used for this logical connective is (⊕) .

XOR

It is often used for bitwise operations, particularly in computer science.

Tautology

It is any statement that is TRUE regardless of the truth values of the constituent parts

Contradiction

It is any statement that is always FALSE regardless of the truth values of the parts.

Contradiction

It is the opposite of a tautology.

Contingency

It is any statement that is neither a tautology or a contradiction.

Logically Equivalent

When two different compound propositions have exactly the same truth value in every case, then the propositions are?

Logical Equivalence

The symbol used to denote this is ≡

Set

It is a well-defined and an unordered collection/aggregate of objects of any kind.

Objects

They are referred to as elements or members of the set.

Roster Method

It is also known as Listing Method.

Roster Method

Example: S = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

Descriptive Method

It is also known as Set Builder Method.

Descriptive Method

Example: S = {whole numbers less than 10}

Universal Set

It is the set that contains all elements relevant to a particular discussion or problem.

Finite Set

The number of elements in a set is countable.

Infinite Set

The number of elements in a set is not countable.

Set Equality

It states that the two given sets are identical, if and only if they contain exactly the same elements.

Subset

It is a set contained in a larger set or in an equal set.

Subset

This symbol ⊆ means:

Universal set of all numbers

The symbol U means:

For every

The symbol ∀ means:

Element

The symbol ∈ means:

Proper Subset

It is a subset that is not equal to the set it belongs to.

Proper Subset

This symbol ⊂ means:

2ⁿ

The number of subsets of a set with n elements is:

2ⁿ - 1

The number of proper subsets of a set with n elements is:

Venn Diagram

It is a way of visually representing sets of items or numbers by using their logical relationships to decide how they should be grouped together.

The Algebra of Sets

It encompasses the fundamental properties of set operations and set relations.

• Set Complement

• Set Intersection

• Set Union

• Set Difference

• Symmetry Difference

These are the fundamental laws of set algebra:

Set Complement

This symbol (‘or ^c) means:

Set Intersection

This symbol (∩) means:

Set Union

This symbol (∪) means:

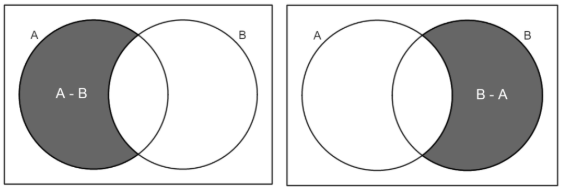
Set Difference

This symbol (-) means:

Symmetric Difference

This symbol (⊕) means:

Set Complement (‘or ^c)

Set Intersection (∩)

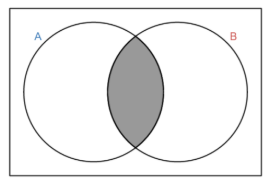
Set Union (∪)

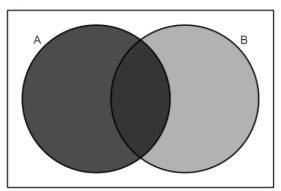
Set Difference (-)

Symmetric Difference (⊕)

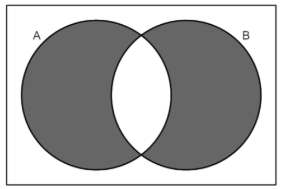
Symmetric Difference (⊕)

A set containing all the elements present in either of the sets but not in their intersection.

Symmetric Difference (⊕)

It is the complement of the sets’ intersection.