Derivative and integral formulas

d/dx [cu]

d/dx [u ± v]

d/dx [uv]

d/dx [u/v]

d/dx [c]

= 0

d/dx [u^n]

d/dx [x]

= 1

d/dx [|u|]

= (u)/(|u|)·(u') (u can't be 0)

d/dx [lnu]

d/dx [e^u]

(e^u)(u')

d/dx [log_a u]

d/dx [a^u]

(ln a)(a^u)(u')

d/dx [sinu]

d/dx [cosu]

-(sinu)(u')

d/dx [tanu]

(sec^2u)(u')

d/dx [cotu]

-(csc^2u)(u')

d/dx [secu]

(secutanu)(u')

d/dx [cscu]

-(cscucotu)(u')

d/dx [arcsinu]

d/dx [arccosu]

d/dx [arctanu]

d/dx [arccotu]

d/dx [arcsecu]

d/dx [arccscu]

∫kf(u)du

k∫f(u)du

∫[f(u) ± g(u)]

∫f(u)du ± ∫g(u)du

∫du

u + C

∫u^n du

((u^(n+1)) / (n+1)) + C

∫(du/u) or u’/u

ln|u| + C

∫e∧u du

e∧u + C

∫a^u du

(1/lna)(a^u) + C

∫sin(u) du

-cos(u) + C

∫cos(u) du

sin(u) + C

∫tan(u) du

-ln|cos(u)| + C

∫cot(u) du

ln|sin(u)| + C

∫sec(u) du

ln|sec(u) + tan(u)| + C

∫csc(u) du

-ln|csc(u) + cot(u)| + C

∫sec^2(u) du

tan(u) + C

∫csc^2(u) du

-cot(u) + C

∫sec(u) tan(u) du

sec(u) + C

∫csc(u) cot(u) du

-csc(u) + C

∫((du)/(√((a^2) - (u^2)))

arcsin(u/a) +C

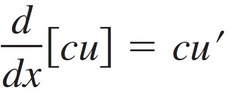
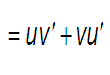
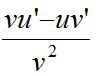
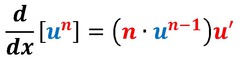
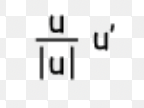
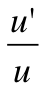
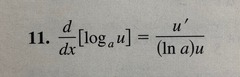
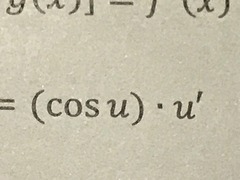
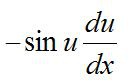
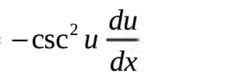
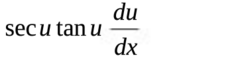
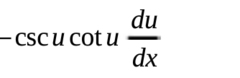
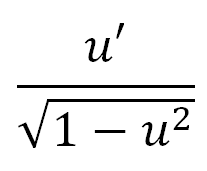
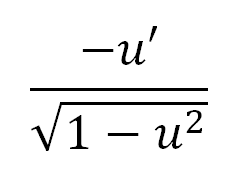
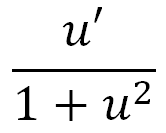
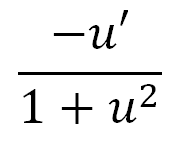
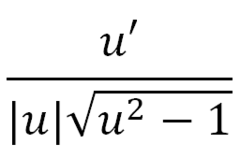
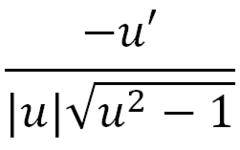
∫((du)/((a^2) + (u^2))

(1/a) arctan(u/a) + C

∫((du)/(u√((u^2) - (a^2)))

(1/a) arcsec(|u|/a) + C

chain rule

d/dx f(u) = f’(u)u’ OR d/dx f(g(x)) = f’(g(x))g’(x)

f’(x) formula

f’(a) formula with x

f’(a) formula with h

∫u dv

uv - ∫v du

logistic equations

dP/dt = kP (M - P), M is carrying capacity. There is the fastest growth when P = 1/2 M

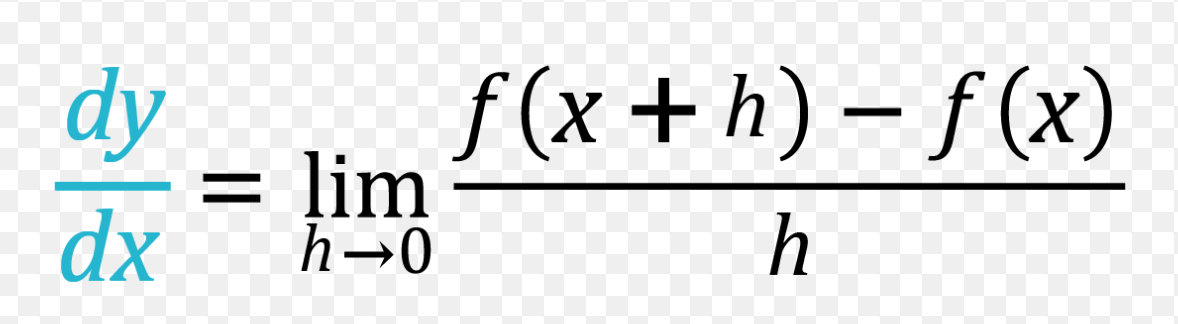
Trig identities

tanx = sinx/cosx, sin^2x + cos^2x = 1, tan^2x = sec^2x -1, 1+cot²x = csc²x

Volume of a disc

\

Volume of a washer

Cross section formula

Fundamental Theorem of Calculus

Start plus accumulation

Second Fundamental Theorem of Calculus

area of trapezoid

A = 1/2 w(h1 + h2)

Riemann Sum

add area of rectangles to get this

Alternate Series Error

error is less than or equal to I a (n+1) I (The next term)

Lagrange error

The f part on top is the maximum between x and c

e^x elementary series

sinx elementary series

cosx elementary series

Taylor series polynomial

not centered at zero

Maclaurin series polynomia

centered at zero

Euler’s setup

Average rate of change (AROC)

slope between two points

Instantaneous rate of change (IROC)

slope at a single point : f’(c)

mean value theorum

find c where m of sec = m of tan, must be continuous on (a,b) and differentiable on (a,b)

average value of a function

average height = area/width

intermediate value theorum

a function f is continuous on (a,b) takes on every y-value between f(a) and f(b)

extreme value theorum

a function f is continuous on (a,b) has both an absolute minimum and an absolute maximum on the interval.

definition of continuity

a function f is continuous at an x-value c if and only the limit as x approaches c(-) of f(x) = the limit as x approaches c(+) of f(x) = f(c).

Squeeze theorum

its at all where x is not equal to c in some interval containing those limits.

arc length

also an integral from a to b: square root of 1 + (f’(x))^2

speed

speed is increased when velocity and acceleration have the same sign

total distance

integral of speed formula

polar area

parametric derivatives

dy/dx is just dy/dt over dx/dt

polar conversions

r^2 = x^2 + y^2

nth term test

geometric series test

p-series

alternating series

integral test

r

ratio test

direct comparison

series with terms smaller than a known convergent series also converges. Series with terms larger than a known divergent series also diverges. Both series must be positive.

limit comparison

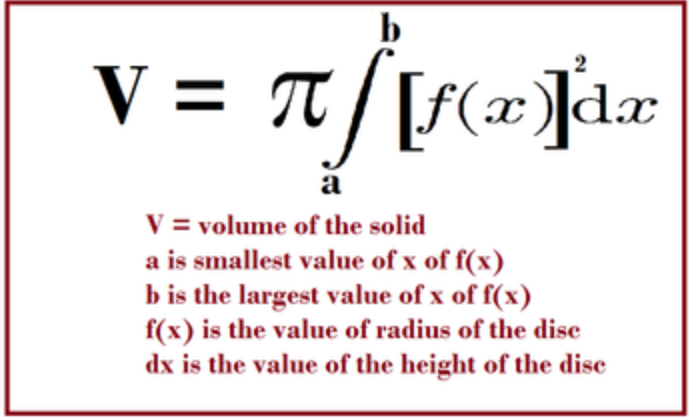
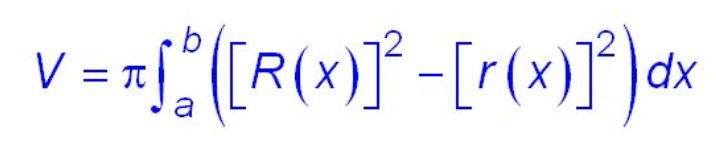
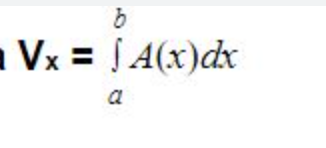
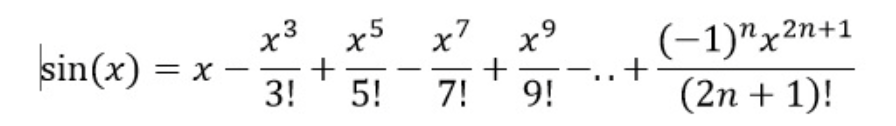
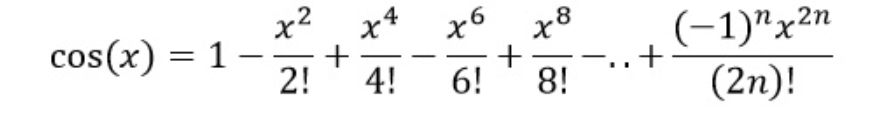
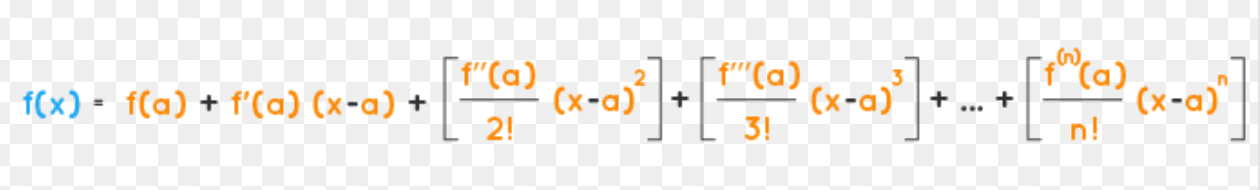
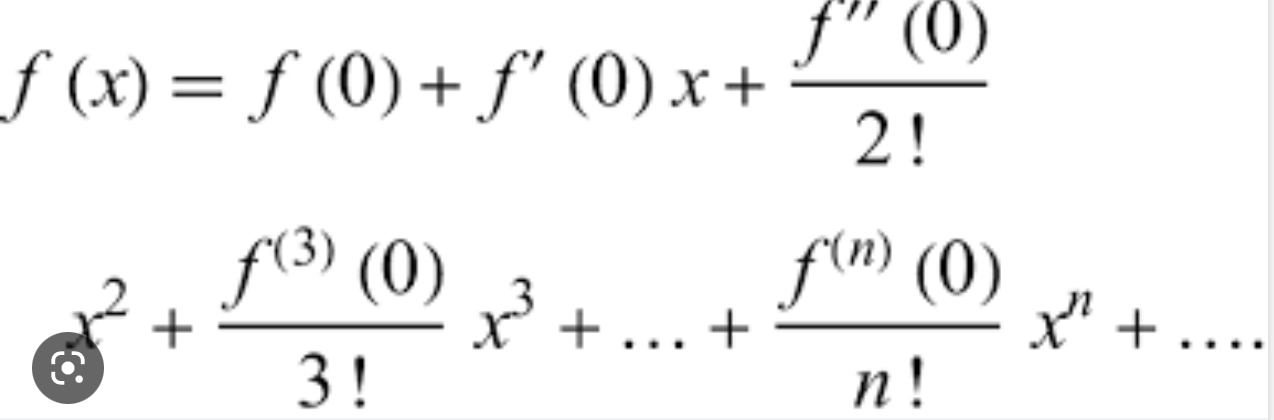
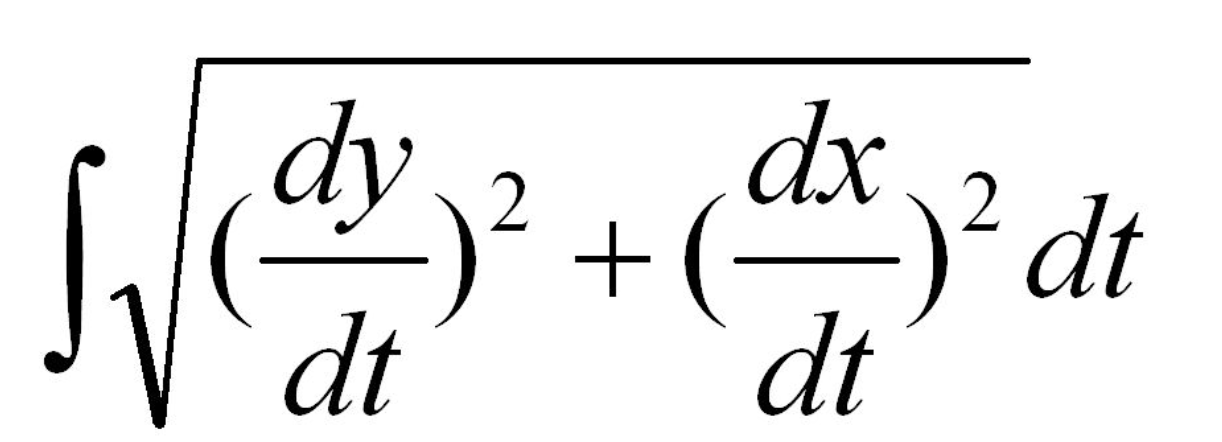
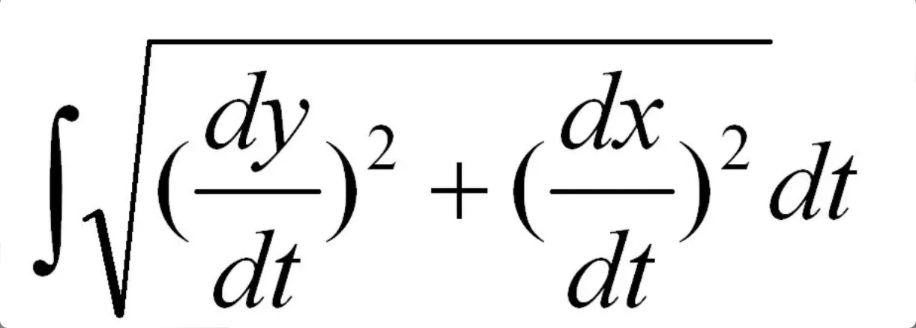
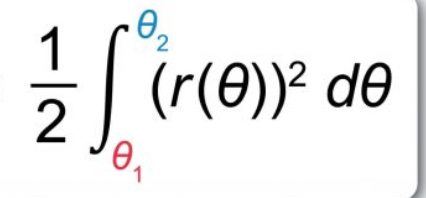
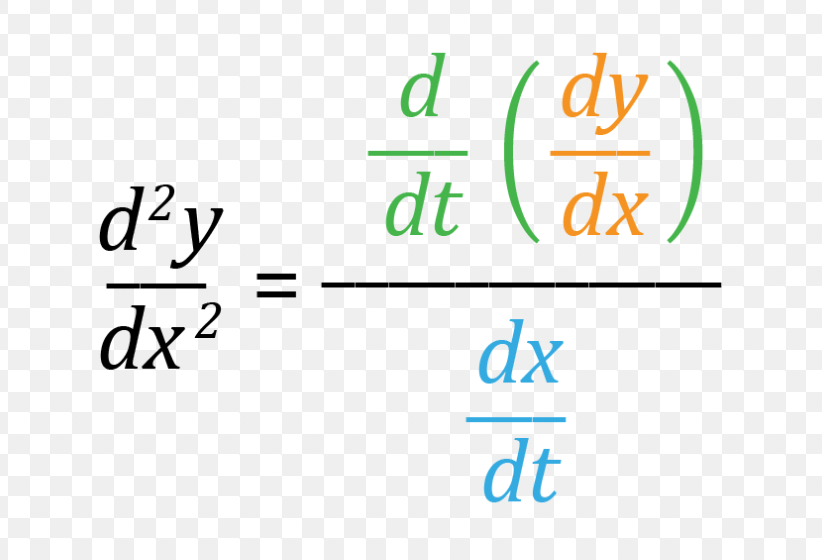
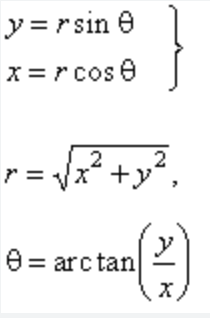
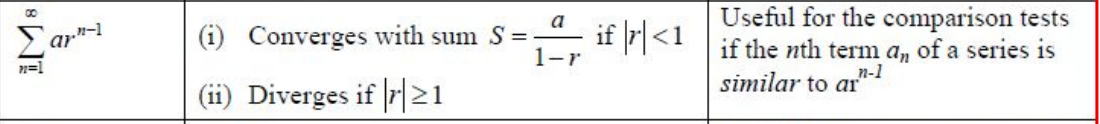
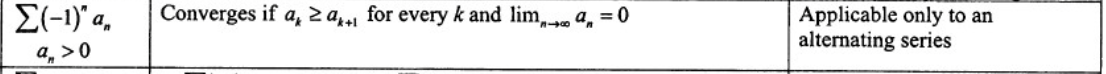
sin2x = …

2sinxcosx

cos2x = ….

cos²x-sin²x OR 1-2sin²x OR 2cos²x - 1

cos²x = ….

(1+cos2x)/2

sin²x = …..

(1-cos2x)/2

if there are odd numbers of a trig function, do what?

save 1 and substitute the even for a trig identity

for even powers of sin and cos, use what?

half angle identities

if sec^n x, n is even and greater than 0, do what…

pull 2 off and save them, replace with trig identity.

if both tan and sec are odd, do what…

save a tanxsecx, tan has to have an odd power for this to work.

trig substitution is done when… (also list the 3 rules)

you are integrating the square root of a quadratic function

1. sqrt(a² - x²) → x =asinθ

2. sqrt(x² - a²) → x =asecθ

3. sqrt(x²+a²) → x=atanθ

even functions

functions that are symmetrical to the y-axis (odd x even = odd, even x even = even, odd x odd = even)

odd functions

functions that are symmetrical to the origin (0,0)