C4 Standing Waves and Resonance

Standing waves and Resonance

C4.1 Standing wave

Produced by 2 waves travelling in opposite direction along same line with same f superposing.
Waves must have same λ and similar A.
They store energy (stationarily), rather than transferring like travelling/progressive waves
Each point on wave oscillates at diffferent speed, overall stationary.
Each point has different A depending on # of superposition herre

C4.2 Node- Antinode

Node: A=0, separated by ^λ/₂ : destructive interference: cancel
Antinode: A=max, also sep. by ^λ/₂: constructive inter.: added A’ds

Fixed positions, only move up down (vertical), dont move along wave

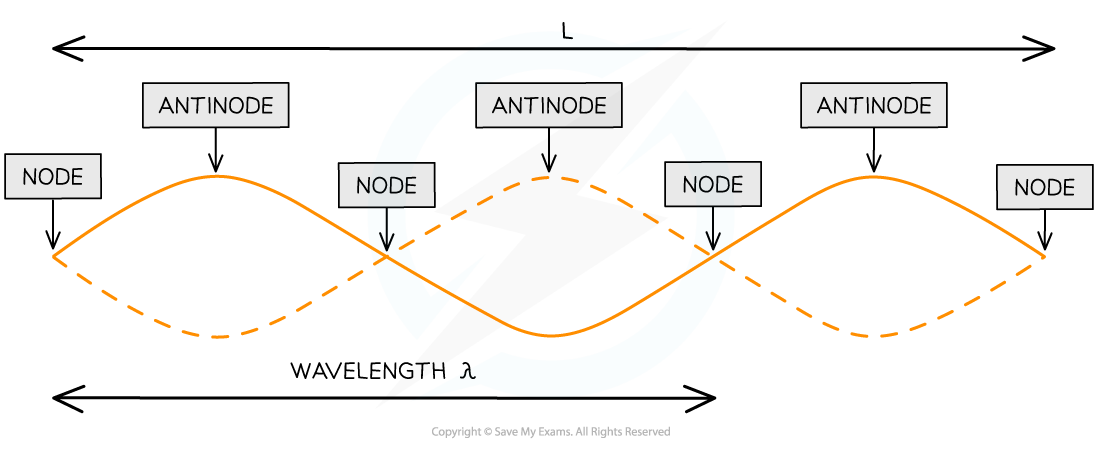
C4.3 Phase on standing wave

In phase: even nr of nodes between - within 1 loop

Anti phase/out of: odd nr of nodes between

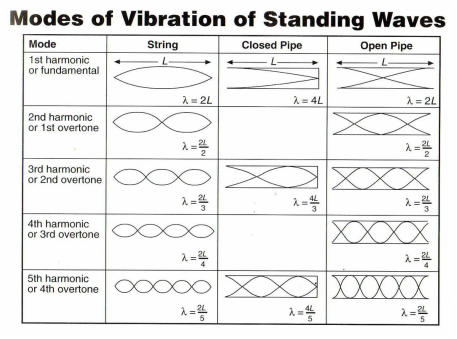
C4.4 Boundaries

Form on strings, in pipes:

nr of nodes depends on: f of producing wave, boundary conditions:
- 2 fixed ends, 2 loose ends, 1free1loose ends

At open end: always antinode
Closed end: alway node

Pipe: longitudinal waves when blowing in an open end; can be 2 fixed ends, 2 loose ends, 1free1loose ends
Guitar: 2x fixed

fixfix: At natural frequency: ^nλ/₂ nodes; ^nλ/₄ full waves.

C4.5 Open closed pipe λ

NOT IN FORMULA BOOKLET — REMEMBERRRR!!!!!
Open-closed: λ = ^4L/_n - n=1,3,5… (n=nr of nodes=harm)

Open-open: λ = ^2L/_n - n=1,2,3…(n=nr of nodes = harmonic)

Closed-closed; λ = ^2L/_n - n=1,2,3… (n=nr of rondjes=harm)

v = fλ

C4.6 Free oscillations vs forced

Free: no transfer of energy to/from surrounding; no external forces on it, vibrates naturally, only internal forces. Free vibration always oscillates at natural/resonant frequency.

Forced: to sustain oscillations in SHM; periodic F must be applied to replace lost energy in damping by resistive forces (friction, drag). Driving force can change frequency of oscillator.

C4.7 Resonance

driving frequency: f - forced
natural frequenct: f_o - f os oscillation when oscillating freely

Resonance = f = f_o → maximum amplitude

C4.8 Damping

Eventually, after driving force stops, all oscillators stop oscillating, as they are damped by external F (drag-friction) acting opposite to motion, reducing the E_k of the oscillator, and turning it into heat

Their amplitudes are decreased, until oscilator is at rest at equilibirum. f and λ are not changing!!

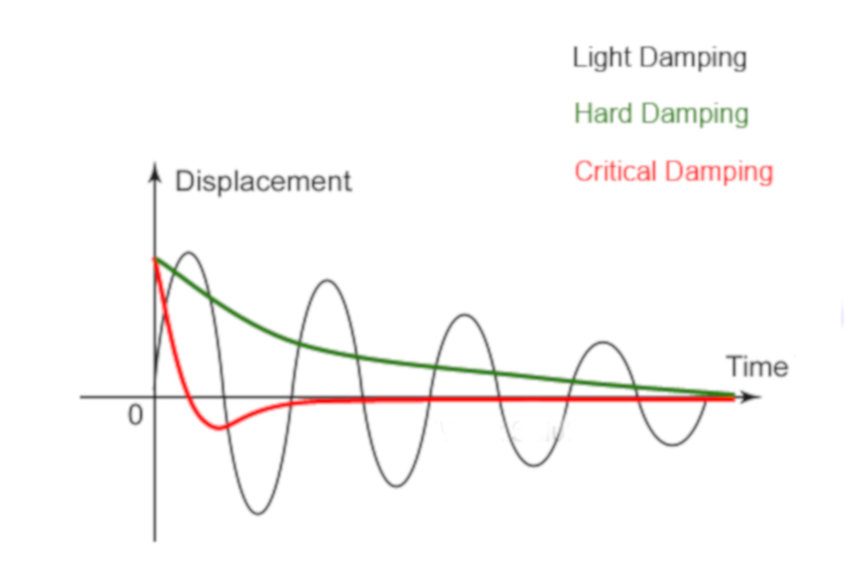
C4.9 Types of damping

Light damping: gradual, exponential decay of A, makes oscill.

Critical damping: return to rest in shortest possible time, no oscillation;

Heavy damping: large resitance; takes ages to go to x=0; door damp