CVEN 365 FINAL REVIEW

Develop a foundation that doesn’t bend when soil moves

Design a stiff, reinforced foundation like a mat or waffle slab to resist bending when the soil moves.

What’s the mohr circle

A graphical representaion of the stresses at one point

What’s the undrained shear strength (Su)? When would it be used?

The shear strength of the soil when it’s not drained. It’s used for slope stability analysis to simulate rapid loading conditions for saturated clays.

3 factors influence soil Modulus (E). What are they?

density, water content, OCR

What is the pole?

The Pole is a point on the Mohr Circle found by drawing a line from a known stress point parallel to the physical plane, helping determine stresses on any other plane.

What’s the preconsolidation process?

The max past effective vertical stress that a soil has experienced

What’s the compressive index (Cc)

The slope of the e - log(o) curve at o’p

What is the coefficient of consolidation (cv)?

measures how fast consolidation (settlement) occurs when water drains out of saturated soil under load.

If it takes 2 years for a 2m height for it to settle, how long will it take for 4m?

Same time (2 years), load does not contribute.

Problem 10.14

A direct shear test is performed on a sample of dry sand. The sample is 50 mm in diameter and 25 mm high and is subjected

to a vertical force of 100 N. At failure, the shear force applied is 60 N, the horizontal movement is 3 mm, and the vertical

movement is 0.5 mm. Calculate the shear strength of the sand and the friction angle, and estimate the dilation angle.

1. A = pir² = (3.14)(25mm)²=1.96×10³ m²

2. Shear strength: Fs/A = (60 N)/(1.96×10^-3) = 30,600 pa = 30.6 kPa

3. Friction angle = tan^-1(Fs/Fn) = tan^-1(60/100)=31

4. Dilation angle = tan^-1(0.5/3)=9.5

Problem 10.16

Two direct shear tests are performed on a sample of saturated clay. The tests are slow tests such that the water stress (pore

pressure) remains equal to zero. The following conditions exist at failure:

Test 1: N = 300N, T = 250N, A = 0.01m2

, S = 100%, uw = 0kPa

Test 2: N = 600N, T = 400N, A = 0.01m2

, S = 100%, uw = 0kPa

where N is the normal force, T is the shear force, A is the sample cross-sectional area, S is the degree of saturation, and uw is

the water stress. Calculate the effective stress cohesion and effective stress friction angle of the clay.

1. Calculate normal and shear stress

   normal stress = N/A

   shear stress = T/A

2. use failure envelope equation

   t = c’ + tan(angle’)

subtract set of equations to get angle:

1. 25 = c’ + tan(angle’)

2. 40 = c’ + tan(angle’)

angle =26.6

3. plug back into falire equation to get c’

   c’ = 10kpa

Assume the same conditions as in problem 10.16 but this time the soil is unsaturated and the readings at failure are as follows:

Test 1: N = 600 N, T = 1900 N, A = 0.01 m2, S = 60%, uw = −400 kPa

Test 2: N = 200 N, T = 900 N, A = 0.01 m2, S = 40%, uw = −300 kPa

where N is the normal force, T is the shear force, A is the sample cross-sectional area, S is the degree of saturation, and uw is

the water tension stress. Calculate the effective stress cohesion and effective stress friction angle of the clay.

1. Calculate normal and shear stress for both tests

   normal stress = N/A

   shear stress = T/A

2. use: o’ = o - S*uw

3. Find the effective stress angle:

   tan(u’) = (t2-t1/o2-o1)

4. Use: t = o’ * tan(u’) + c’ to find the stress cohesion , answer is 2.5 kpa

A medium-stiff clay is tested in an undrained triaxial test. At failure, the effective stress on the failure plane is 230 kPa and

the shear stress on the failure plane is 122 kPa. Calculate the undrained shear strength of this clay.

Su = 122 kpa

Assume: In an undrained triaxial test, friction angle (φu) = 0°.

• This means the shear strength is entirely due to cohesion.

• Undrained shear strength (Su) is equal to the shear stress at failure

Problem 16.6

A soft, saturated clay is tested in an unconsolidated undrained direct shear test with a normal stress of 50 kPa; the shear

strength obtained is 20 kPa. An identical sample is tested, also in an unconsolidated undrained direct shear test, but this time

the normal stress is 100 kPa. What would you expect the shear strength to be?

20 kPa. In undrained conditions, soft clay can't increase effective stress — excess stress is taken by pore water. So, Su stays the same as before:

16.2

A medium dense sand deposit has a dry unit weight of 17kN∕m3, a saturated unit weight of 20kN∕m3, and a friction angle of

32 degrees. Calculate the shear strength (kPa) on a horizontal plane at a depth of 10 m if:

a. The groundwater level is much deeper than 10 m and the sand has no water.

b. The groundwater level is at the ground surface.

c. The groundwater level is at 12 m and the sand is saturated by capillary action.

Use this equation for each case:

tf = c” + (o - aUw)tan(u’)

a. tf = 0 + (10×17 - 0×0)tan(32) = 106.2

b. tf = 0 + (10×20 - 1+10+9.81)tan(32) = 63.7

c. tf = 0 + (10×20 - 1(-2+9.81)tan(32) = 137.2

Problem11.5

For problem 11.4 , use the Pole method to locate the principal stress planes.

1. Plot the failure point (τ = 40, σ′ = 80) on the τ–σ′ graph.

2. Draw the Mohr Circle:

   • Centered at the midpoint of principal stresses

   • Tangent to the failure line (through origin and failure point)

   • From graph: σ1′=144 kPa, σ3′=55 

3. Find the Pole:

   • Draw a line parallel to the stress plane (horizontal plane here) through the failure point.

   • Where it intersects the Mohr circle is the Pole.

4. Draw lines from the Pole to the two ends of the circle (σ′₁ and σ′₃).

   • These lines represent the directions of the principal planes.

5. Read the angles:

   • Angle between failure plane and major principal plane = 31°

   • So, the failure plane is 31° from σ₁′ direction, or 59° from σ₃′

---

Key Results:

• Principal stresses:

  • σ1′==144 kPa

  • σ3′=55 kPa

• Principal planes are at 31° and 59° from the horizontal plane.

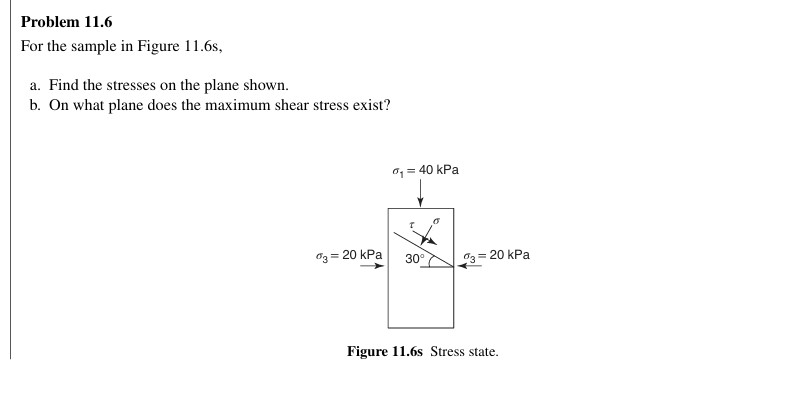
b. To find the plane where the maximum shear stress acts, use the Pole method. First, draw a line parallel to the plane of σ1\sigma_1σ1​ (horizontal) — this line intersects the Mohr circle at the stress point and the Pole. Then, draw a line from the Pole to the top of the Mohr circle. This 45° line shows the plane of maximum shear stress (see Figure 11.8s).

What are the two main phases in running a triaxial test?

With respect to drainage during each one of these two phases, what are the different types of tests that can be run?

For each type of test, what parameters can you obtain from the data?

• The two main phases are:

  1. Consolidation phase

  2. Shearing phase

• Based on drainage during these phases, there are three types of triaxial tests:

  • UU (Unconsolidated Undrained): No drainage in either phase
    → Gives: Undrained shear strength, strain at failure, and undrained modulus

  • CU (Consolidated Undrained): Drainage during consolidation, but not during shearing
    → Gives: Effective friction angle (𝜙′) and cohesion (c′) if pore pressure is measured

  • CD (Consolidated Drained): Drainage allowed in both phases
    → Gives: Effective 𝜙′, c′, and drained modulus

What is consolidation?

Consolidation is when water slowly squeezes out of wet soil (like clay) after it's loaded, causing the soil to shrink and settle over time.

Example:
If you build a building on soft clay, the weight pushes water out of the soil slowly, and the ground sinks a little over time — that’s consolidation.

10.26 (same as 10.25)

Two CU triaxial tests are performed on a sample of unsaturated clay. At failure, the results are as follows:

Test 1: 𝜎3 = 20 kPa, 𝜎1 = 190 kPa, S = 60%, uw = −100 kPa

Test 2: 𝜎3 = 60 kPa, 𝜎1 = 450 kPa, S = 50%, uw = −300 kPa

where 𝜎3 is the total confinement stress, 𝜎1 is the total vertical stress at failure, S is the degree of saturation, and uw is the

water stress.

a. Calculate 𝜎3, 𝜎1, 𝜎′3, and 𝜎′1, at failure.

b. Draw the Mohr circle at failure in the 𝜏 vs. 𝜎′ set of axes.

c. Draw the failure envelope and find the effective stress strength parameters c′ and 𝜙′.

a. o3 = 20, o1 = 190

o’3 = o3-Suw

o’1 = o1-suw

(repeat for test 2)

b. plot circle and failure line, which is line tangent to circles

c. use equation t = o*tan(u’)+c’

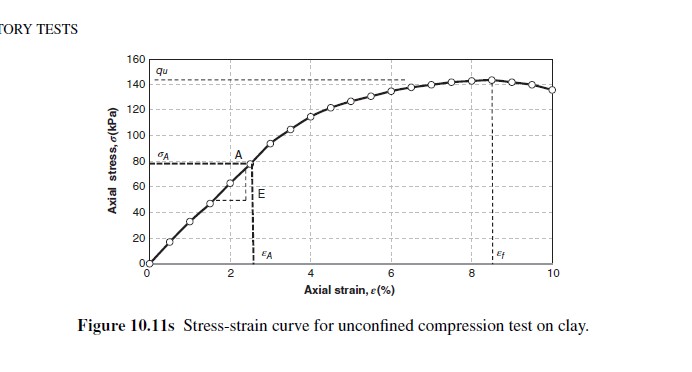
Problem 10.21

An unconfined compression (UC) test on a sample of clay gives the stress-strain curve shown in Figure 10.11s. Calculate the

undrained shear strength and the UC modulus for this sample. What geotechnical problem do you think this undrained shear

strength and this modulus could be used for?

From Figure 10.11s, we can determine that the maximum axial stress qu is 144 kPa. The axial strain at failure is 8.5%. The

undrained shear strength is half of the maximum axial stress: su = qu/ 2 = 144/ 2 kPa = 72 kPa. The UC modulus can be obtained

from the straight portion of the stress-strain curve for this sample. The following equation shows the UCmodulus calculations.

E = 𝜎A

𝜖A = 78 kPa/ 0.025 = 3120 kPa = 3.12 MPa

Problem 10.24

A triaxial test with water stress (pore-pressure) measurements is performed on a sample of saturated silty crushed rockfill and

gives the results shown in Figure 10.51. The total confining stress is 35 kPa.

a. Calculate the total stress secant modulus E and the effective stress secant modulus E′ for a vertical strain equal to 0.2%,

0.5%, 1%, 2%, 3%, 4%, and 5%. Then plot the curve giving the soil modulus both as a function of strain and as a

function of log strain.

b. At failure, the vertical effective stress is 100 kPa. Calculate the effective stress friction angle of the sand if the effective

stress cohesion c′ is zero.

1. The total stress secant modulus E can be obtained.

E = (𝜎1 − 2v𝜎3) ∕ 𝜀

Undrained: v = 0.5, drained; v= 0.35

2. look at table

3. The effective

   stress secant modulus E′ can then be obtained.

   E′ = (𝜎′1 − 2v′𝜎′3) ∕𝜀

4. Assuming that the effective cohesion is 0, the effective stress friction angle can be obtained from the Mohr circle using the effective principal stresses at failure (Figure 10.17s): 𝜙′ = 47.5∘.

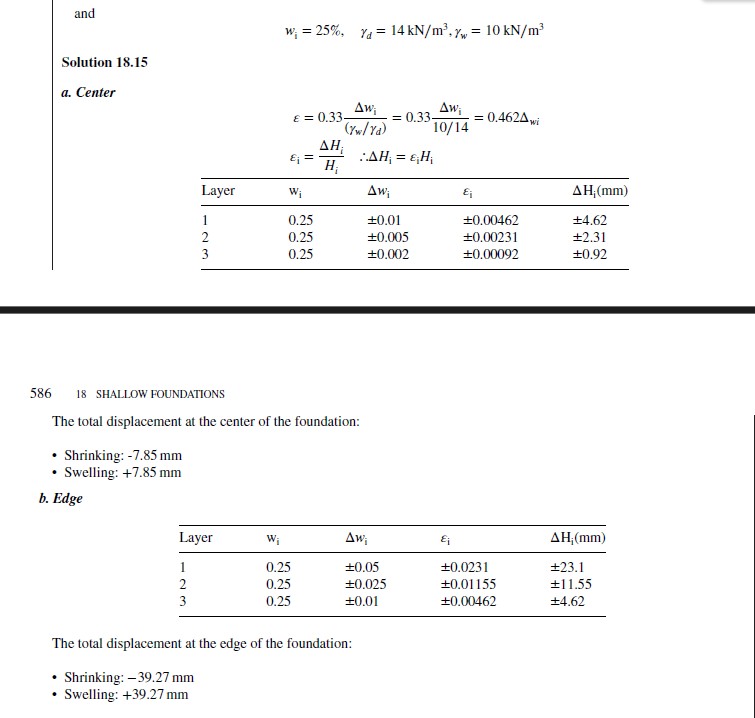
Problem 18.11

In 1955, an oil tank 10m high and 38m in diameter is built as shown in Figure 18.10s.

a. Calculate the settlement of the center of this tank (point C on Figure 18.10s) using the data from Figure 18.11s. Assume that the stress increase in the middle of the compressible layer is equal to the pressure under the tank because the layer is shallow and thin. In 1975, this tank is removed; a year later, a new tank 15m high and 76m in diameter is built. The edge of the new tank goes through the center of the old tank.

b. Calculate the settlement of the edge of the new tank away from the old tank (point B on Figure 18.10s) using the data from Figure 18.11s. Assume that the stress increase at the edge of the new tank in the middle of the compressible layer is equal to one half of the pressure under the new tank.

c. Calculate the settlement of the edge of the new tank that passes over the center of the old tank (point C on Figure 18.10s) using the data from Figure 18.11s. Make the same assumption as in b.

d. Do you see any problem with the difference in settlement between C and B for the new tank?

look in textbook (activ recall cuz it’s long to put in here.)

Write the 6 equations of elasticity

4.5.6 (Txy/G), (Tyz/G), Tzx/G)

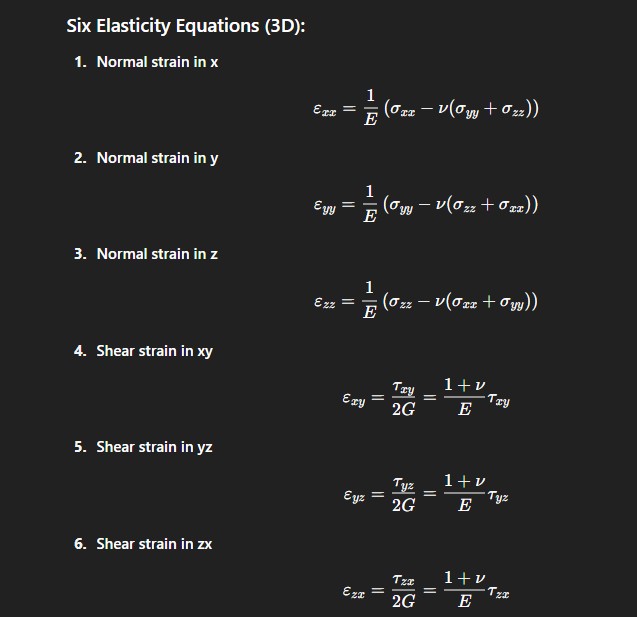
Recompression index

The slope of the e log(o’) curve before the pre consolidation pressure.

What kind of foundation is best shrink swell soil

stiffened slab on grade

What’s the effetcive stress

o’ = o - aUw

How do you get the modulus from the triaxial test where u measure o1,o3,etc

E = (o1-2v)o3/e1

What’s the shear strength on failure plane?

s = c’ + (o - aUw)tan(o”)

Why do we need 2 triaxial tests?

shear strength has 2 unknowns to find cohesion and effective angle