Topic 3 - Bonding: Mastery ~ Theories and Hybridization

Limitations of Lewis Structures

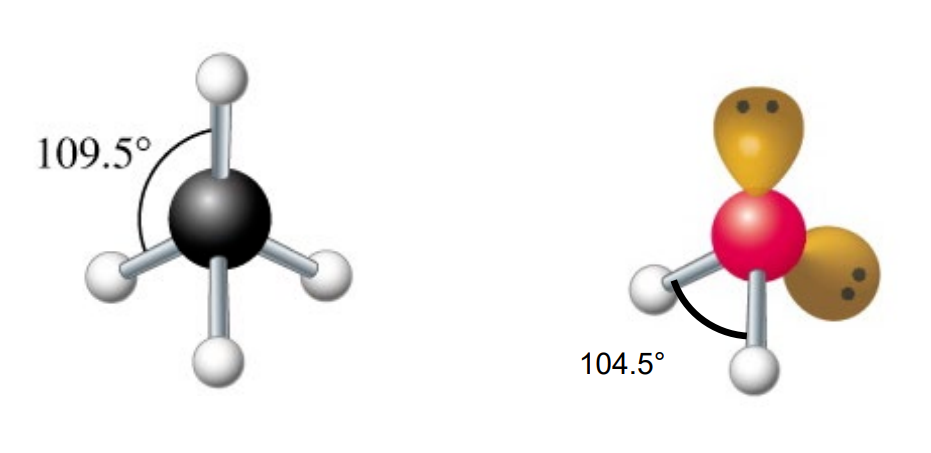
• They do not provide a 3D shape; VSEPR (Valence Shell Electron Pair Repulsion) theory is needed to determine molecular shape and bond angles.

• They don't explain why different bonds have different properties or what type of bond exists, which relates to reactivity.

• They cannot fully account for electron-deficient compounds like diborane (B₂H₆), where there aren't enough electrons to make typical bonds and satisfy the octet rule.

• Doesn't account for the paramagnetism of molecules like O₂.

  • The Lewis structure for O₂ is O=O (a double bond), which predicts all electrons paired.

  • If that were correct, O₂ would be diamagnetic (no unpaired electrons).

  • But experiments show O₂ is paramagnetic (it is attracted to a magnetic field), meaning it has unpaired electrons.

  • The lewis structure doesn't account for MOs.

• They struggle with molecules having multiple valid structures, known as resonance structures.

• Lewis diagrams provide an image of bonding and non-bonding valence electrons and give an indication of bond order, but not numerical values for bond lengths or strengths.

VSEPR Theory

• VSEPR theory uses Lewis structures and is based on the idea that pairs of electrons (in bonds and lone pairs) repel each other.

• The molecular shape is governed by the optimal arrangement that places electrons as far from one another as possible.

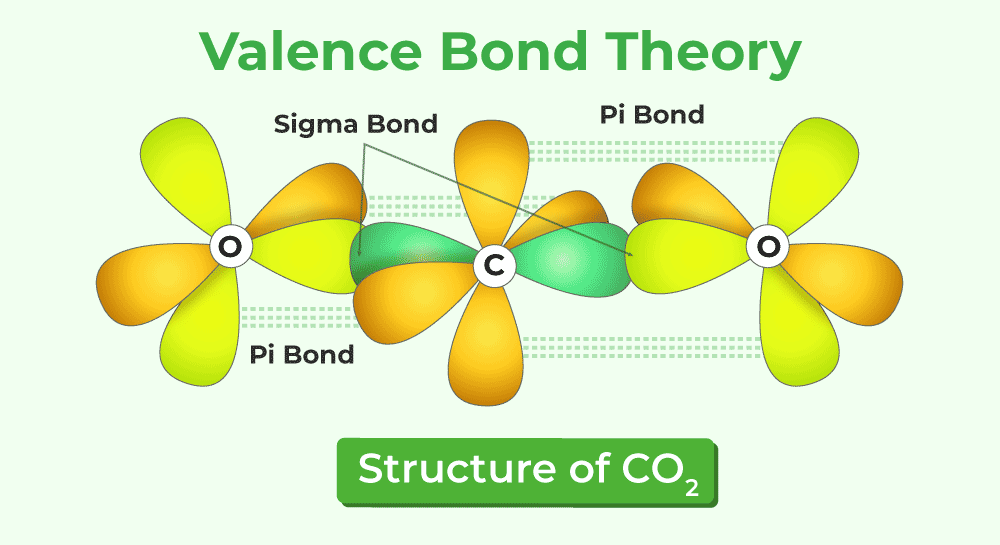
Valence Bond Theory (VBT)

• VBT uses orbital overlap to describe bonding. Different ways of overlapping result in different types of bonds.

• It explains the type of bonding (σ or π) and, in part, different reactivities due to different orbital energies.

• Orbitals have specific orientations in space, which can potentially explain molecular shapes.

• VBT provides a justification for shapes predicted by VSEPR.

Hybridization

• Orbitals can combine to produce new orbitals on the same, single atom. This process is called hybridization.

  • Different from molecular orbitals; While molecular orbitals form from inter-atom orbital overlap, hybrid orbitals form from intra-atom orbital overlap. Hybrid orbitals explain bond angles and shapes of molecules, while molecular orbitals explain bond order, magnetism, etc.

•  If n atomic orbitals combine, n new hybrid orbitals are produced.

Determining Hybridization

The amount of electron domains = the number of hybrid orbitals and determines the hybridization

• 2 domains = sp

• 3 domains = sp²

• 4 domains = sp³

*Remember, the core electrons may not be shown but it is part of the total amount of electron domains too.

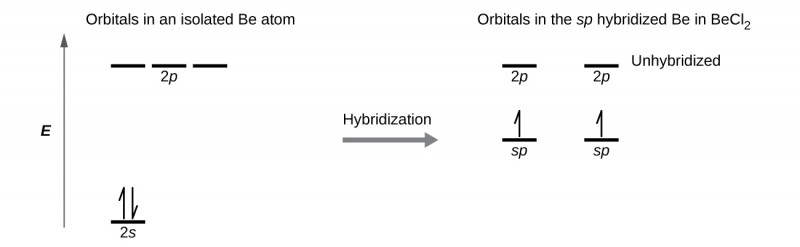
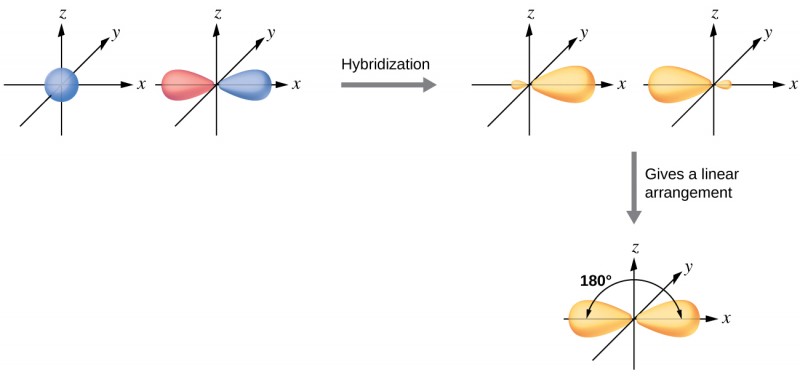
Hybridization - sp Hybridization

• Combines one s orbital and one p orbital to produce two sp orbitals.

• The two sp orbitals are oriented together, 180° apart, resulting in a linear shape.

• Leaves two p orbitals behind (because each main shell has 3 p orbitals (p_x, p_y, p_z)), which can form two π bonds.

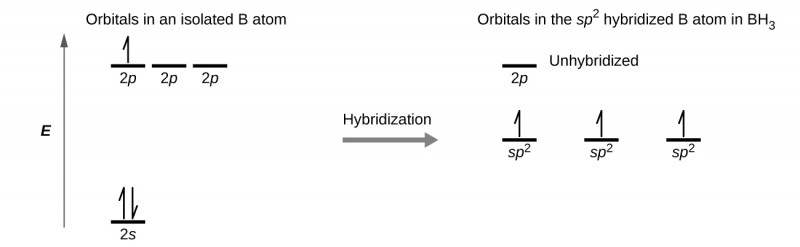
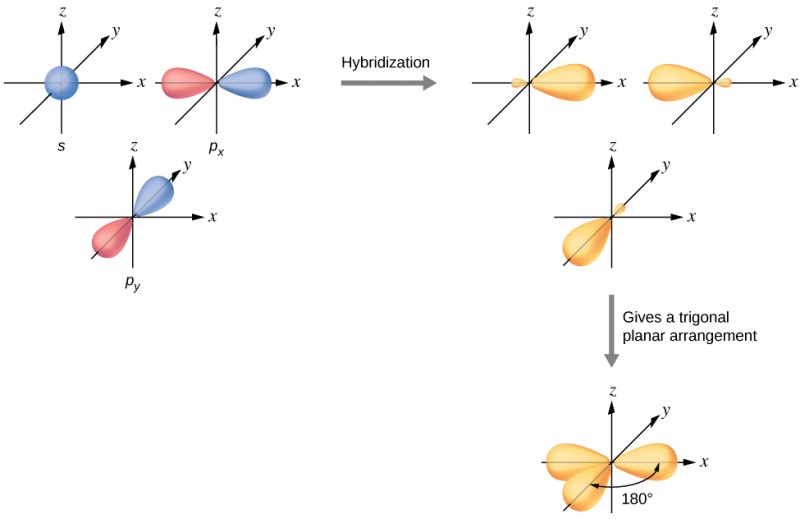
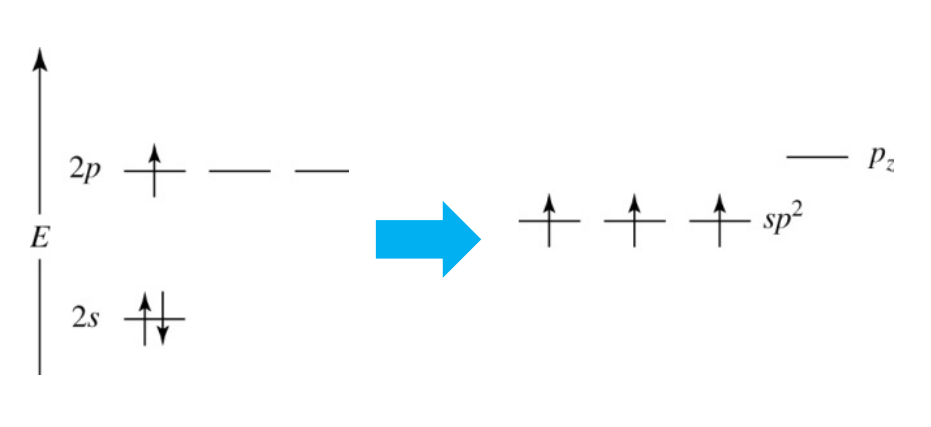
Hybridization - sp² Hybridization

• Combines one s orbital and two p orbitals to produce three sp² orbitals.

• The three sp² orbitals are 120° apart, resulting in a trigonal planar shape.

• Leaves one p orbital behind (because each main shell has 3 p orbitals (p_x, p_y, p_z)), which can form a single π bond.

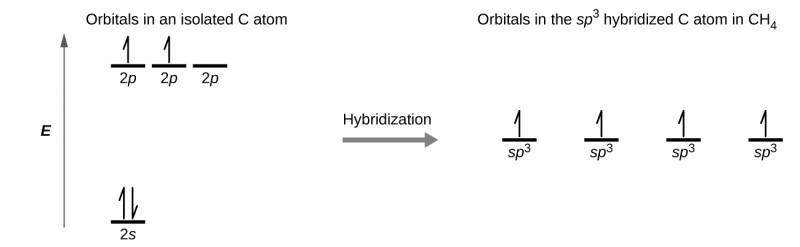
Hybridization - sp³ Hybridization

• Combines one s orbital and three p orbitals to produce four sp³ orbitals.

• The four sp³ orbitals are approximately 109.5° apart, resulting in a tetrahedral shape.

• Leaves no p orbitals behind (because each main shell has 3 p orbitals (p_x, p_y, p_z)), thus no ability to form π bonds.

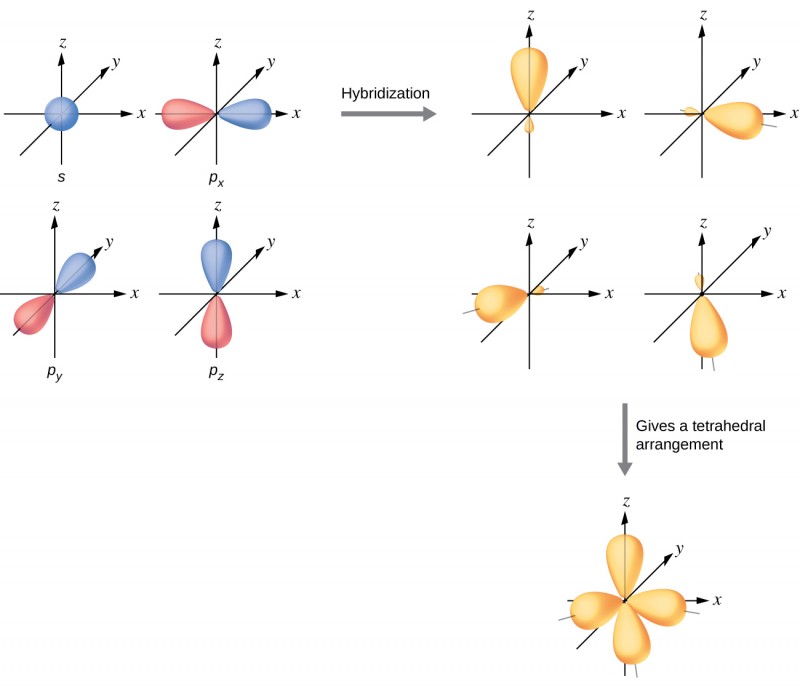
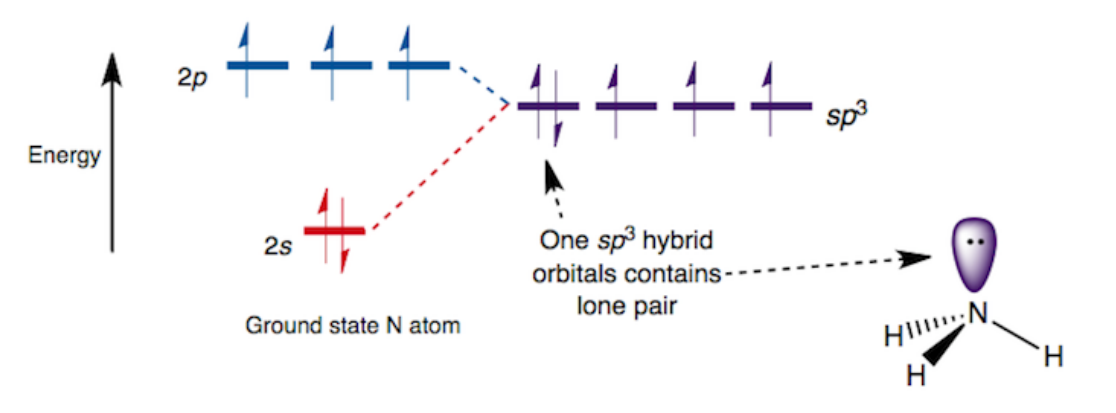
Hybridization and Lone Pairs

• Lone pairs still occupy an orbital, typically a hybrid orbital

• Lone pairs repel more than bonding pairs, affecting bond angles

Hybridization and Empty Orbitals

Empty orbitals are not used in hybridization.

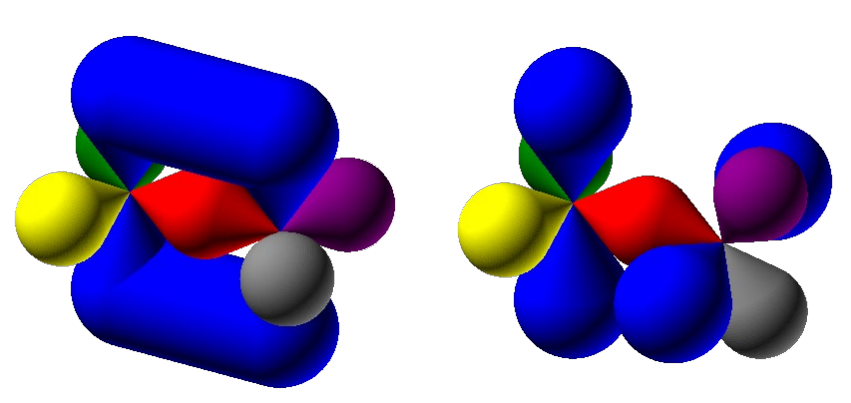
Multiple Bonds Via Hybridization

• Double Bonds: When each atom is sp² hybridized, each atom is left with one unhybridized p orbital. These two atoms overlap side-to-side to form a π bond, in addition to the σ bond formed by sp^2-sp² overlap.

• Triple Bonds: When each atom is sp hybridized, each atom is left with two unhybridized p orbitals. These two atoms overlap side-to-side to form two π bonds, in addition to the σ bond formed by sp-sp overlap.

 

*Rotation around π bonds requires breaking them, preventing changes in atom positions

*The leftover sp or sp² orbitals not involved in inter-atom σ bonding just form σ bonds with another atom, not in this particular bond

Resonance Structures

• Resonance structures: For some molecules, several valid Lewis structures can be drawn, differing only in the placement of electrons (single bonds, double bonds, triple bonds).

  • They show how electrons could be arranged, but none of them alone represent the real molecule.

 

• Bond Length: These structures imply different bond lengths, as single, double, and triple bonds have different lengths.

• But experiments show equal bond lengths that are intermediate (the average) between the single and double bonds.

• This real structure is a resonance hybrid of these Lewis structures; it is a single, weighted average of all resonance structures.

Resonance Structure - Representation

Resonance structures can be represented with a dashed bond, which represents delocalized electrons.

• Delocalization is when electrons are not confined to a single bond or atom, but instead are spread out (shared) over several atoms in a molecule.

• Usually involves π electrons (from double bonds) or lone pairs that can overlap with adjacent p orbitals.

 

Molecular Orbital (MO) Theory

• MO theory was developed to overcome the deficiencies of Lewis and VBT, explaining electron-deficient and paramagnetic compounds.

• It is based on atomic orbitals (AOs) combining to produce molecular orbitals (MOs).

• When n AOs combine, they produce n MOs, some bonding, some anti-bonding, and some non-bonding.

• MOs consider the entire molecule at once, allowing for large orbitals that span a significant portion of the molecule, explaining delocalization

Molecular Orbital (MO) Theory - Bond Order (BO)

Formula: BO = (total # bonding electrons - total # anti-bonding electrons) / 2.

• Gives the amount of bonds between 2 atoms over the entire molecule

• Correlates positively with bond enthalpy (strength) and negatively with bond length.

• A BO of 0 indicates the molecule is unstable and unlikely to exist. If it exists, it may be unstable.

Molecular Orbital (MO) Theory - Electron Configuration

Specified similarly to atomic orbitals

Example: H₂ - 1σ²

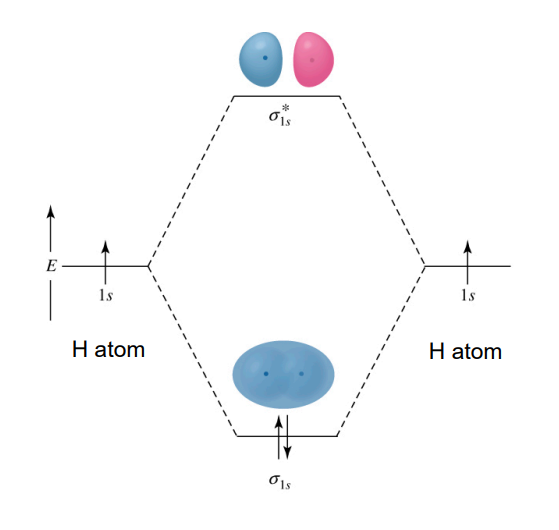
Molecular Orbital (MO) Theory - Limitations

• Very time-consuming.

• For anything larger than hydrogen, it is still an approximation.

• Properties observed from MO theory can guide understanding when using simpler models like Lewis structures and VBT.

Homonuclear Diatomics (in the 2nd Period)

• Homonuclear = made of the same element.

• Diatomic = two atoms.
  So a homonuclear diatomic molecule is a molecule consisting of two identical atoms.

• For the 2nd period (Li → Ne), the possible homonuclear diatomics are:
  Li₂, Be₂, B₂, C₂, N₂, O₂, F₂, Ne₂.

Molecular Orbital (MO) Theory - Filling

• After filling the bonding and anti-bonding (σ and σ*) MOs for 1s and 2s: 

  • 2p orbitals form σ and π orbitals

    • Each atom has three 2p orbitals: 2p_x, 2p_y, 2p_z.

    • When two atoms approach, they combine to form molecular orbitals:

      • σ(2p_z) (head-on overlap along internuclear axis)

      • π(2p_x) and π(2p_y) (side-on overlap, degenerate pair)

      • σ*(2p_z) (antibonding)

      • π*(2p_x), π*(2p_y) (antibonding, degenerate pair)

  • So in total, the 2p set produces 6 molecular orbitals:
    σ(2pz), π(2p_x), π(2p_y), σ*(2p_z), π*(2p_x), π*(2p_y).

Molecular Orbital (MO) Theory - For Homonuclear Diatomics (2nd Period)

• n polyatomic molecules (like CH₄), use Valence Bond Theory (VBT) and hybridization (sp, sp², sp³, …) to explain bond angles and shapes in 3D.

• In homonuclear diatomics, there are only two atoms on one axis.
  → Hybridization isn’t needed, because there’s no need to mix orbitals to make angled bonds.
  Instead, orbitals just overlap directly along the axis between the two atoms.

• This is because homonuclear diatomics have points of inversion

  • A point of inversion (i) is a symmetry element; hence the midpoint between the two nuclei of the two atoms is the inversion centre.

Molecular Orbital (MO) Theory - For Homonuclear Diatomics (2nd Period): Gerade and Ungerade

Gerade (g) vs. ungerade (u): Quirk that only shows up in homonuclear diatomics

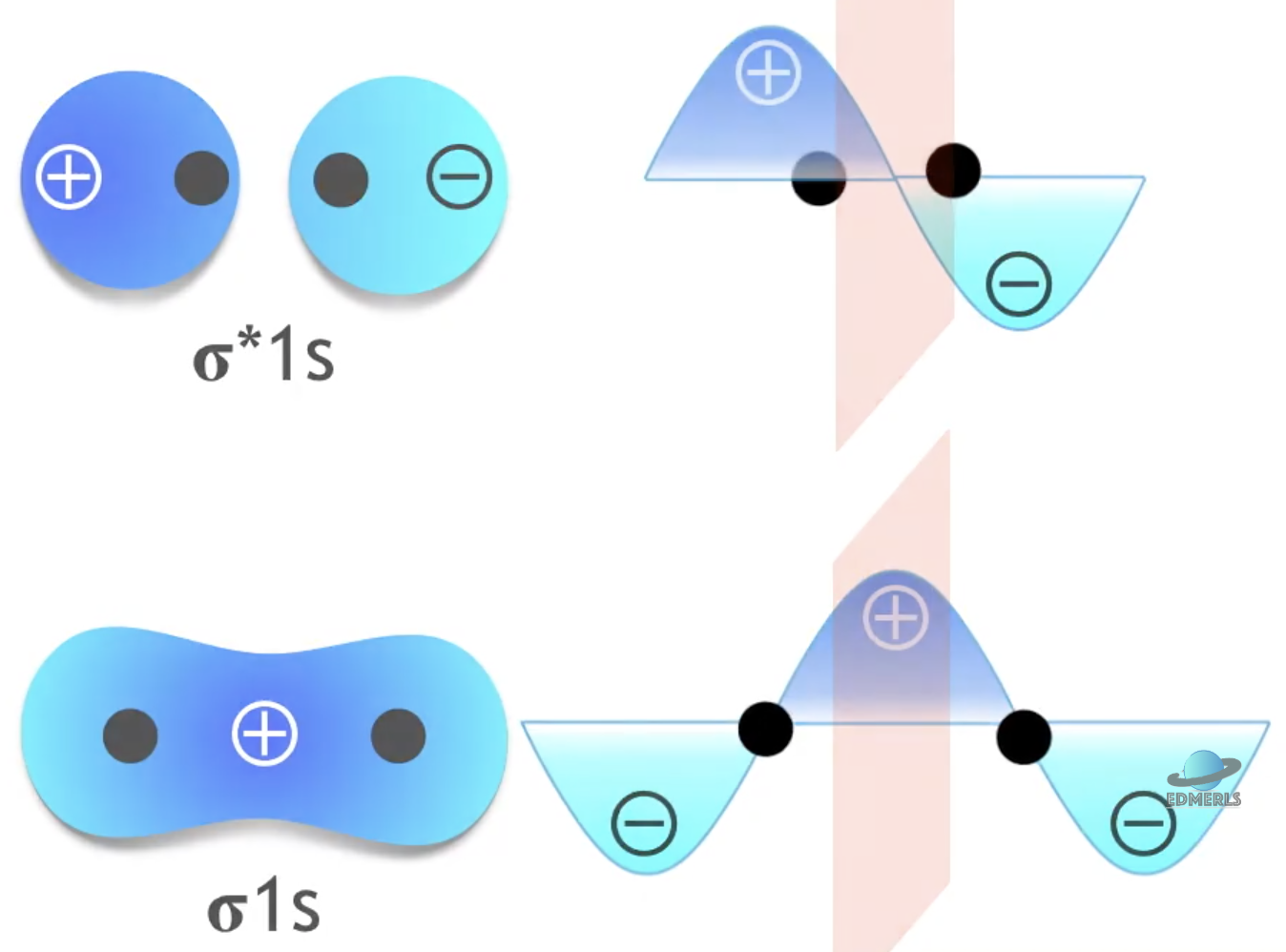
• Gerade (g = “even”): The orbital does not change sign under inversion.

  • Example: σ(1s) bonding orbital in H₂.

• Ungerade (u = “uneven”): The orbital changes sign (ψ → –ψ) under inversion.

  • Example: σ*(1s) antibonding orbital in H₂.

 

Gerade vs. Ungerade of MOs:

• For σ orbitals (from s-s or p_z-p_z overlap along the axis):

  • Bonding (constructive) → gerade

  • Antibonding (destructive) → ungerade

• For π orbitals (from p_x-p_x/p_y-p_y side-on overlap):

  • Bonding (constructive) → ungerade 

  • Antibonding (destructive) → gerade

 

Naming Scheme:

• Number (1, 2, 3, …) = which level it is in that symmetry/type (lowest = 1, then up).

• Letter (σ or π) = type of orbital (end-on vs side-on overlap).

• g/u = symmetry under inversion (gerade/ungerade).

 

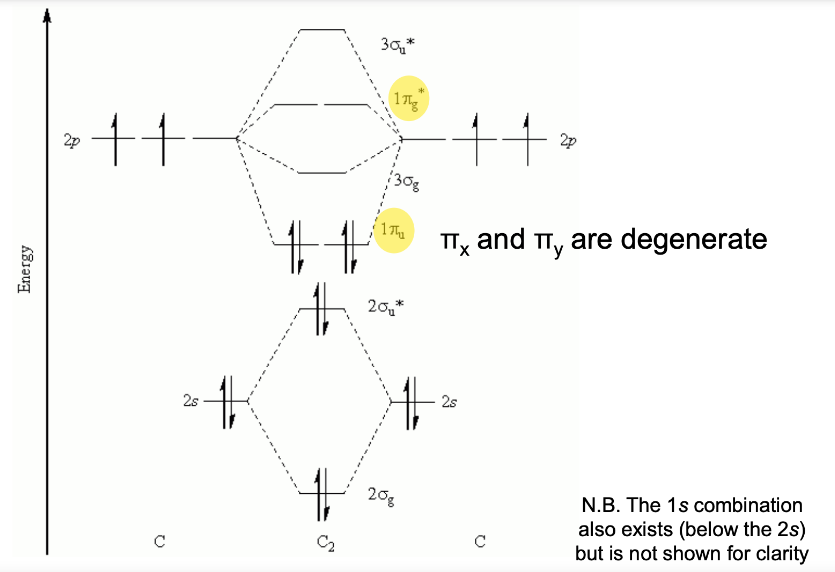
Molecular Orbital (MO) Theory - For Homonuclear Diatomics (2nd Period): Orbital Mixing

From the three atomic 2p orbitals:

• σ(2p_z) → from head-on overlap along the internuclear axis.

• π(2p_x), π(2p_y) → from side-on overlap.

• Antibonding versions (σ* and π*).

 

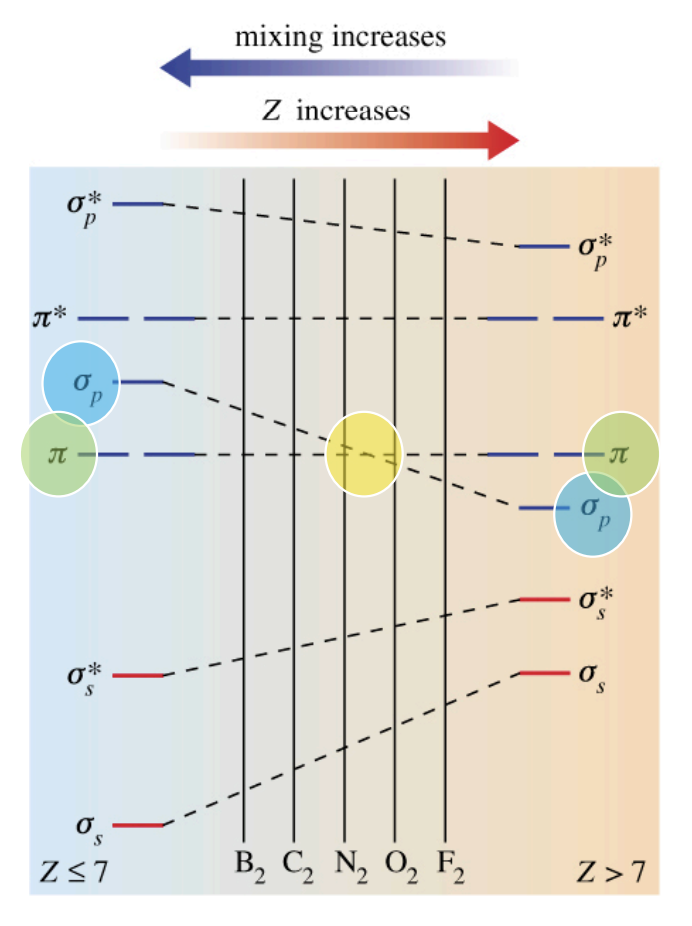
Initially, for lighter 2nd-period elements, the π MOs formed from p-orbitals are lower in energy than the σ MOs from p-orbitals, and gets filled first...

• Orbital Mixing: The 2s and 2p orbitals have similar radii and can interact ("mix").

  • This mixing primarily affects the σs and σp MOs: it stabilizes σs and destabilizes σp, making their energy levels further apart.

  • As you move across the 2nd period, the 2s and 2p orbitals become further apart in energy.

  • Eventually (around oxygen), the separation is enough that the σ2p MO becomes lower in energy than the π2p MO. This explains why liquid O2 is paramagnetic (it has unpaired electrons in the higher-energy π* orbitals)

  • So the filling order starts to change in the heavier 2nd-period elements:

    • B₂, C₂, N₂: electrons go into π(2p_x), π(2p_y) before σ(2p_z). 

    • O₂, F₂, Ne₂: electrons go into σ(2p_z) before π(2p_x), π(2p_y).

 

• Summary

  • For Z ≤ 7 (B, C, N) → π(2p_x), π(2p_y) fill first.

• For Z ≥ 8 (O, F, Ne) → σ(2p_z) fills first

Homonuclear Diatomics (in the 2nd Period) for Spectroscopy 

Useful concepts in spectroscopy and reactivity!

 

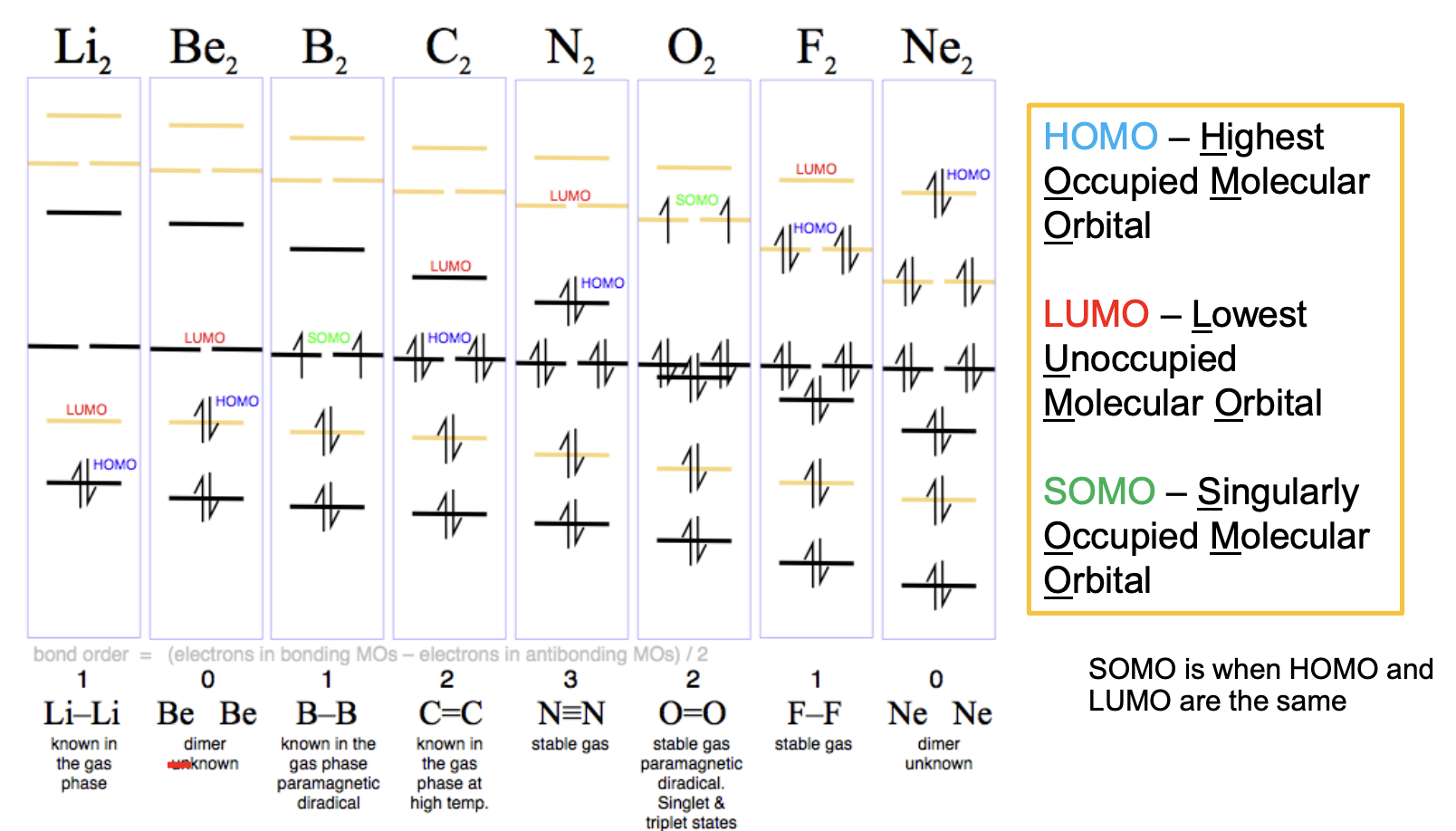
1. HOMO

• Highest Occupied Molecular Orbital.

• The “top filled orbital” in the MO diagram.

• Chemically, it’s the orbital that’s most available to donate electrons (e.g. in nucleophilic reactions, or photoemission).

 

2. LUMO

• Lowest Unoccupied Molecular Orbital.

• The first empty orbital above the HOMO.

• It’s the orbital most likely to accept electrons (e.g. in electrophilic attack, or electronic excitations).

 

3. SOMO

• Singly Occupied Molecular Orbital.

• Happens when you have an unpaired electron in the HOMO.

• Key in radicals and paramagnetic species.

• Example: in O₂, the HOMO is actually a pair of degenerate SOMOs (the two unpaired electrons in the π* orbitals).

 

4. Why do they matter?

• HOMO–LUMO gap = energy difference between HOMO and LUMO → determines optical/electronic properties (color, conductivity, reactivity).

• In photochemistry, excitation means promoting an electron from the HOMO → LUMO.

• In reactivity:

  • HOMO = electron donor orbital.

  • LUMO = electron acceptor orbital.

  • SOMO = special case → radicals react differently because of them.

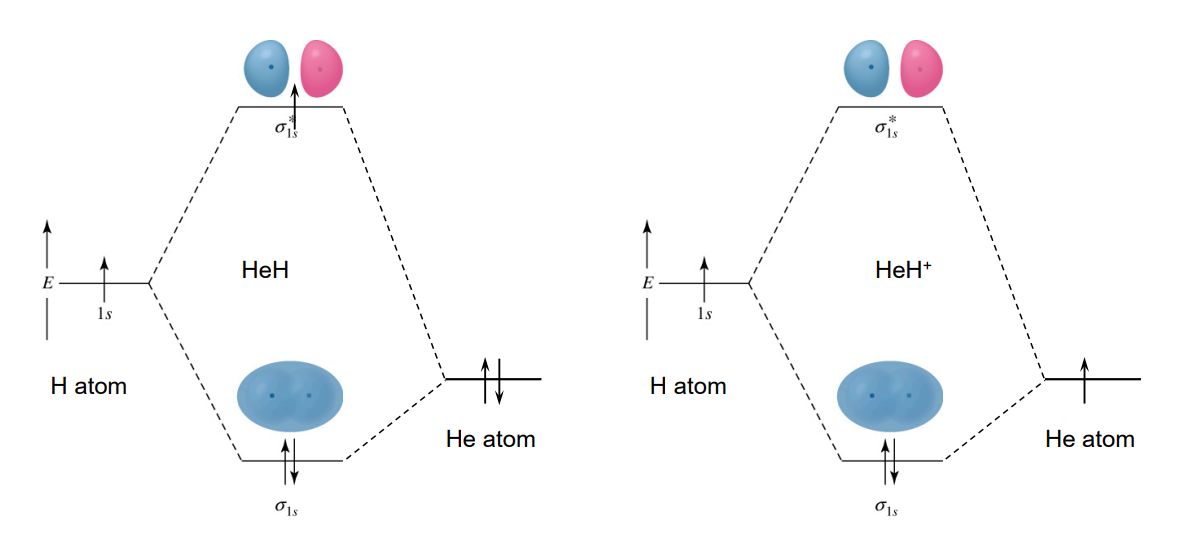
Heteronuclear Diatomics vs. Polyatomics

• Heteronuclear Diatomics: follow the same principles as homonuclear diatomics, but the diagrams are more complicated.

• Polyatomics: MOs spread over all atoms, meaning electron pairs in bonding MOs help bind the entire molecule. Some polyatomic MOs are equally delocalized, others are unevenly distributed.