Set Theory and Relations: Key Concepts for Discrete Mathematics

Sets

set is a collection of unique or distinct elements

ex :

A = { 1,2,3,5}

not ex:

B= {1,2,2,3} ; however, it is a BAG

Partition

a partition on a set A is a collection of A whose union is A

Partition example

Powerset

the set of all subsets of a set

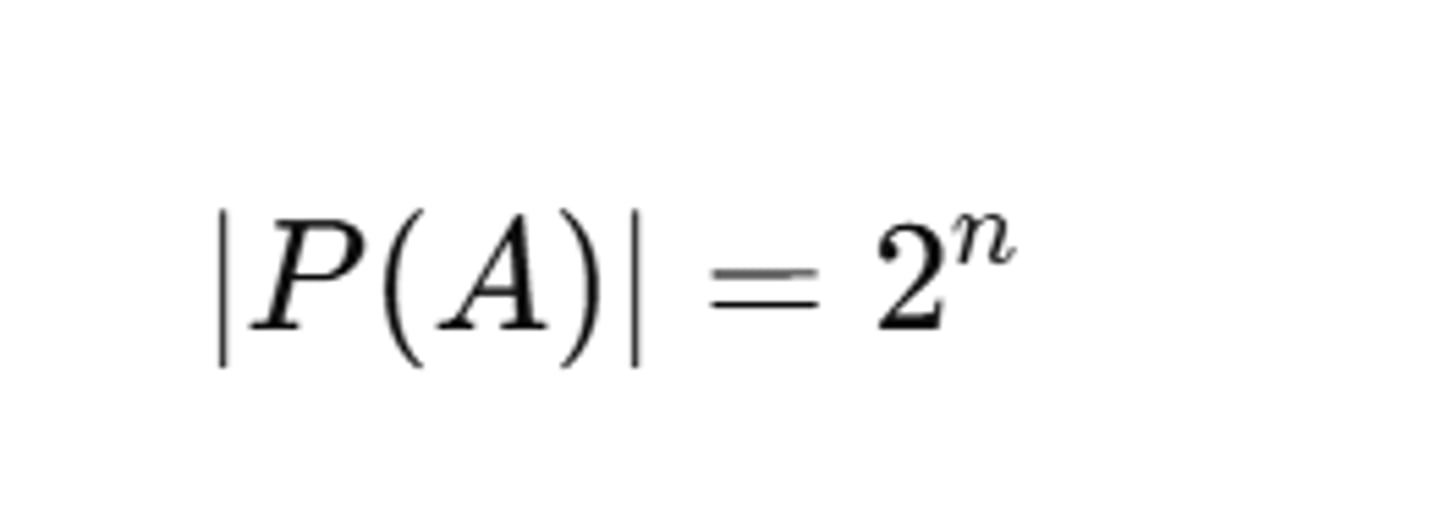
what does ∅ represent

The empty set, a set with no elements

What does ⊆ mean

Subset of." A⊆B means every element of A is in B.

What does ∈ mean in set theory

"Element of." 3 ∈ {1,2,3}

If A={1,2}, what is P(A) <= powerset of A

P(A)={∅,{1},{2},{1,2}}

What is the Cartesian Product of two sets?

set of all possible ordered pairs of A and B

an ordered pair is (x,y)

if x∈A and y∈B

AxB= {x: x= (a,b) | a∈A, b∈B,

null if A is null and/or B is null}

If A={1,2,3,4,5,6} what is |P(A)| =?

cardinality 2^6 = 64

An ordered n-tuple is

sequence of n elements written in a specific order inside parentheses:

(a_1, a_2, a_3,a_n)

The order matters.

Repetition of elements is allowed.

(a1,a2,…,an)≠(b1,b2,…,b) unless each a_n =a_n

Given A={1,2,3} B={4,5}

what is AXB

BXA

A×B={(1,4),(1,5),(2,4),(2,5),(3,4),(3,5)}

B×A={(4,1),(4,2),(4,3),(5,1),(5,2),(5,3)}

AxB/= BxA

order of element matters

if |A| =4 and |B| =2 and |C|=2

how many elements are in

|A| x |B| x |C| ?

16 elements

a={1,2}

b={3,4}

c={5}

axbxc?

a×b×c={(1,3,5),(1,4,5),(2,3,5),(2,4,5)}

4 elements

unary relation

A unary relation relates elements of A to itself and is a subset R1⊆A×A

How is a unary relation usually described?

By a predicate that defines the relation (e.g., <, ≤, =, >, ≥, "older than," "bigger than," etc.).

What is a binary relation?

A binary relation R relates elements of set A to elements of set B and is a subset R⊆A×B

How can a relation R be written

a set of ordered pairs

ex:

If A={1,2} and B={3,4}, then a relation R could be

R={(1,3),(2,4)}

domain of R

dom R={x∣x∈A and (x,y)∈R for some y∈B}

How are relations used in defining a hierarchy of system requirements?

Relations are used to trace requirements to functions (binary relations) of systems, subsystems, components, etc. Examples include "decompose of" and "incorporate."

What is the range of a relation R?

ran R={y∣y∈B and (x,y)∈R for some x∈A}

Let R be a relation from A to B, where

A={1,3,5,7}, B={1,3,5}

and R is defined as "x < y"

R={(1,3),(1,5),(3,5)}

cartesian product :

A×B={(1,1),(1,3),(1,5),(3,1),(3,3),(3,5),(5,1),(5,3),(5,5),(7,1),(7,3),(7,5)} ; but R only has valid pairs where the first element is less than the second

How is the dynamic behavior of systems modeled

function

What is the relationship progression between sets, relations, and functions?

Sets → Relations → Functions.

Define a function f:A→B

A function maps every element of A(domain) to one and only one element of B(range).

If (a,b)∈f(a,b)

what does that mean?

b is the image of element a under f.

Can a function map elements of A onto itself?

Yes, a function can map A→A

A function f from A to B is a relation such that... (list conditions).

1) dom f=A

- f is defined for every element of A, a∈A

- For each a∈A, there exists some b∈B such that (a,b)∈f

2) If (a,b)∈f and (a,c)∈f then b=c

- This means f is single values

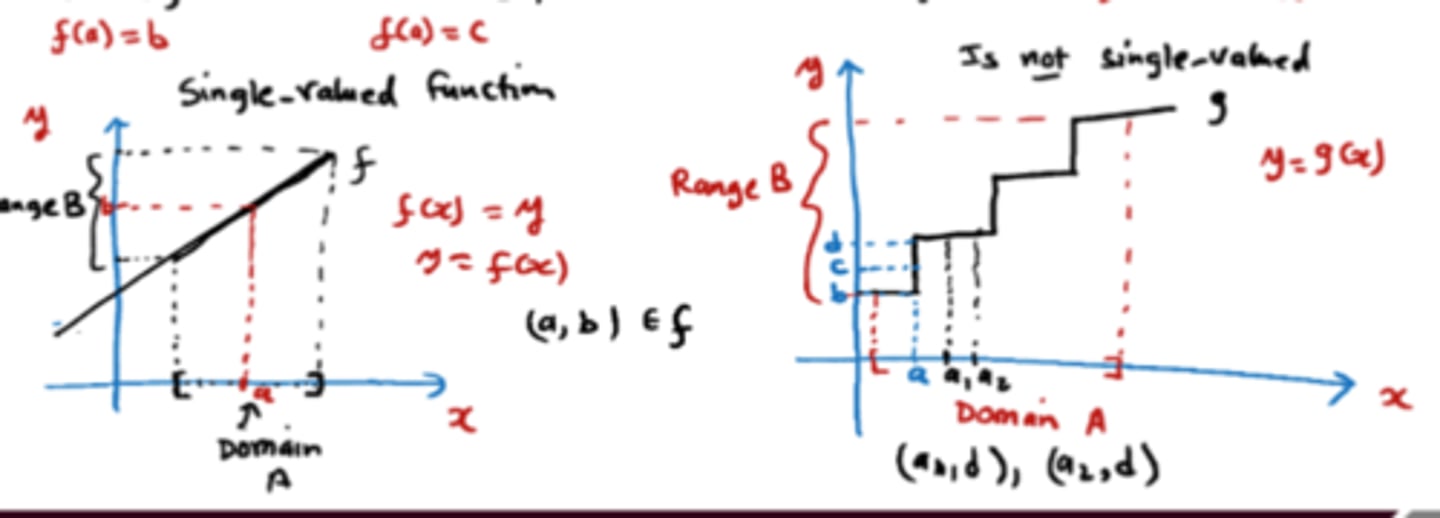
What is the difference between a single-valued function and a non-single-valued relation?

- Single-valued: each a in the domain maps to exactly one b in the range.

- Not single-valued: an a in the domain maps to more than one b

What is the notation for the set of functions from A to B?

F(A,B)

What is the definition of F(A,B)

The set of all functions |F⊆A×B

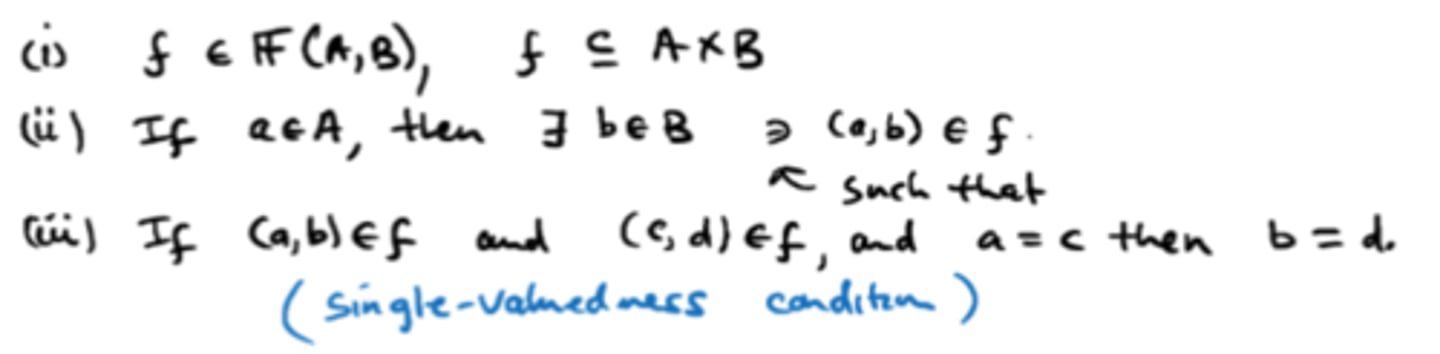
What is the single-valuedness condition for functions?

If (a,b)∈f(a,b) and (a,d)∈f(a,d) , then b=d

When is a function injective (one-to-one)?

If (a,b)∈f(a,b) and (c,b)∈f(c,b) ⇒ a=c

When is a function surjective (onto)?

If range(f) = B; i.e., for every b∈B there exists a∈Aa such that f(a)=b

When is a function bijective?

If it is both injective and surjective

What makes a function bijective?

The inverse f^{-1}exists, is single-valued, and maps every element of B to some element of A.

What is the definition of function composition?

If f∈𝓕(A,B) and g∈𝓕(B,C), then f ∘ g is defined as f∘g={(a,c):a∈A,c∈C,b∈B⇒(a,b)∈f,(b,c)∈g}

What does function composition mean in words?

Applying one function after another (first g, then f).

Let A={1,2,3},B={11,12,13},C={21,22,23}

f={(1,11),(2,12),(3,13)},

g={(11,21),(12,22),(13,23)}

what is f∘g and is the composition of functions still a function

f∘g={(1,21),(2,22),(3,23)}

yes